A bullet of mass 0.25 kg is fired with velocity 302m/s into a block of wood of mass 37.5kg.It gets embedded into it. The block is resting on a long block and the horizontal surface on which it is placed. The coefficient of friction between and is 0.5. Find the displacement of on and the common velocity of and . Mass = 12.5kg.
The correct Answer is:
Step by step video, text & image solution for A bullet of mass 0.25 kg is fired with velocity 302m/s into a block of wood of mass 37.5kg.It gets embedded into it. The block m_(1) is resting on a long block and the horizontal surface on which it is placed. The coefficient of friction between m_(1) and m_(2) is 0.5. Find the displacement of on and the common velocity of m_(1) and m_(2). Mass m^(2)= 12.5kg. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Advance McQ
Explore 20 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
A bullet of mass 0.1Kg moves with velocity 10ms it strikes a block and comes to rest after travels 0.5 m inside block. Find retardation of bullet
View SolutionA bullet of mass 0.1Kg moves with velocity 10ms it strikes a block and comes to rest after travels 0.5 m inside block. Find retardation of bullet
View Solution
Knowledge Check
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)MD12mv2(M+m)mA bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A block of mass 1kg lies on a horizontal surface in a turck, the coefficient of static fricition between the block and the surface is 0.6, what is the force of fricition on the block. If the acceleration of the truck is 5m/s2.
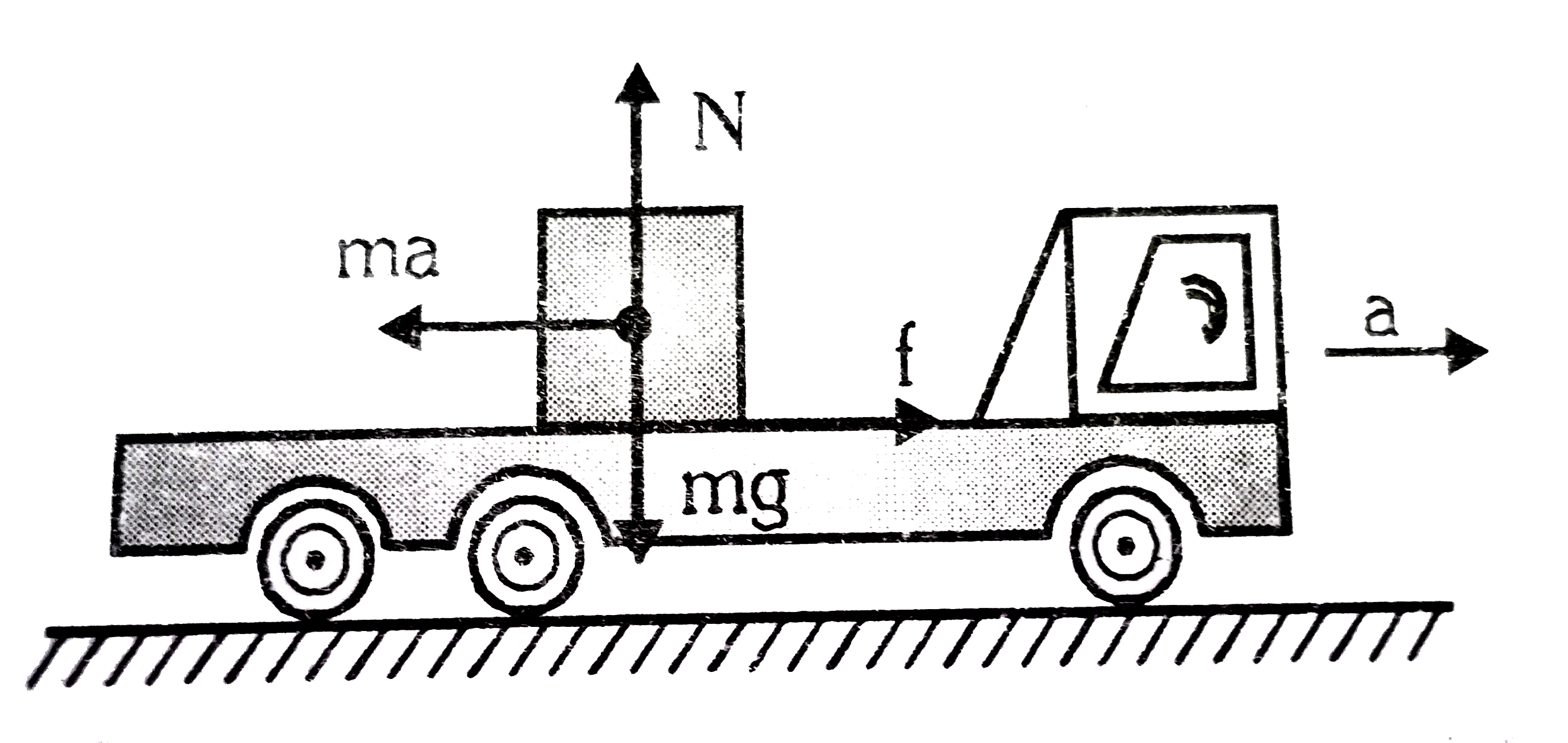
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View SolutionA block of mass m = 1 kg is placed over a plank Q of mass M = 6 kg, placed over a smooth horizontal surface as shown in figure. Block P is given a velocity v=2m/s2 to the right. If the coefficient of friction between P and Q is μ=0.3. Find the acceleration of Q relative to P.
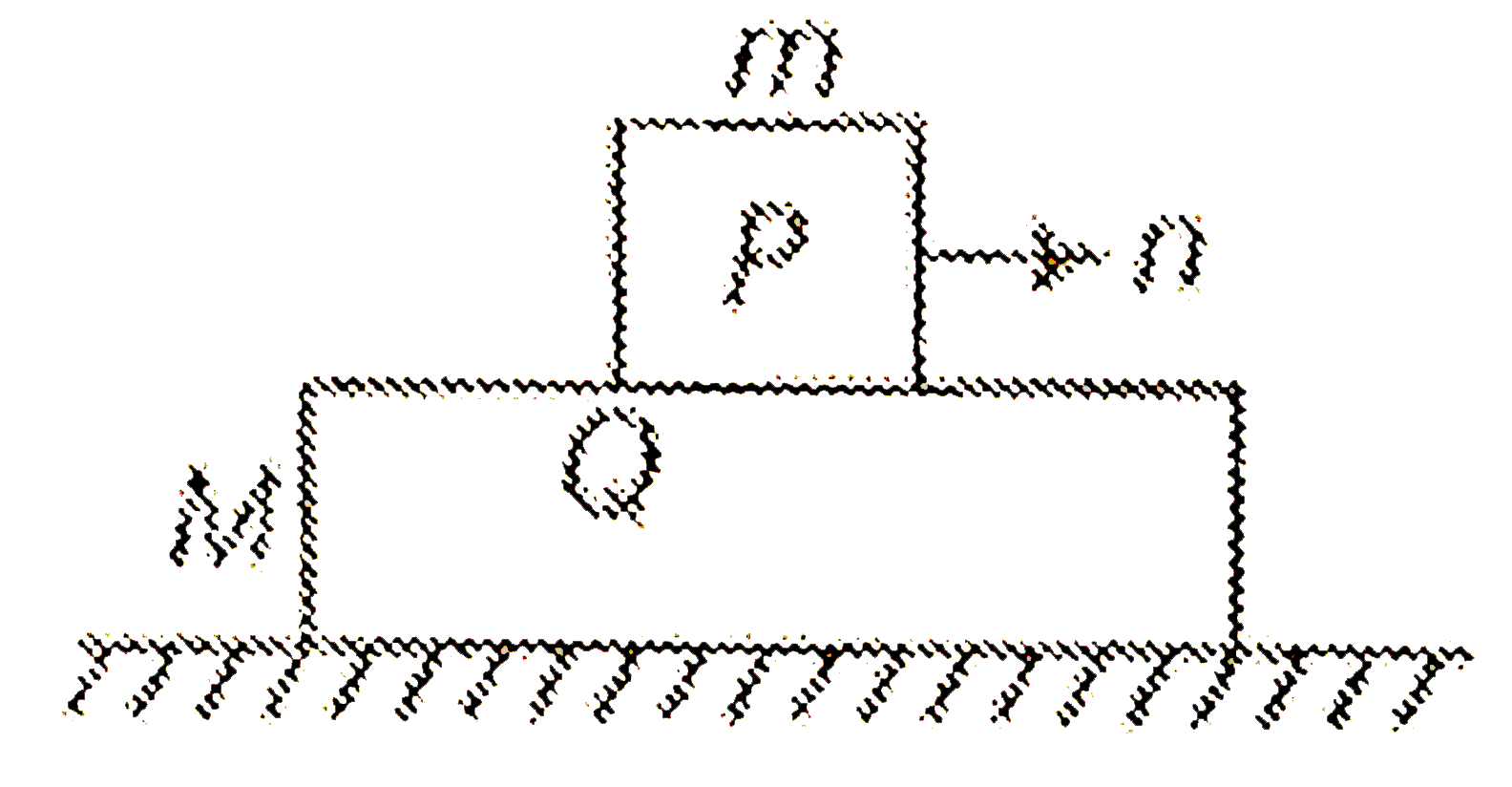
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View Solution

