A charged particle of unit mass and unit charge moves with velocity $\to v = (8 ˆ i + 6 ˆ j) m s^{- 1}$ in magnetic field of $\to B = 2 ˆ k T$ . Choose the correct alternative (s).

The path of particle may be $x^{2} + y^{2} - 4 x - 21 = 0$

The path of particle may be $x^{2} + y^{2} = 25$

The path of particle may be $y^{2} + z^{2} = 25$

Time period of particle will be 3.14s

Video Solution

Answer

Step by step video & image solution for A charged particle of unit mass and unit charge moves with velocity vecv=(8hati+6hatj)ms^-1 in magnetic field of vecB=2hatkT. Choose the correct alternative (s). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A charged particle of specific charge $α$ moves with a velocity $\to v = v_{0} ˆ i$ in a magnetic field $\to B = \frac{B_{0}}{\sqrt{2}} (ˆ j + ˆ k)$ . Then (specific charge=charge per unit mass)
Apath of the particle is a helix
Bpath of the particle is circle
Cdistance moved by the particle in time $t = \frac{π}{B_{0} α} i s \frac{π v_{0}}{B_{0} α}$
Dvelocity of the particle after time $t = \frac{π}{B_{0} α} i s (\frac{v_{0}}{2} ˆ j + \frac{v_{0}}{2} ˆ j)$
Question 2 - Select One
A charge particle moves with velocity $\to V = A ˆ i + D ˆ j$ magnetic field . $\to B = A ˆ i + D ˆ j$ The force acting on the particle has magnitude .F Then,
AF = 0 , if aD = dA
BF = 0 , if aD = -dA
CF = 0 , if aA = -dD
D $F \propto {(a^{2} + b^{2})}^{1 / 2} \times {(A^{2} + D^{2})}^{1 / 2}$
Question 3 - Select One
A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

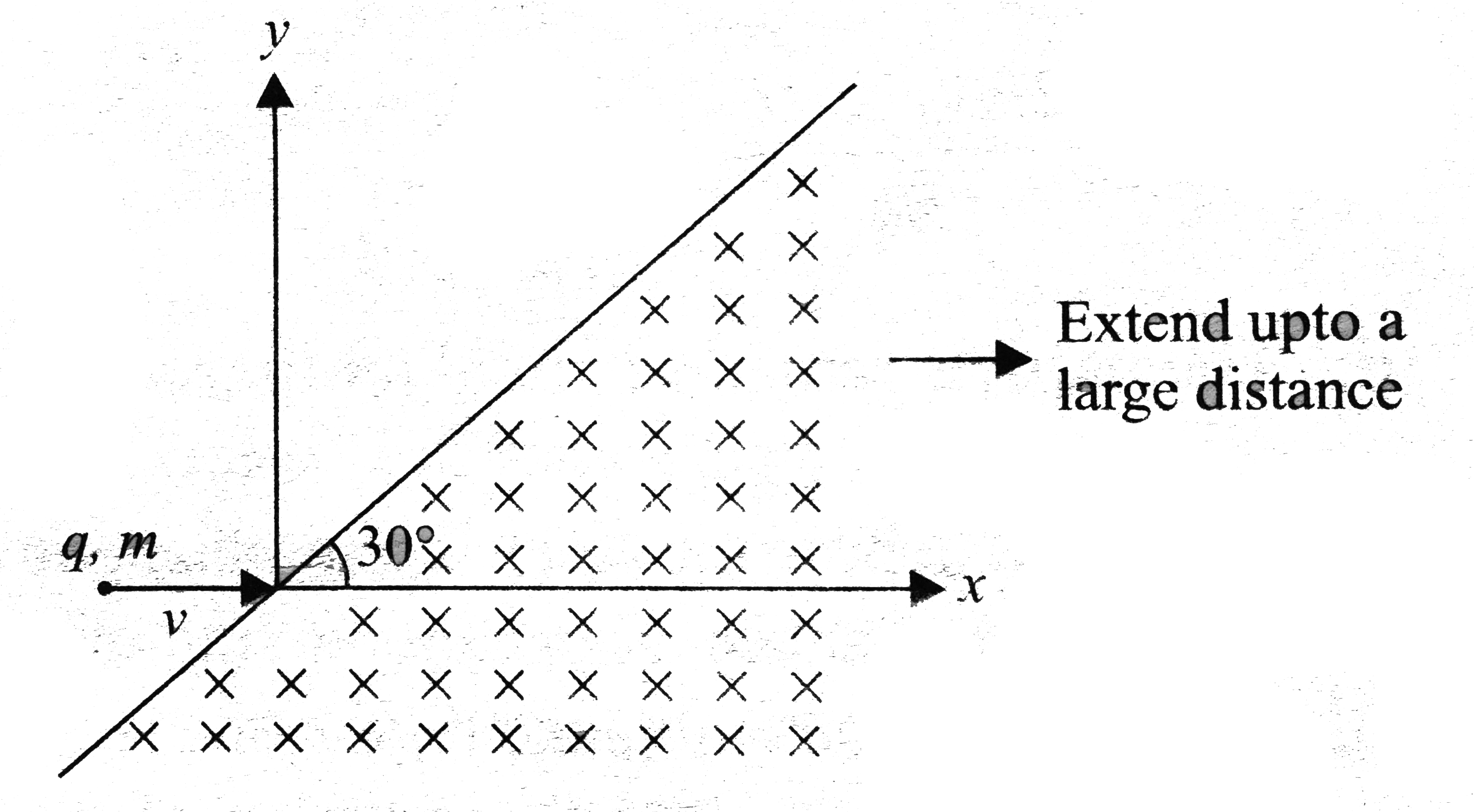AVelocity of the particle when it comes out form the magnetic field is $\to v - v {cos 60}^{\circ} ˆ i + v {sin 60}^{\circ} ˆ j$
BTime for which the particle was in magnetic field is $\frac{π m}{3 q B}$
CDistance travelled in magnetic field is $\frac{π m v}{3 q B}$
DNone of these

PHYSICS GALAXY - ASHISH ARORA-MAGNETIC EFFECTS OF CURRENT AND MAGNETISM-Advance MCQ

Home
Ask Doubt
Profile

A charged particle of unit mass and unit charge moves with velocity →v=(8ˆi+6ˆj)ms−1 in magnetic field of →B=2ˆkT. Choose the correct alternative (s).

Topper's Solved these Questions

Similar Questions

Knowledge Check

A charged particle of specific charge α moves with a velocity →v=v0ˆi in a magnetic field →B=B0√2(ˆj+ˆk). Then (specific charge=charge per unit mass)

A charge particle moves with velocity →V=Aˆi+Dˆj magnetic field . →B=Aˆi+Dˆj The force acting on the particle has magnitude .F Then,

A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

PHYSICS GALAXY - ASHISH ARORA-MAGNETIC EFFECTS OF CURRENT AND MAGNETISM-Advance MCQ

A charged particle of unit mass and unit charge moves with velocity $\to v = (8 ˆ i + 6 ˆ j) m s^{- 1}$ in magnetic field of $\to B = 2 ˆ k T$ . Choose the correct alternative (s).

A charged particle of specific charge $α$ moves with a velocity $\to v = v_{0} ˆ i$ in a magnetic field $\to B = \frac{B_{0}}{\sqrt{2}} (ˆ j + ˆ k)$ . Then (specific charge=charge per unit mass)

A charge particle moves with velocity $\to V = A ˆ i + D ˆ j$ magnetic field . $\to B = A ˆ i + D ˆ j$ The force acting on the particle has magnitude .F Then,