A bead can slide on a smooth straight wire and a particle of mass attached to the bead by a light string of length . The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass then when the string makes an angle with the wire, the bead will have slipped a distance.

The correct Answer is:
Step by step video, text & image solution for A bead can slide on a smooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a distance. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
Similar Questions
A particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
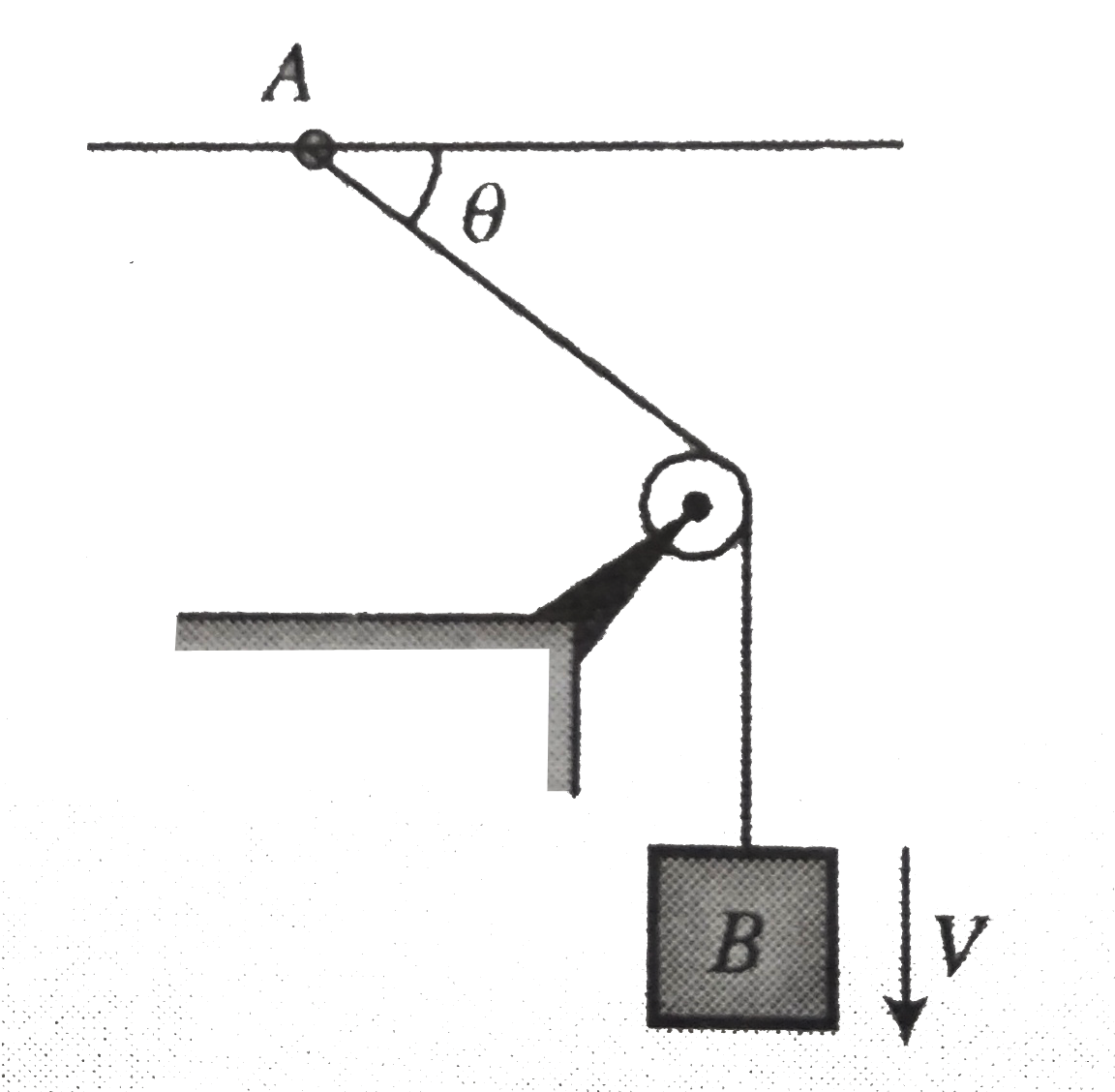
View Solution
Knowledge Check
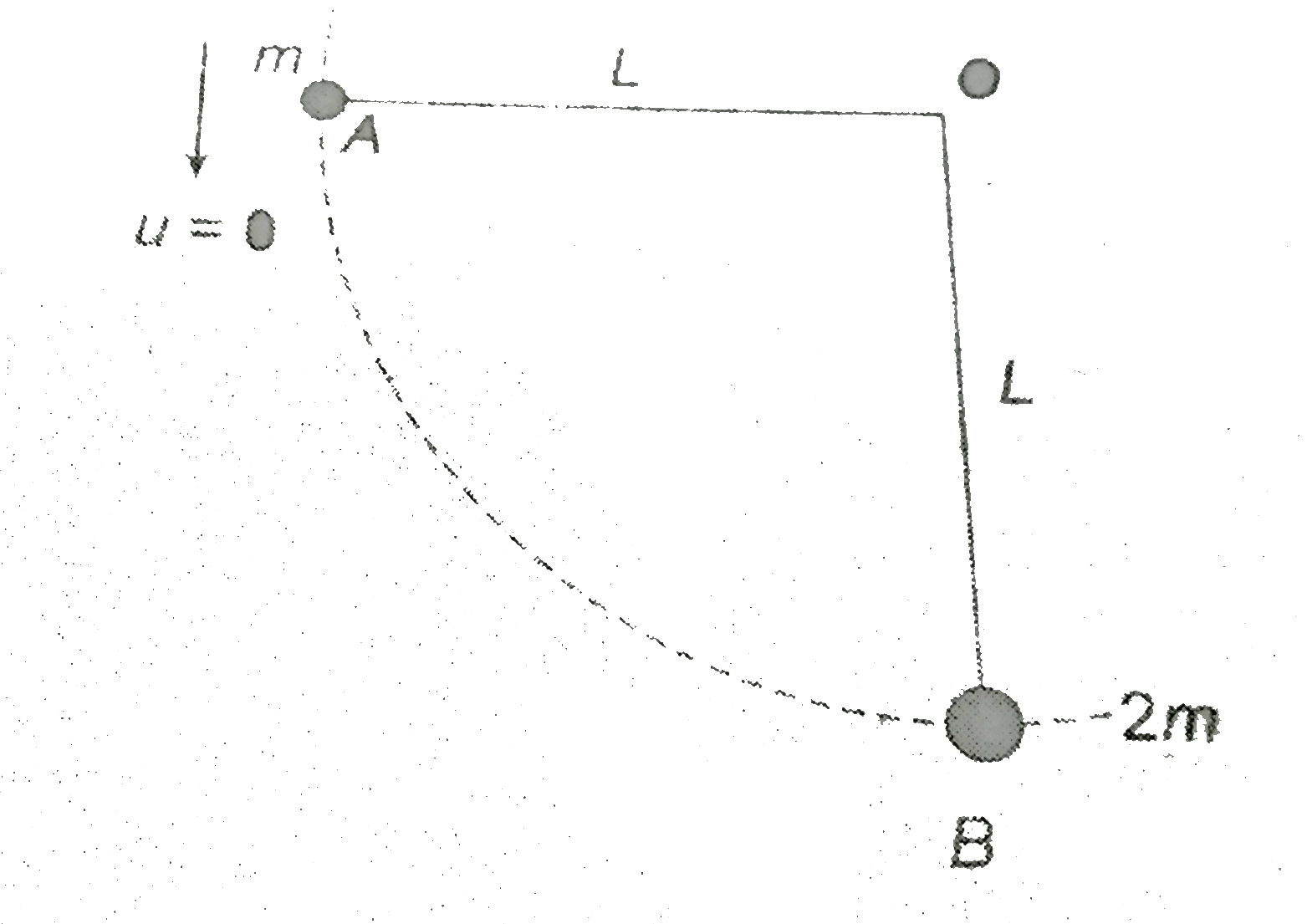
A bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a dsitance.
 AL(1−cosθ)B(L2)(1−cosθ)C(L3)(1−cosθ)D(L6)(1−cosθ)
AL(1−cosθ)B(L2)(1−cosθ)C(L3)(1−cosθ)D(L6)(1−cosθ)A body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
Amu2lBmu2l+mgcosθCmu2l+mg(2cosθ−3)Dmu2l+mg(3cosθ−2)A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle such that θ is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
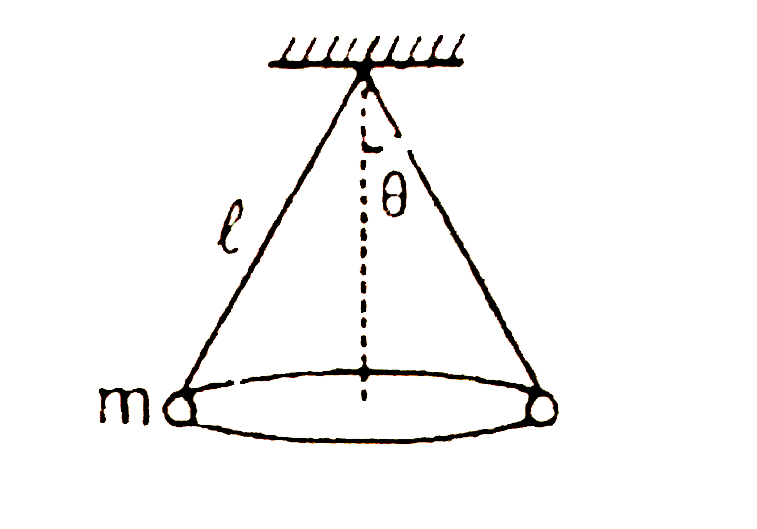
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)
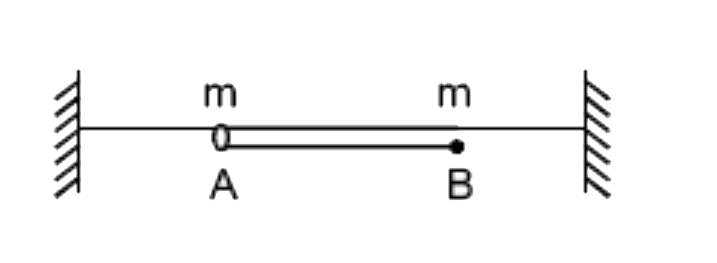
View SolutionA particle of mass m is attached to a string of length L and given velocity √10hL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (a) (i) lowest position (ii) highest position, (b) when the string makes an angle 60∘ with (i) lower vertical and (ii) upper vertical.
View Solution
