A cannon and a supply of cannon balls are inside a sealed rail road car. The cannon fires to the right, the car recoils to the left. The canon balls remain in the car after hitting the far wall. Show that no matter how the cannon balls are fired, the rail road car cannot travel more than L. assuming it starts from rest.

Step by step video, text & image solution for A cannon and a supply of cannon balls are inside a sealed rail road car. The cannon fires to the right, the car recoils to the left. The canon balls remain in the car after hitting the far wall. Show that no matter how the cannon balls are fired, the rail road car cannot travel more than L. assuming it starts from rest. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTION, FREE BODY DIAGRAMBook:NN GHOSHChapter:LAWS OF MOTION, FREE BODY DIAGRAMExercise:Exercise (A)
Explore 27 Videos
- KINETIC THEORY OF GASESBook:NN GHOSHChapter:KINETIC THEORY OF GASESExercise:All Questions
Explore 24 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBook:NN GHOSHChapter:MOMENT, TORQUE, EQUILIBRIUM OF BODIESExercise:Exercises
Explore 33 Videos
Similar Questions
Two 20kg cannon balls are chained together and fired horizontally with a velocity of 200m/s from the top of a 30m wall. The chain breaks during the flight of the cannon balls and one of them strikes the ground at t=2s, at a distance of 250m from the foot fo the wall, and 5m to the right of line of fire determine the position of the other cannon ball at that instant Neglect the resistance of air.

View SolutionA car starts from rest on a half kilometer long bridge. The coefficiet of friction between the tyre and the road is 1.0. Show that one cannot drive thrugh the bridge in less than 10 s.
View Solution
Knowledge Check
A cannon-ball is fired with a speed 50m/sec with respect to ground from one end of a stationary railroad car which rests on a smooth track. The ball collides with opposite wall and stops. How much distance did the railroad car cover just before the collision? Given that the ratio of the mass of the ball to that of the railroad car is 1/99 and the length of the car is 50m
 A2mB12mC0mDcannot be calculated from acts
A2mB12mC0mDcannot be calculated from actsA physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement.
The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as Lx, and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity Vx and of widht D and he is swimming in direction perpendicular to the river flow with velocity Vy relation to river, assuming no use of directed lengths, the quantities of interest are then Vx,Vy both dimensioned as LT , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S∝VaxVbyDc
Or dimensionally L=(LT)a+b×(L)c from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then Vx will be dimensioned as LxT,VyasLyT,SasLx and DasLy. The dimensional equation becomes : Lx=(LxT)a(LyT)b(Ly)c and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent.
From the concept of directed dimension what is the formula for a range (R) of a cannon ball when it is fired with vertical velocity component Vy and a horizontal velocity component Vx, assuming it is fired on a flat surface. [Range also depends upon acceleration due to gravity , g and k is numerical constant]AR=k(VxVy)gBR=k(Vx)2gCR=k(Vx)3VygDR=k(Vy)3VxgA cannon is fixed with a smooth massive trolley car at an angle θ as shown in the figure.The trolley car slides from rest down the inclined plane of angle of inclination β.
The muzzle velocity of the shell fired at t=y0 from the cannon is u,such that the shell moves perpendicular to the inclined just after the firing.
the difference in range of the shell relative to the trolley car and ground is:
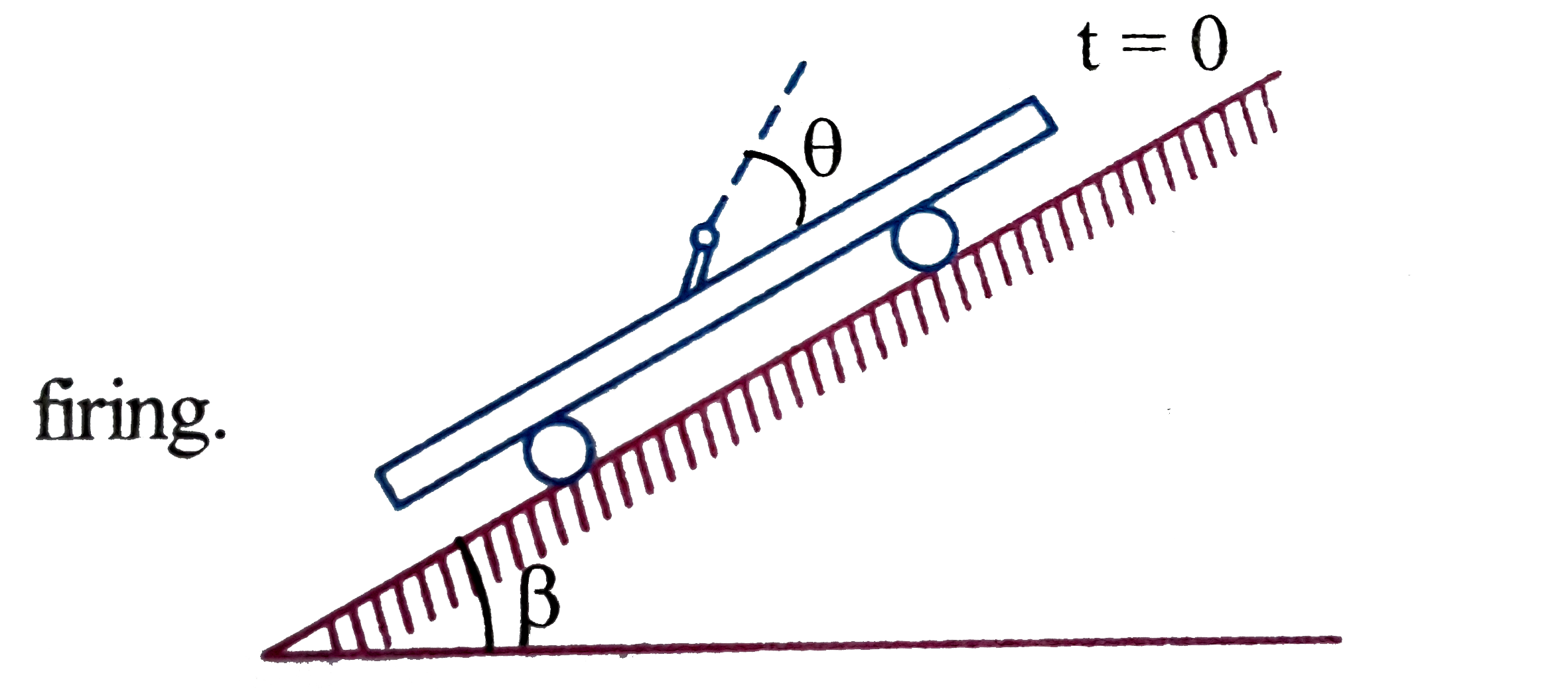 Au2sin2θgcosβBu2cosθ2gsinβCu2sinθsinβ2gD2U2sinθcos(θ−β)gcos2g
Au2sin2θgcosβBu2cosθ2gsinβCu2sinθsinβ2gD2U2sinθcos(θ−β)gcos2g
A car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100m/s at an angle 30∘ with the horizontal. The first cannon hall hits the stationary carriage after a timet0 and sticks to it. Determine t0.
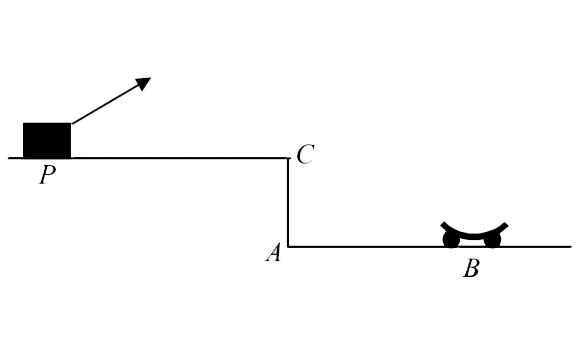
At t0, the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout. If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact?
View SolutionA car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100m/s at an angle 30∘ with the horizontal. The first cannon hall hits the stationary carriage after a timet0 and sticks to it. Determine t0.

At t0, the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout. If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact?
View SolutionAn isolated rail car of mass M is moving alonga straight, frictionless track at an initial speed v0. The car is passing under a bridge when a crate filled with N bowling balls, each of mass m, is dropped from the bridge into the bed of the rail car. the crate splits open and the bowling balls bounce around inside the rail car, but none of them fall out.
(B).What is the average speed of the rail car + bowling balls system some time after the collision?
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
View SolutionA man standing on a long rail road car throws a ball vertically upward with speed 20m/s. The car starts from rest and moves with acceleration 2m/s2. How far behind the man will the ball fall on the car ?
View Solution

