Find the locus of points where the electric field (resultant ) will always have a bearing of 45∘ with the axis of the dipole .
The correct Answer is:A st. line at 29∘18' with the axis
Step by step video, text & image solution for Find the locus of points where the electric field (resultant ) will always have a bearing of 45^(@) with the axis of the dipole . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the locus of points where the electric field due to a dipole is (i) perpendicular to its axis , (ii) anti-parallel to the axis .
[Hint : tanα=tanθ2]
View SolutionFind the locus of the points where the intensity of the magnetic field due to a magnetic dipole will be perpendicular to its axis.
View Solution
Knowledge Check
For an electric dipole potential & electric field
Acan have same magnitude for a point at a distance less than 2 meterBcan have same magnitude fo a point at distacnes greater than 2 meterCcan never be equalDcan never be predictedAt a point on the axis of an electric dipole
Athe electric field E is zeroBthe electric potential V is zeroCboth E and V are zeroDneither E nor V is zeroElectric field due to an electric dipole is
Aspherically symmetricBcylindrical symmetricCasymmetricDnone of the above
There is one short electric dipole placed on a plane. A straight line is drawn on this plane passing through the centre of electric dipole making an angle θ with the axis of dipole. A point P is selected on this line at a distance ten times the length of electric dipole from centre of electric dipole. Electric field intensity at the point P makes an angle α with the axis of electric dipole . What will be the magnitude of tanθtanα ?

View SolutionThere is one short electric dipole placed on a horizontal plane. A circle is drawn assuming centre of dipole as centre of circle and plane of the circle is perpendicular to the axis of electric dipole. Thế number of points on this circle where electric field intensity due to electric dipole is perpendicular to the axis of dipole.

View SolutionThe electric field due to a dipole at a distance on its axis is
View SolutionElectric field due to an electric dipole is
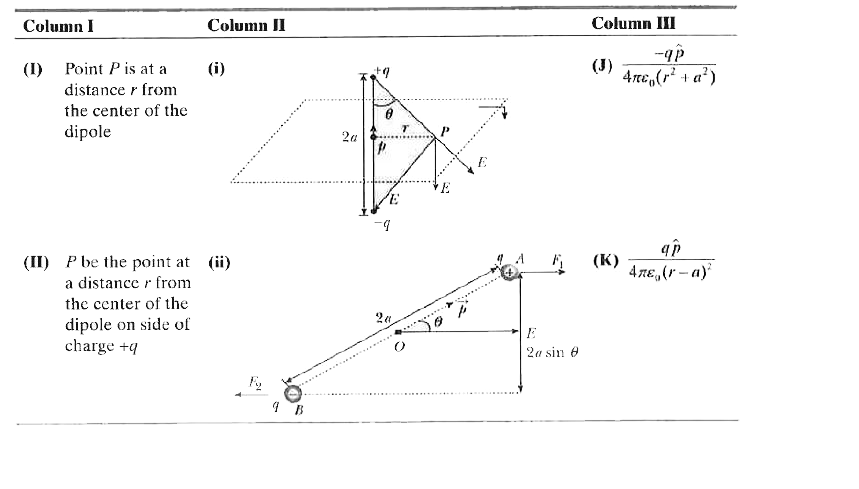
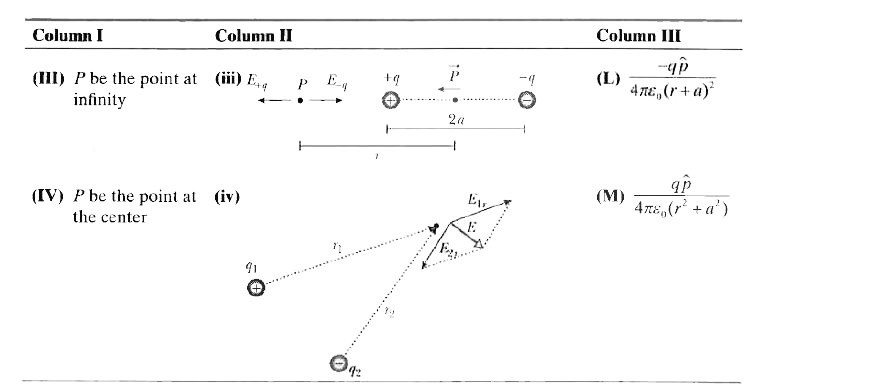
View SolutionAn electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
When point P lies on the axis of the electric dipole, electric field due to -q is ?
View Solution

