Two circular coils A and B with their centres lying on the same axis have differents in the same sence. The coil B lies exacity midway between coil A and the point P. The magnetic field at point P due to coils A and B is B1 and B2 respectively.
B1>B2
B1<B2
B1B2=2
B1B2=12
The correct Answer is:C, D
To solve the problem of determining the relationship between the magnetic fields B1 and B2 at point P due to two circular coils A and B, we can follow these steps:
Step 1: Understand the Configuration
- We have two circular coils, A and B, with their centers aligned on the same axis.
- Coil B is positioned exactly midway between coil A and point P.
Step 2: Define the Magnetic Fields
- Let B1 be the magnetic field at point P due to coil A.
- Let B2 be the magnetic field at point P due to coil B.
Step 3: Use the Formula for Magnetic Field
The magnetic field B at a point along the axis of a circular coil is given by the formula:
B=μ0nIR22(R2+x2)3/2
where:
- μ0 is the permeability of free space,
- n is the number of turns in the coil,
- I is the current flowing through the coil,
- R is the radius of the coil,
- x is the distance from the center of the coil to the point where the field is being measured.
Step 4: Apply the Formula to Both Coils
1. For coil A:
- Let the distance from coil A to point P be dA.
- The magnetic field B1 at point P due to coil A is:
B1=μ0nAIAR2A2(R2A+d2A)3/2
2. For coil B:
- Since coil B is midway, the distance from coil B to point P is dB=dA2.
- The magnetic field B2 at point P due to coil B is:
B2=μ0nBIBR2B2(R2B+d2B)3/2
Step 5: Establish the Relationship Between B1 and B2
- Since both coils are aligned and have the same angle at point P, we can set up a ratio:
B1B2=μ0nAIAR2A2(R2A+d2A)3/2μ0nBIBR2B2(R2B+d2B)3/2
- This simplifies to:
B1B2=nAIAR2A(R2B+d2B)3/2nBIBR2B(R2A+d2A)3/2
Step 6: Solve for the Ratio
- If we assume that the coils have the same number of turns and the same current, we can simplify further.
- After simplification, we find that:
B1B2=12
- Thus, we conclude that:
B1=12B2
Final Answer
The relationship between the magnetic fields at point P due to coils A and B is:
B1:B2=1:2
- We have two circular coils, A and B, with their centers aligned on the same axis.
- Coil B is positioned exactly midway between coil A and point P.
- Let B1 be the magnetic field at point P due to coil A.
- Let B2 be the magnetic field at point P due to coil B.
The magnetic field B at a point along the axis of a circular coil is given by the formula:
B=μ0nIR22(R2+x2)3/2
where:
- μ0 is the permeability of free space,
- n is the number of turns in the coil,
- I is the current flowing through the coil,
- R is the radius of the coil,
- x is the distance from the center of the coil to the point where the field is being measured.
1. For coil A:
- Let the distance from coil A to point P be dA.
- The magnetic field B1 at point P due to coil A is:
B1=μ0nAIAR2A2(R2A+d2A)3/2
- Since coil B is midway, the distance from coil B to point P is dB=dA2.
- The magnetic field B2 at point P due to coil B is:
B2=μ0nBIBR2B2(R2B+d2B)3/2
- Since both coils are aligned and have the same angle at point P, we can set up a ratio:
B1B2=μ0nAIAR2A2(R2A+d2A)3/2μ0nBIBR2B2(R2B+d2B)3/2
- This simplifies to:
B1B2=nAIAR2A(R2B+d2B)3/2nBIBR2B(R2A+d2A)3/2
- If we assume that the coils have the same number of turns and the same current, we can simplify further.
- After simplification, we find that:
B1B2=12
- Thus, we conclude that:
B1=12B2
The relationship between the magnetic fields at point P due to coils A and B is:
B1:B2=1:2
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Subjective type
Explore 11 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
Two circular coils X and Y, having equal number of turns and carrying currents in the same sense, subtend same solid angle at point O. If the smaller coil X is midway between O and Y and if we represent the magnetic induction due to bigger coil Y at O as By and the due to smaller coil X at O as Bx,then find the ratio Bx/By.

View SolutionTwo circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in the coil B? Give reason.
View Solution
Knowledge Check
The magnetic field at a point P due to a current carrying coil as shown in figure is
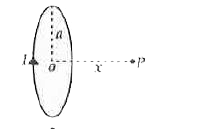 Aμ04π1a2Bμ04πlax(x2−a2)2Cμ04π2πla2x2Dμ04π2πla2(x2+a2)3/2
Aμ04π1a2Bμ04πlax(x2−a2)2Cμ04π2πla2x2Dμ04π2πla2(x2+a2)3/2Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes
AAre parallel to each otherBAre at 60∘ to each otherCAre at 45∘ to each otherDAre perpendicular to each otherA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
A√2RB√3RC2RD3R
Two circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in the coil B? Give reason.
View SolutionTwo circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in the coil B? Give reason.
View SolutionTwo circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in the coil B ? Give reason.
View SolutionTwo circular coils A and B are placed close to each other. If the current in the coil A is changed, will some current be induced in the coil B? Give reason.
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View Solution

