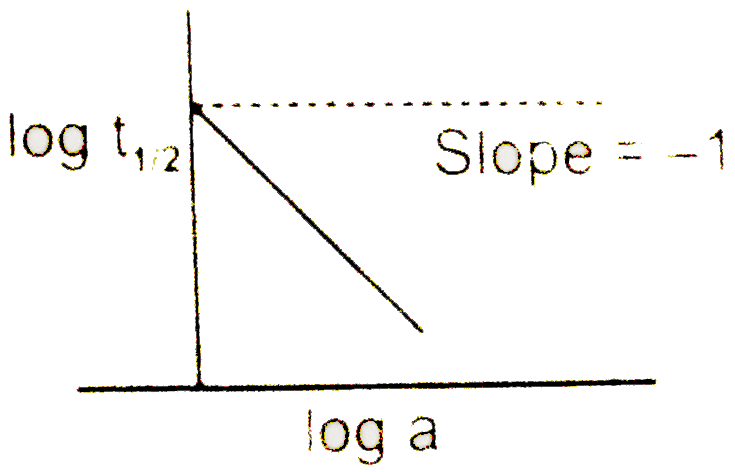
A graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
−d[A]dt=K
−d[A]dt=K[A]
−d[A]dt=K[A]2
−d[A]dt=K[A]3
The correct Answer is:C
Step by step video, text & image solution for A graph between log t_((1)/(2)) and log a (abscissa), a being the initial concentration of A in the reaction For reaction AtoProduct, the rate law is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)
2 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)
3 Videos
- SURFACE CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level 3 - Assertion - Reason Type Questions
1 Video
Similar Questions
Following is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 27∘C.

Find the order of reaction.
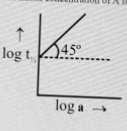
View SolutionFor a reaction A→ Products, a plot of logt12 ,versus log a is shown in figure. If the initial concentration of A is represented by a ,the order of the reaction is:-
View Solution
Knowledge Check
A graph between log t1/2 and log a (abscissa), a being the initial concentration of A in the reaction A → product, is depicted in the figure. The rate law is
 A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3
A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3A graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
 A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3
A−d[A]dt=kB−d[A]dt=k[A]C−d[A]dt=k[A]2D−d[A]dt=k[A]3Following is the graph between logT50 and loga (a= initial concentration) for a given reaction at 27∘C. Hence order is
 A0B1C2D3
A0B1C2D3
Following is the graph between log T50 and log a (a = initial concentration) for a given reaction at 27∘C.
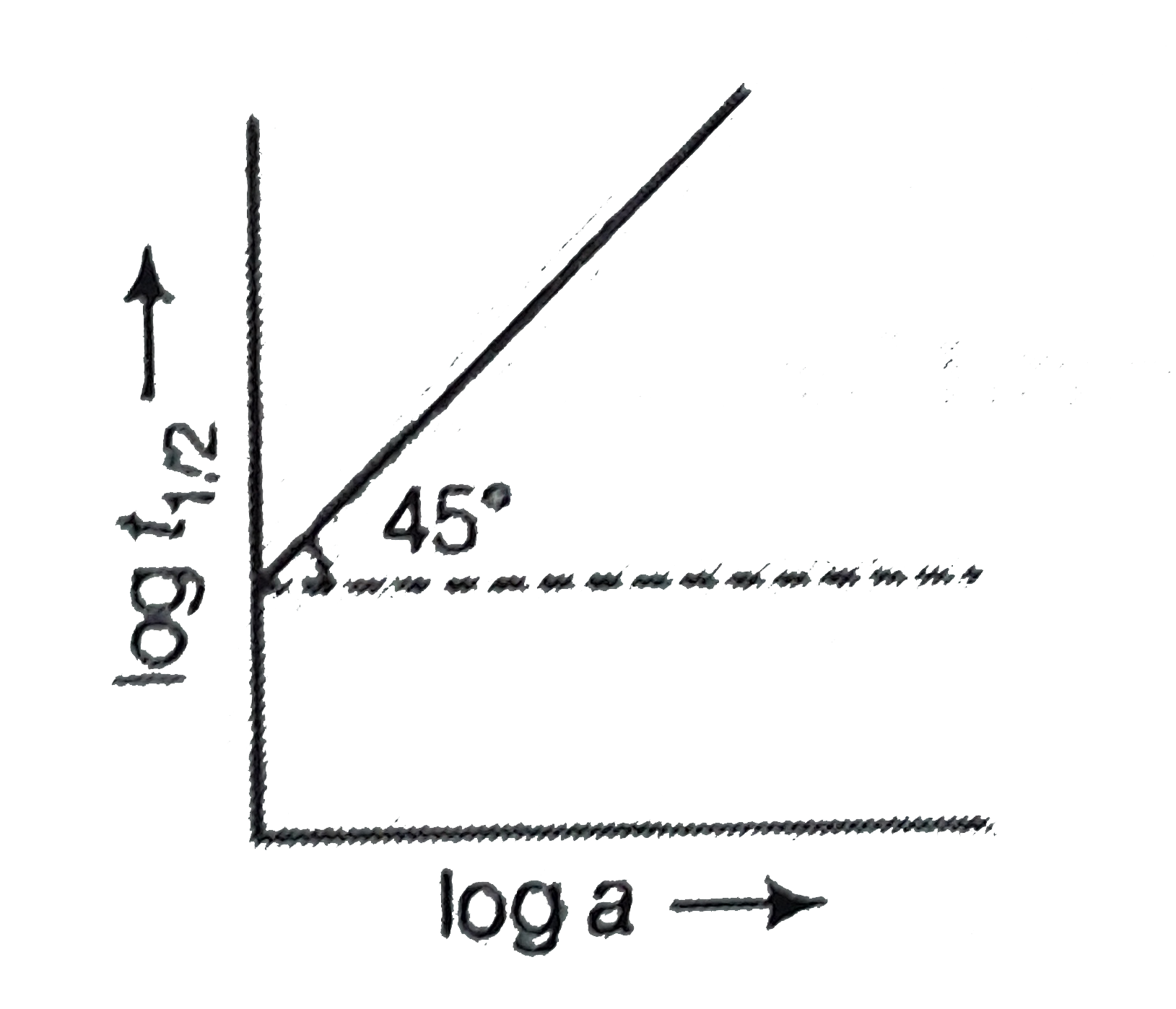
Hence, order is
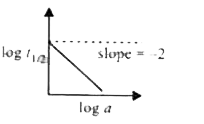
View SolutionThe graph between log t1/2 and log a at a given temperature is
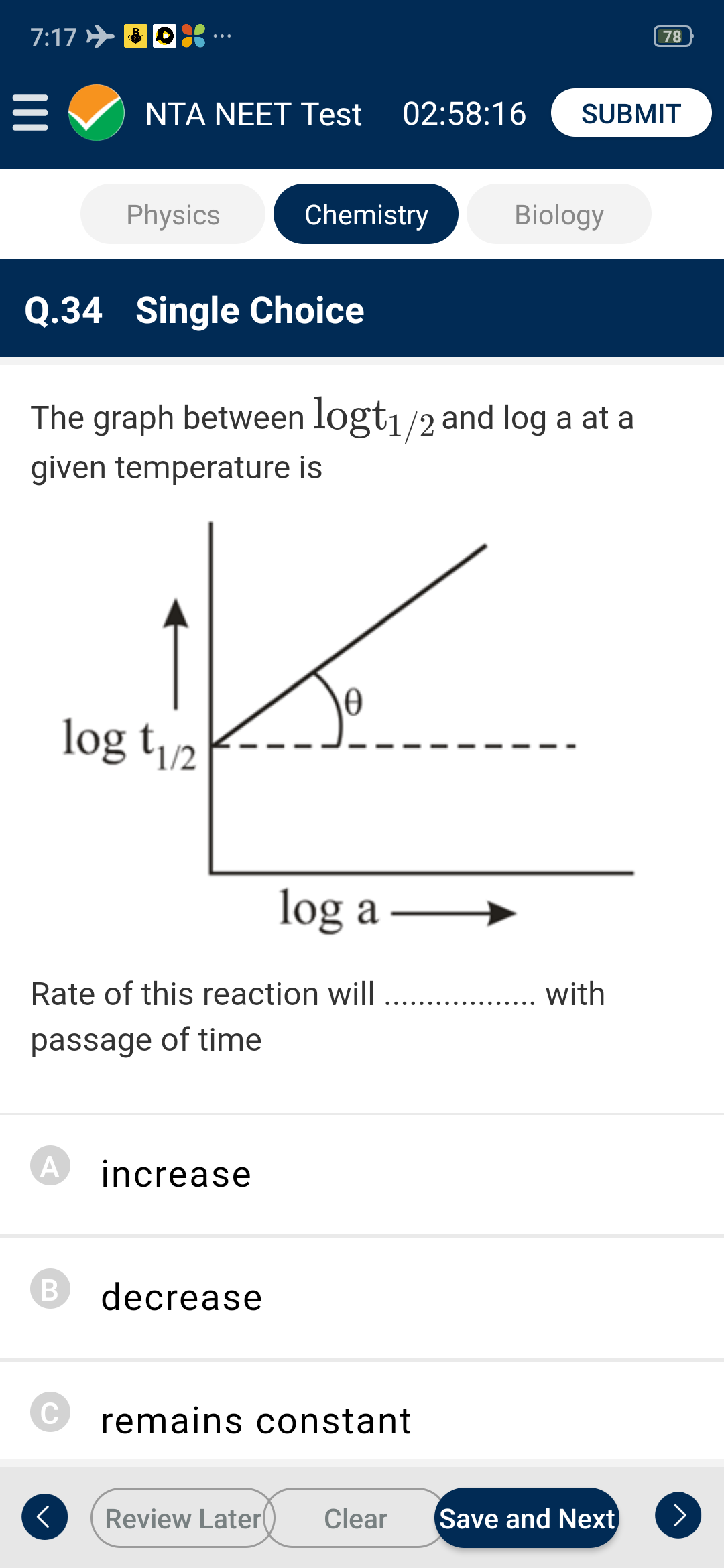
Rate of this reaction will …….with passage of time
View SolutionDerive an expression for the intergated rate equation for the first order reaction.
View SolutionPlotting log10t1/2 against log10[A0] (where A0 is the initial concentration of a reactant) for a fist order reaction the slope will be
View SolutionFor zero order reaction , t1/2 will be (A0 is the initial concentration , K is rate constant)
View Solution