Ionisation constant of a weak acid (HA) in terms of A∞m and Am is:
Ka=CA∞m(Am−A∞)
ka=CA2mA∞m(A00m−Am)
Ka=C(A∞m)2A∞m(A∞m−Am)
None of these
The correct Answer is:B
To derive the ionization constant (Ka) of a weak acid (HA) in terms of molar conductivity at infinite dilution (A_m^∞) and molar conductivity at some specific concentration (A_m), we can follow these steps:
1. Write the Dissociation Equation:
The dissociation of a weak acid (HA) can be represented as:
HA⇌H++A−
2. Define Initial and Equilibrium Concentrations:
Let the initial concentration of the acid be C. At equilibrium, if α is the degree of dissociation, the concentrations will be:
- (H+)=Cα
- (A−)=Cα
- (HA)=C(1−α)
3. Write the Expression for the Ionization Constant (Ka):
The ionization constant Ka is given by:
Ka=(H+)(A−)(HA)=Cα⋅CαC(1−α)=C2α2C(1−α)=Cα21−α
4. Relate Degree of Dissociation to Molar Conductivity:
The degree of dissociation α can be expressed in terms of molar conductivities:
α=AmA∞m
where Am is the molar conductivity at concentration C and A∞m is the molar conductivity at infinite dilution.
5. Substitute α into the Ka Expression:
Substitute the expression for α into the equation for Ka:
Ka=C(AmA∞m)21−AmA∞m
6. Simplify the Expression:
To simplify, let’s rewrite the denominator:
Ka=CA2mA∞2mA∞m−AmA∞m=CA2mA∞2m⋅(A∞m−AmA∞m)
This can be further simplified to:
Ka=CA2mA∞m(A∞m−Am)
Final Expression:
Thus, the ionization constant Ka of the weak acid (HA) in terms of molar conductivities is:
Ka=CA2mA∞m(A∞m−Am)
The dissociation of a weak acid (HA) can be represented as:
HA⇌H++A−
Let the initial concentration of the acid be C. At equilibrium, if α is the degree of dissociation, the concentrations will be:
- (H+)=Cα
- (A−)=Cα
- (HA)=C(1−α)
The ionization constant Ka is given by:
Ka=(H+)(A−)(HA)=Cα⋅CαC(1−α)=C2α2C(1−α)=Cα21−α
The degree of dissociation α can be expressed in terms of molar conductivities:
α=AmA∞m
where Am is the molar conductivity at concentration C and A∞m is the molar conductivity at infinite dilution.
Substitute the expression for α into the equation for Ka:
Ka=C(AmA∞m)21−AmA∞m
To simplify, let’s rewrite the denominator:
Ka=CA2mA∞2mA∞m−AmA∞m=CA2mA∞2m⋅(A∞m−AmA∞m)
This can be further simplified to:
Ka=CA2mA∞m(A∞m−Am)
Thus, the ionization constant Ka of the weak acid (HA) in terms of molar conductivities is:
Ka=CA2mA∞m(A∞m−Am)
Topper's Solved these Questions
- ELECTROCHEMISTYBook:GRB PUBLICATIONChapter:ELECTROCHEMISTYExercise:Reasoning type
Explore 28 Videos
- ELECTROCHEMISTYBook:GRB PUBLICATIONChapter:ELECTROCHEMISTYExercise:Multiple objective type
Explore 33 Videos
- ELECTROCHEMISTYBook:GRB PUBLICATIONChapter:ELECTROCHEMISTYExercise:Faraday s Laws and Electrolysis
Explore 87 Videos
- D-BLOCK ELEMENTSBook:GRB PUBLICATIONChapter:D-BLOCK ELEMENTSExercise:Subjective Type
Explore 18 Videos
- ENVIRONMENTAL CHEMISTRY Book:GRB PUBLICATIONChapter:ENVIRONMENTAL CHEMISTRY Exercise:Straight objective type
Explore 40 Videos
Similar Questions
The dissociation constant of a weak acid HA is 4.9×10−8. Calculate for a decimolar solution of acid:.
% of ionisation
View SolutionIf Ka1andKa2 are the dissociation constants of two acids HA1andHA2, then the ratio of strengths of their solutions with equimolar concentration is ............. .
View Solution
Knowledge Check
The ionisation constant (Ka) of 0.1M weak monobasic acid (HA) will be whose degree of ionisation is 50% ?
A25×10−3B25×10−4C5×10−2D5×10−5The dissociation constant of two weak acids are ka1&ka2 respectively. Their relative strength is -
A(Ka2Ka1B(Ka1Ka2)12C(Ka1Ka2D(Ka1×Ka2Ka1)12A∞AgCl can be obtained:
Aby extrapolation of the graph A and √C to zero concentration.Bby known values of A∞ of AgNO3,HCl and HNO3Cboth a and bDNone of these
"At 250C the ionisation constant of weak mono acidic base is 10−9 .At the same temperature the pH of 0.1M solution of the base is
View SolutionIf x,y,z are in A.P and A1 is the A.M of x and y and A2 is the A.M of y and z then A.M of A1 and A2 is
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
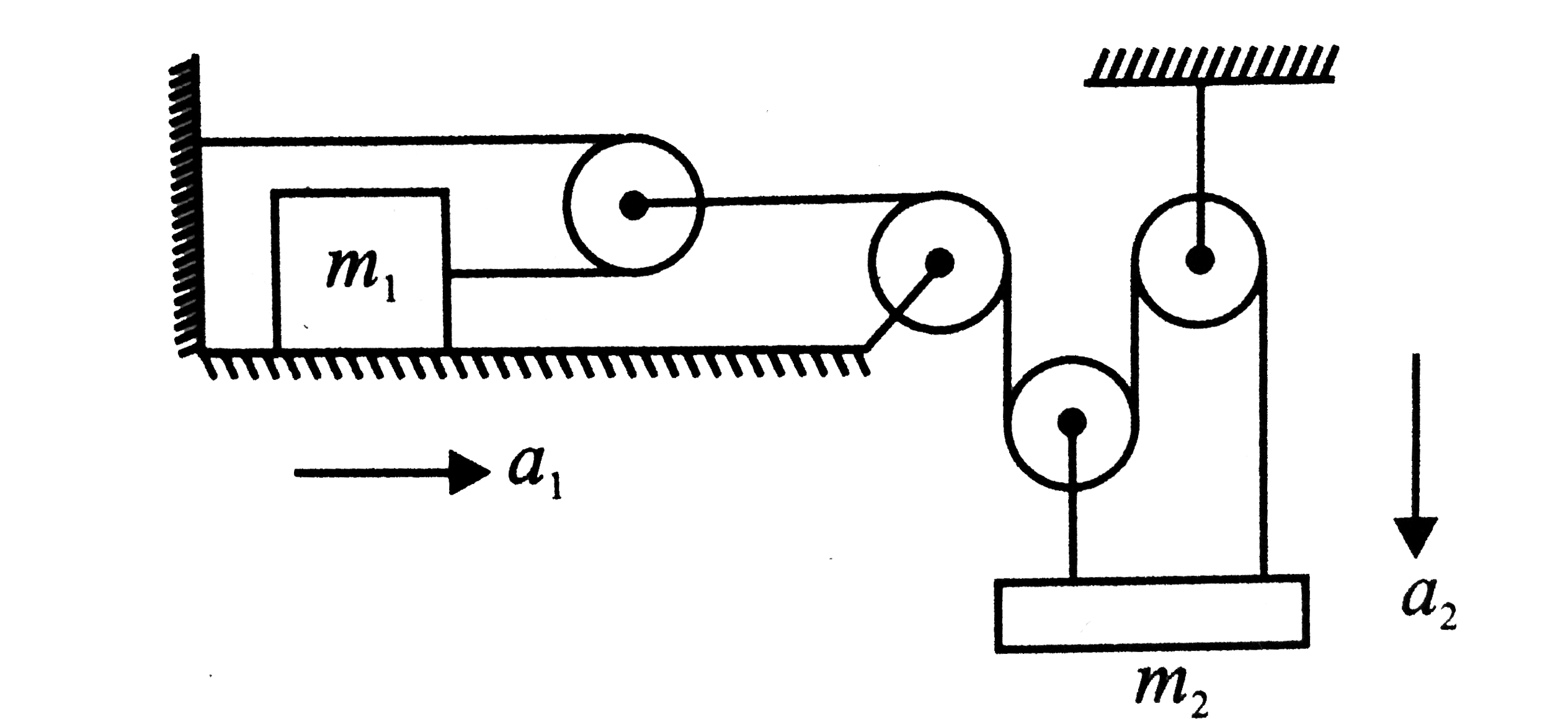
View Solution0.2M solution of a weak acid HA is 1% ionised 25∘C. Ka for the acid is equal to
View SolutionA weak acid HA and a weak base BOH are having same value of dissociation constants . If pH of 0.01MHA is 4, then pH of 0.01MBOH will be
View Solution