Sounds from two identical sources S1 and S2 reach a point P. When the sounds reach directly, and in the same phase, the intensity at P is I0. The power of S1 is now reduced by 64% and the phase difference between S1 and S2 is varied continuously. The maximum and minimum intensities recorded at P are now Imax and Imin
Imax=0.64I0
Imin=0.36I0
Imax/Imin=16
Imax/Imin=1.64/0.36
The correct Answer is:A, C
To solve the problem step by step, we will analyze the situation involving two identical sound sources S1 and S2 and how their intensities change when the power of one source is reduced and the phase difference is varied.
Step 1: Determine the Initial Intensity
Initially, when both sources S1 and S2 are in phase, the intensity at point P is given as I0. Since both sources are identical, we can express this as:
I0=I1+I2+2√I1I2
Given I1=I2=I, we have:
I0=2I+2√I2=2I+2I=4I
Thus, the initial intensity I can be expressed as:
I=I04
Step 2: Calculate the New Intensity of S1
The power of S1 is reduced by 64%. Therefore, the new intensity I′1 can be calculated as:
I′1=I1×(1−0.64)=I×0.36=0.36I
Step 3: Calculate Maximum Intensity Imax
The maximum intensity when the phase difference is varied is given by:
Imax=I′1+I2+2√I′1I2
Substituting I′1=0.36I and I2=I:
Imax=0.36I+I+2√0.36I⋅I
Calculating this gives:
Imax=0.36I+I+2⋅0.6I=1.36I+1.2I=2.56I
Step 4: Calculate Minimum Intensity Imin
The minimum intensity is given by:
Imin=I′1+I2−2√I′1I2
Substituting the values:
Imin=0.36I+I−2√0.36I⋅I
Calculating this gives:
Imin=0.36I+I−1.2I=1.36I−1.2I=0.16I
Step 5: Find the Ratio ImaxImin
Now, we can find the ratio of maximum to minimum intensity:
ImaxImin=2.56I0.16I=2.560.16=16
Step 6: Compare Imax and Imin with I0
- Since I0=4I:
- For Imax:
Imax=2.56I=0.64I0
- For Imin:
Imin=0.16I=0.04I0
Conclusion
The results are:
- Imax=0.64I0
- Imin=0.04I0
- The ratio ImaxImin=16
Initially, when both sources S1 and S2 are in phase, the intensity at point P is given as I0. Since both sources are identical, we can express this as:
I0=I1+I2+2√I1I2
Given I1=I2=I, we have:
I0=2I+2√I2=2I+2I=4I
Thus, the initial intensity I can be expressed as:
I=I04
The power of S1 is reduced by 64%. Therefore, the new intensity I′1 can be calculated as:
I′1=I1×(1−0.64)=I×0.36=0.36I
The maximum intensity when the phase difference is varied is given by:
Imax=I′1+I2+2√I′1I2
Substituting I′1=0.36I and I2=I:
Imax=0.36I+I+2√0.36I⋅I
Calculating this gives:
Imax=0.36I+I+2⋅0.6I=1.36I+1.2I=2.56I
The minimum intensity is given by:
Imin=I′1+I2−2√I′1I2
Substituting the values:
Imin=0.36I+I−2√0.36I⋅I
Calculating this gives:
Imin=0.36I+I−1.2I=1.36I−1.2I=0.16I
Now, we can find the ratio of maximum to minimum intensity:
ImaxImin=2.56I0.16I=2.560.16=16
- Since I0=4I:
- For Imax:
Imax=2.56I=0.64I0
- For Imin:
Imin=0.16I=0.04I0
The results are:
- Imax=0.64I0
- Imin=0.04I0
- The ratio ImaxImin=16
Topper's Solved these Questions
Similar Questions
Two identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
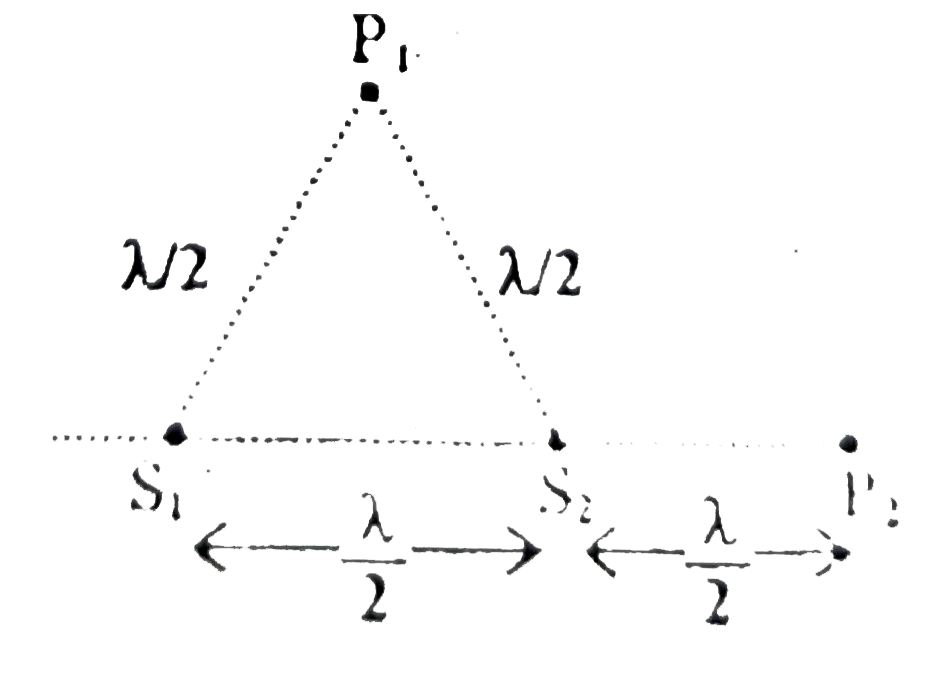
View Solution
Knowledge Check
Two identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
A2B4C5D6Two identical sound S1 and S2 reach at a point P is phase. The resultant loudness at point P is n dB higher than the loudness of S1 the value of n is :
A2B4C5D6A coherent light is incident on two paralle slits S1andS2. At a point P1 the frings will be dark if the phase difference between the rays coming from S1andS2 is
Anπ radiansB(n+0.5)π radiansC(2n+0.5)π radiansD(2n+1)π radians
S1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
View SolutionRatio waves originating from sources S1 and S2 having zero phase difference and common wavelength λ will show completely destructive interference at a point P is S1P−S2P is
View Solution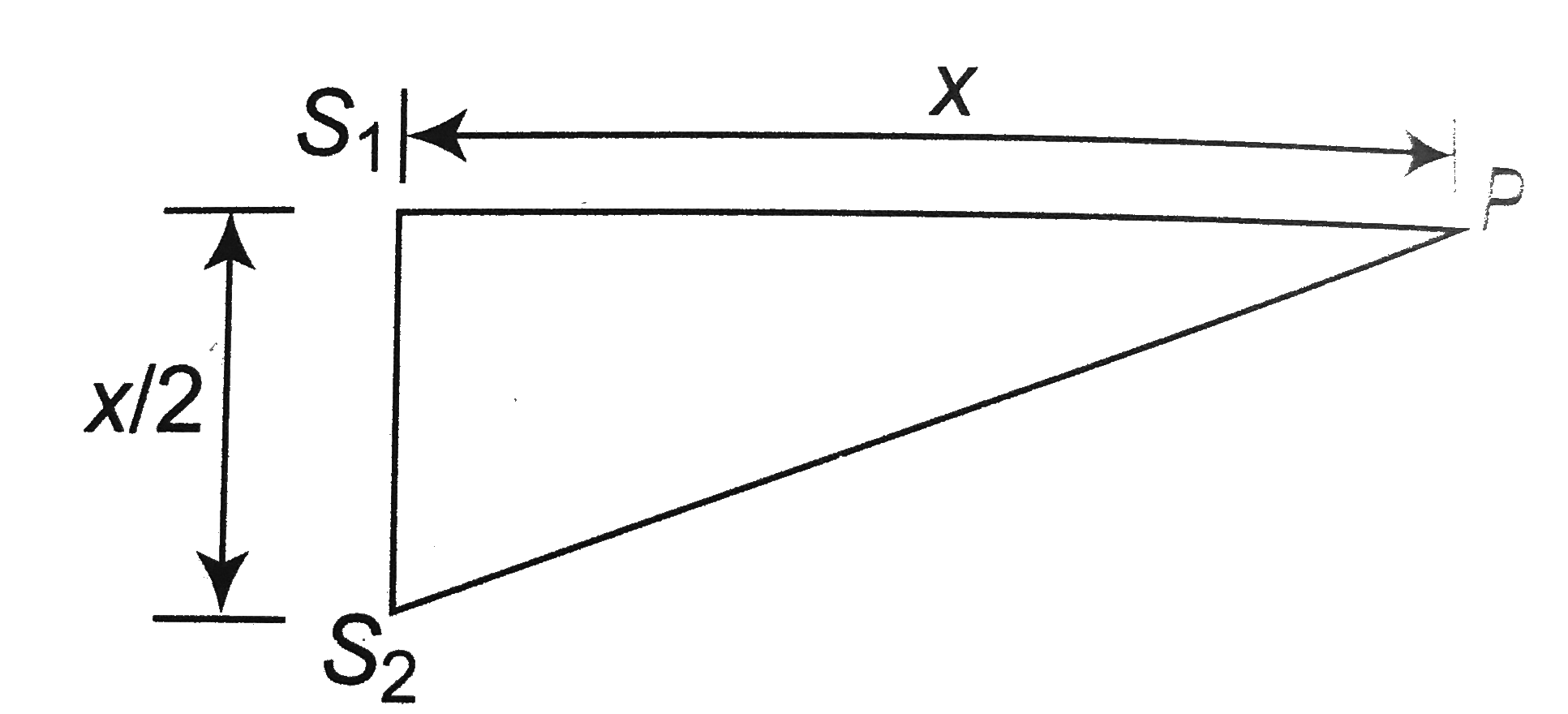
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View SolutionS1 and S2 are two sources of sound emitting sine waves. The two sources are in phase. The sound emitted by the two sources interfers at point F. The waves of wavelength :

View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
View Solution
