Two blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will

remain undisturbed
move up through a distance m2g/k and come to rest
undergo vertical SHM with a period of 2π√m1/k
undergo vertical SHM with time period of
2π√(m1+m2)/k
The correct Answer is:c
Step by step video, text & image solution for Two blocks of masses m_1 and m_2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m_2) drops off. The other block (m_1) will by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two blocks of masses m1=2kg and m2=4kg are attached to two ends of a light ideal spring of force constant k = 1000 N/m. The system is kept on a smooth inclined plane inclined at 30∘ with horizontal. The block m2 is attached to a light string whose other end is connected to a mass m3=1kg. A force F = 15N is applied on m1 and the system is released from rest. Assume initially the spring is at relaxed position and the system is released from rest. Find the
(a) maximum extension of the spring.
(

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View Solution
Knowledge Check
A ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
Ax=mgkBx=2mgkCthe ball will have no acceleration at the position where it has descended through x2Dthe ball will have an upward acceleration equal to g at its lowermost position.Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mgA block of mass M is attached to the lower end of a vertical rope of mass m. An upward force P acts on the upper end of the rope. The system is free to move. The force exerted by the rope on the block is PMM+m
Ain all casesBonly if the rope is uniformCin gravity-free space onlyDonly if P>(Mm)g
A mass of 0.2kg is attached to the lower end of a massless spring of force-constant 200N/m, the upper end of which is fixed to a rigid support. Which of the following statements is/are true?
View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
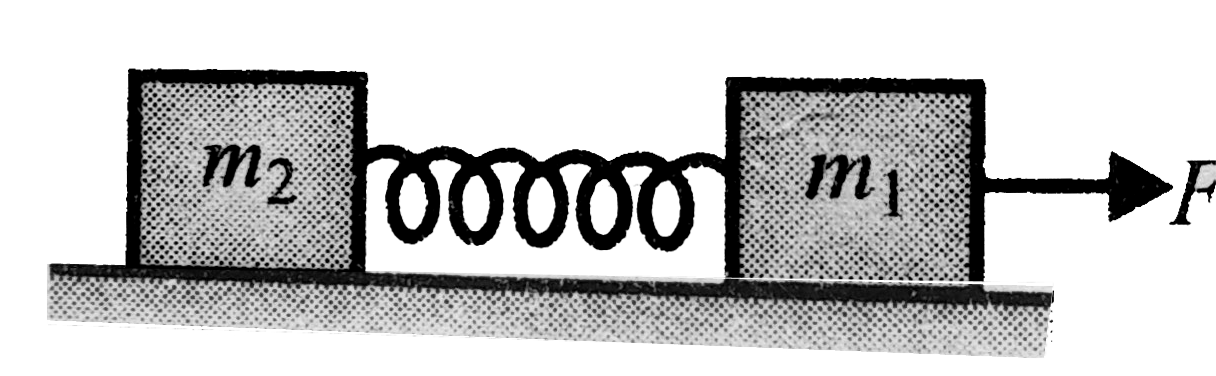
What is maximum elongation of spring.
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
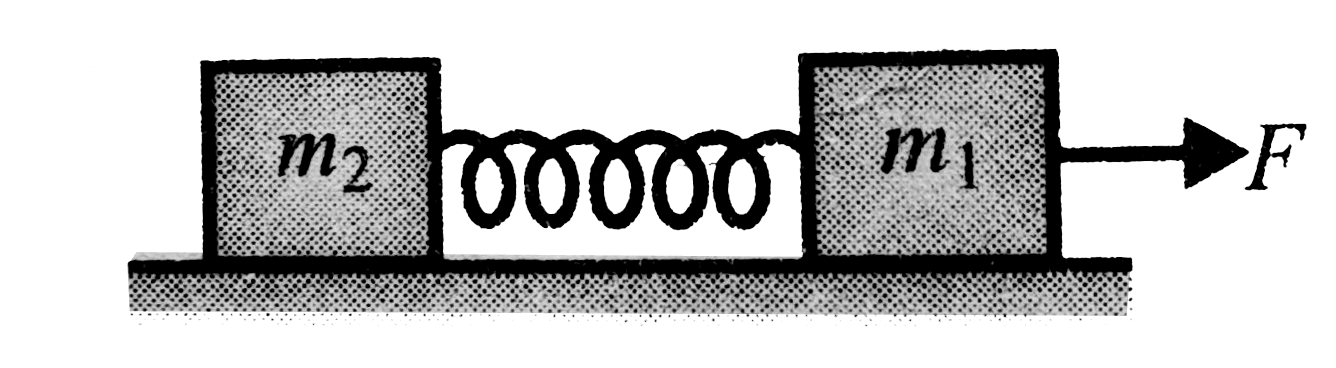
Which of the following statement is not true tn the watt of above system.
View Solution
