A car of mass m1 rests on a plank P of mass m2. The plank rests on a smooth floor. The string and pulley are ideal. The car starts and moves towards the pulley with acceleration.
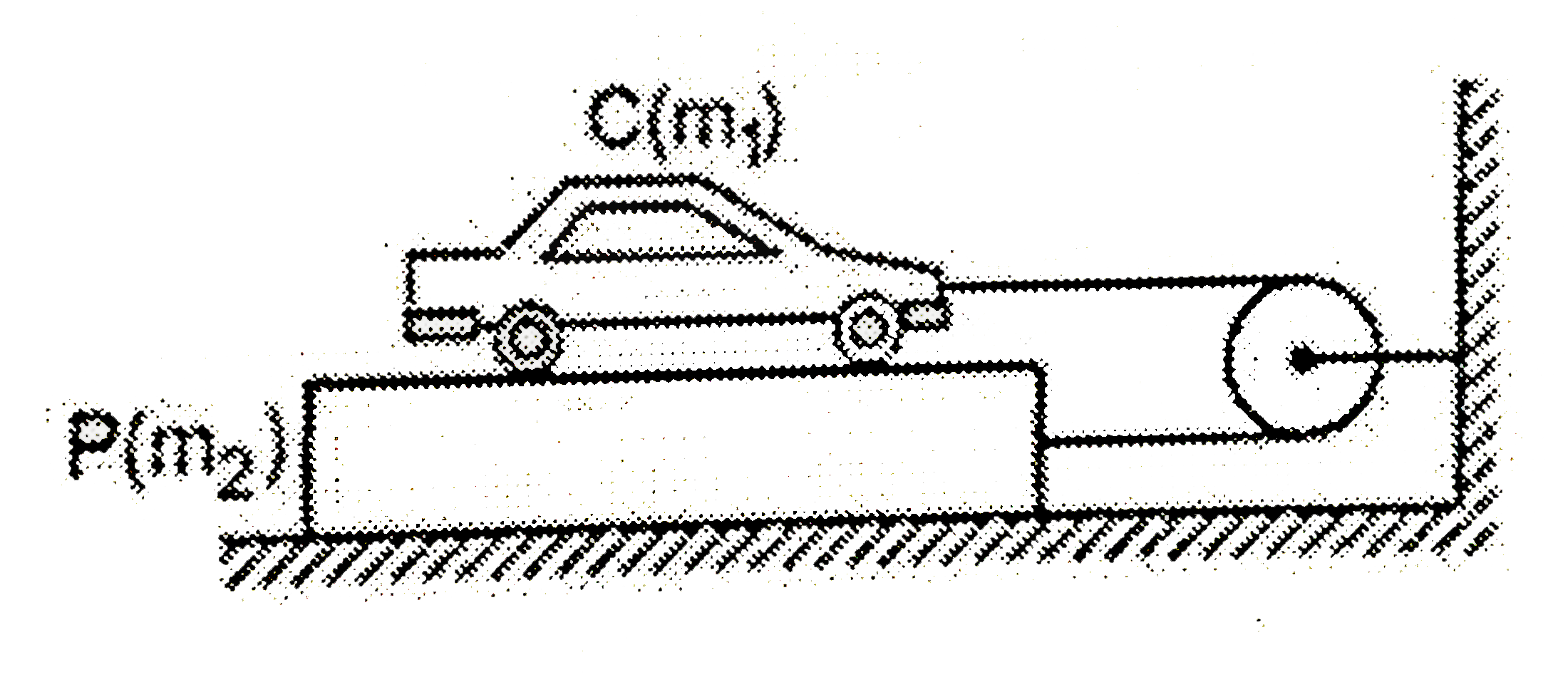
If m1>m2, the string will remain under tension.
If m1<m2, the string will become slack.
If m1=m2, the string will have no tension, and C and P will have accelerations of equal magnitude.
C and P will have acceleration of equal magnitude if m1≥m2.
The correct Answer is:A, B, C, D
Step by step video, text & image solution for A car of mass m_(1) rests on a plank P of mass m_(2). The plank rests on a smooth floor. The string and pulley are ideal. The car starts and moves towards the pulley with acceleration. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Type 2
22 Videos
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Revision Exercise
26 Videos
- IIT QUESTIONS 5BOOK - D MUKHERJEECHAPTER - IIT QUESTIONS 5EXERCISE - Matrix matching type
2 Videos
- MISCELLANEOUS QUESTION 1BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 1EXERCISE - Miscellaneous Questions-1 (Straight-Objective Type)
54 Videos
Similar Questions
A plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View SolutionFind the acceleration of masses m1 and m2 moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
View Solution
Knowledge Check
A car C of mass m1, rests on a plank of mass m2. The plank rests on a smooth floor. The string and pulley are ideal. If the car starts and moves towards the pulley with certain acceleration, choose the incorrect option:
 AIf m1>m2, the string will remain under tensionBIf m1<m2, the string will become slackCIf m1=m2, the string will have no tension, and C and P will have accelerations of equal magnitudesDC and P will have acceleration of unequal magnitude if m1≥m2
AIf m1>m2, the string will remain under tensionBIf m1<m2, the string will become slackCIf m1=m2, the string will have no tension, and C and P will have accelerations of equal magnitudesDC and P will have acceleration of unequal magnitude if m1≥m2A man of mass 80kg stands on a plank of mass 40kg. The plank is lying on a smooth horizontal floor. Initianlly both are at rest. The man starts walking on the plank towards north and stops after moving a distance of 6m on the plank. Then
AThe centre of mass of plank-man system remains stationaryBThe plank will slide to the north by a dsitance 4mCThe plank will slide to the south by a distance 4mDThe plank will slide to the south by a distance 12mIf the string & all the pulleys are ideal, acceleration of mass m is :-
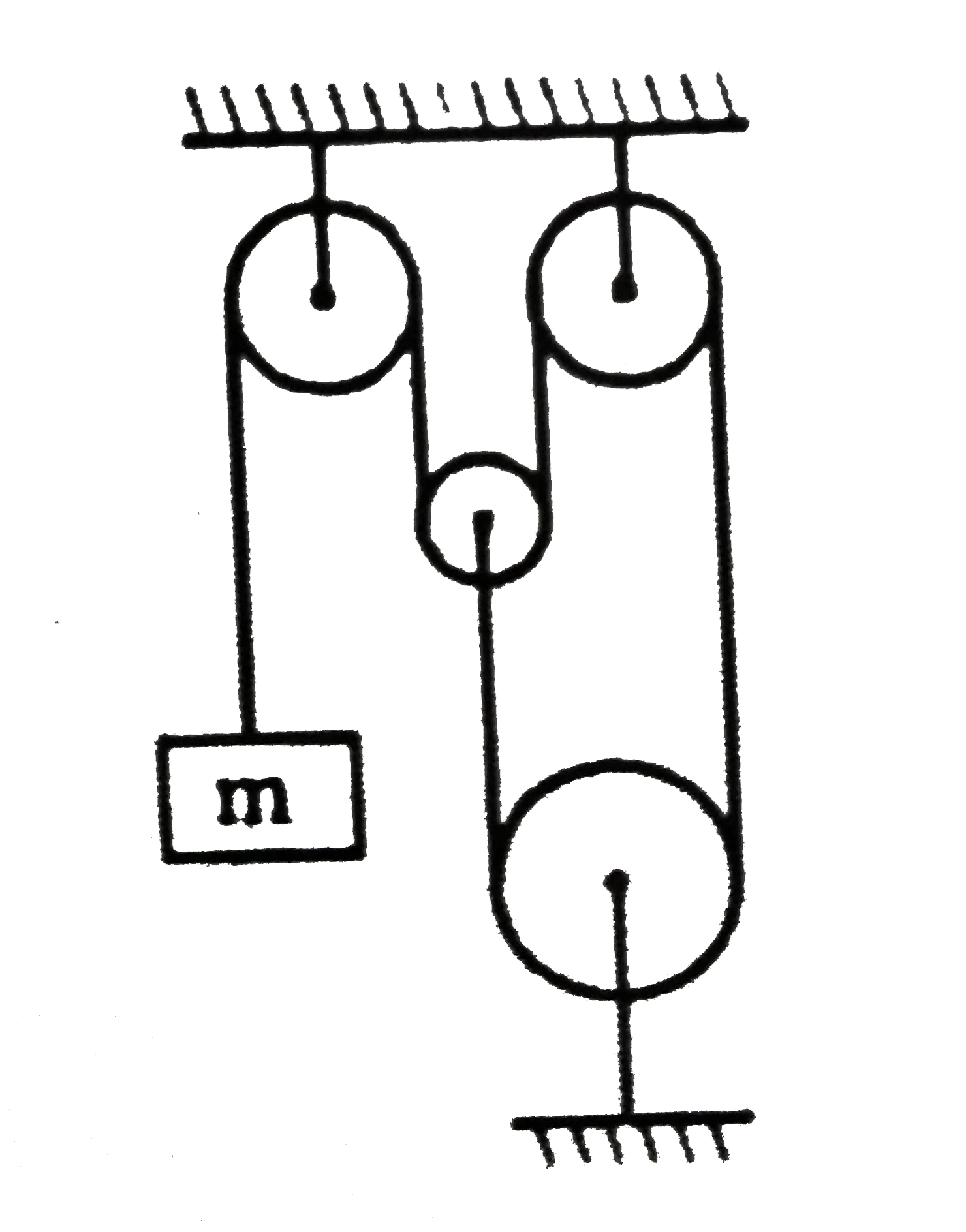 Ag2B0CgDdependent on m
Ag2B0CgDdependent on m
A man of mass m is moving with a constant acceleration a w.r.t plank is .The plank less on a smooth horizontal floor If the mass of plank m then calculate the acceleration of plank and man w.r.t ground and frictional force extended by plank on man

View SolutionA solid cylinder of mass m and radius R rest on a plank of mass 2m lying on a smooth horizontal surface. String connecting cylinder to the plank is passing over a massless pulley mounted on a movable light block B and the friction between the cylinder and the plank is sufficient to prevent slipping. if the block B is pulled with a constant forceF, the acceleration of the plank is 2Fxm then calculate x.

View SolutionA man of mass m1 stands at an edge A of a plank of mass m2 & length l which is kept on a smooth floor If man walks from A to the other edge B find displacement of plank.
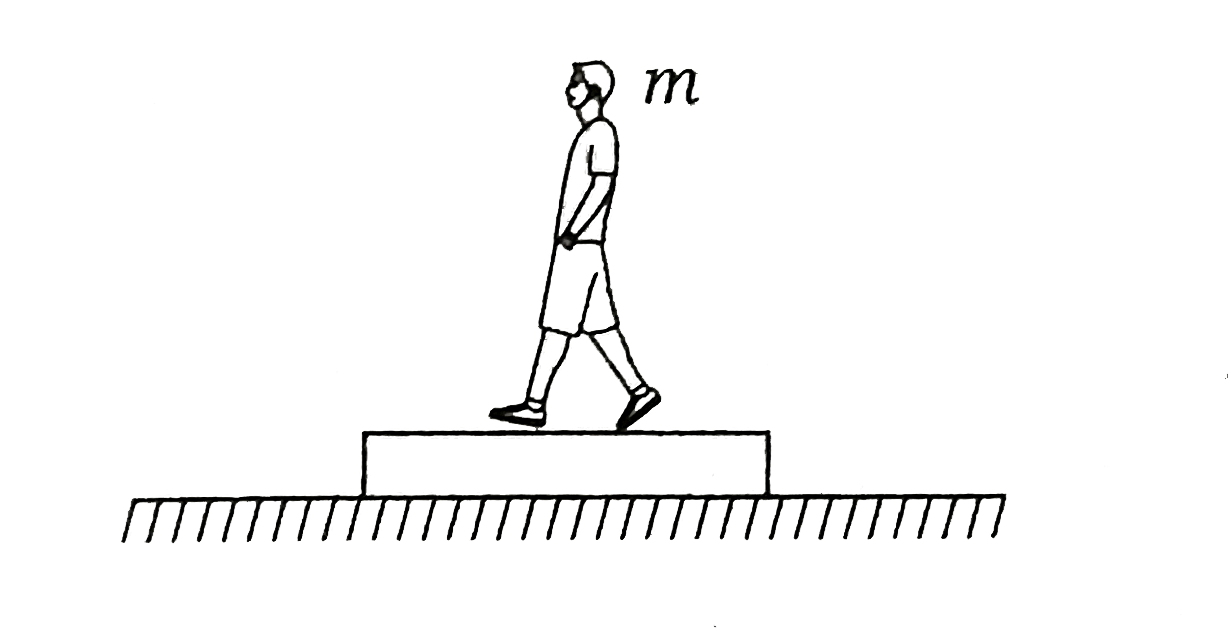
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :

View Solution
