A ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
Step by step video & image solution for A ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle alpha with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ball starts falling with zero initial velocity on a smooth inclined plane forming an angle α with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?
View SolutionA ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View Solution
Knowledge Check
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
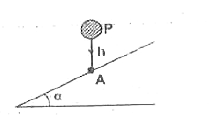 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the inclineA ball is projected with velocity u at right angle to the slope which inclined at an angle α with the horizontal. The distance x along the inclined plane that it will travell before again striking the slope is-
A2u2gcosαB2u2gtanαC2u2gtanαcosαD2u2gtanαsinαA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
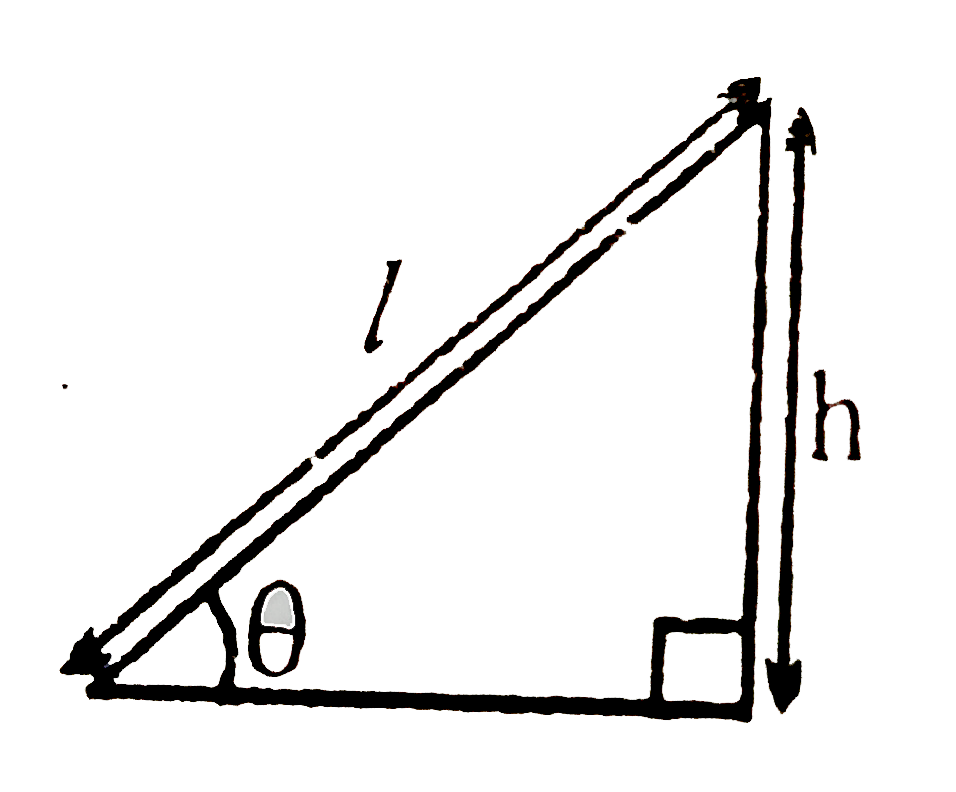 A√2hgB√2lgC√2lgsinθD1sinθ√h2g
A√2hgB√2lgC√2lgsinθD1sinθ√h2g
A body with zero initial velocity slips from the top of an inclined plane forming an angle α with the horizontal. The coefficient of friction μ between the body and the plane increases with the distance s from the top according to the law μ=bs. After what distance the body will stop.
View Solution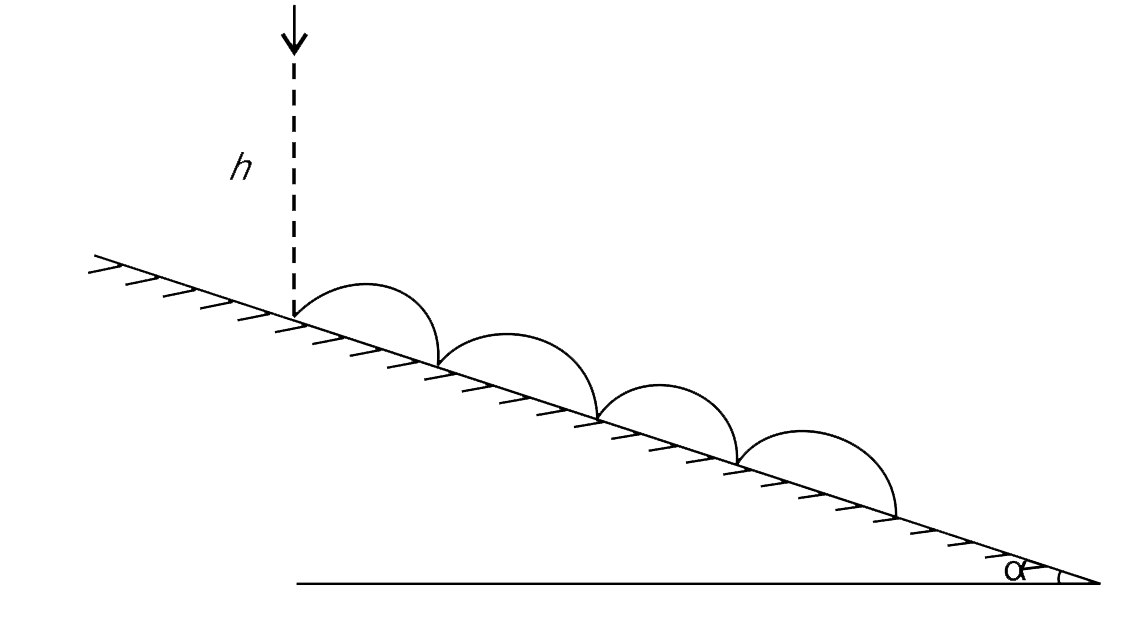
A ball is released in air above an incline plane inclined at an angle α to the horizontal. After falling vertically through a distance h it hits the incline and rebounds. The ball flies in air and then again makes an impact with the incline. This way the ball rebounds multiple times. Assume that collisions are elastic, i.e., the ball rebound without any loss in speed and in accordance to the law of reflection.
(a) Distance between the points on the incline where the ball makes first and second impact is l1 and distance between points where the ball makes second and third impact is l2. Which is large l1 or l2?
(b) Calculate the distance between the points on the incline where the ball makes second and fifth impact.
View SolutionA ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA disc of mass m slides with the zero initial velocity down an inclined plane of inclination θ to the harizontal, having traveled the distance d along the horizontal plane, the disc stops. Find the work performed by the friction over the whole distance, assuming the friction coefficient μ for both the inclined and horizontal planes.
View SolutionA small metal ball falls vertically and strickes a smooth plane inclined at an angle θ to the horizontal (θ<45∘). The ball rebounds horizontally. Show that a fraction (l-e) of the kinetic energy is lost during the impact and that if m is the mass and μ the speed of the ball before impact, the impulse on the plane is μsecθ. Here e isi the coefficient of restitutuon.
View Solution

