If A = { (x,y) : y = sin x, x ∈ R } and B = { (x,y) : y = cos x, x ∈ R} then A ∩ B contains Solution in Tamil
no element
infinitely many elements
only one element
cannot be determined.
The correct Answer is:A
Step by step video, text & image solution for If A = { (x,y) : y = sin x, x in R } and B = { (x,y) : y = cos x, x in R} then A cap B contains by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETS RELATIONS AND FUNCTIONSBook:SURA PUBLICATIONChapter:SETS RELATIONS AND FUNCTIONSExercise:ADDITIONAL PROBLEMS (SECTION - A)
Explore 20 Videos
- SETS RELATIONS AND FUNCTIONSBook:SURA PUBLICATIONChapter:SETS RELATIONS AND FUNCTIONSExercise:ADDITIONAL PROBLEMS (SECTION - B)
Explore 8 Videos
- SETS RELATIONS AND FUNCTIONSBook:SURA PUBLICATIONChapter:SETS RELATIONS AND FUNCTIONSExercise:EXERCISE 1.4
Explore 23 Videos
- QUESTION PAPER -19Book:SURA PUBLICATIONChapter:QUESTION PAPER -19Exercise:SECTION - IV
Explore 11 Videos
- SURAS MODAL QUESTION PAPER-1 MATHEMATICS Book:SURA PUBLICATIONChapter:SURAS MODAL QUESTION PAPER-1 MATHEMATICS Exercise:Section-IV
Explore 20 Videos
Similar Questions
Let f : R → R be defined as f(x) = x4. Choose the correct answer.
View SolutionIf n (A∩B) = 3 and n (A∪B) = 10 then find n [ P (AΔB)]
View SolutionFor the curve y = x3 given in figure draw,
y = -x3
View SolutionFor the given base curve y=sinx draw y=12sin2x
View SolutionThe formula for converting from Fahrenheit to Celsius temperatures is y = 5x9−1609. Find the inverse of this function and determine whether the inverse is also a function.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
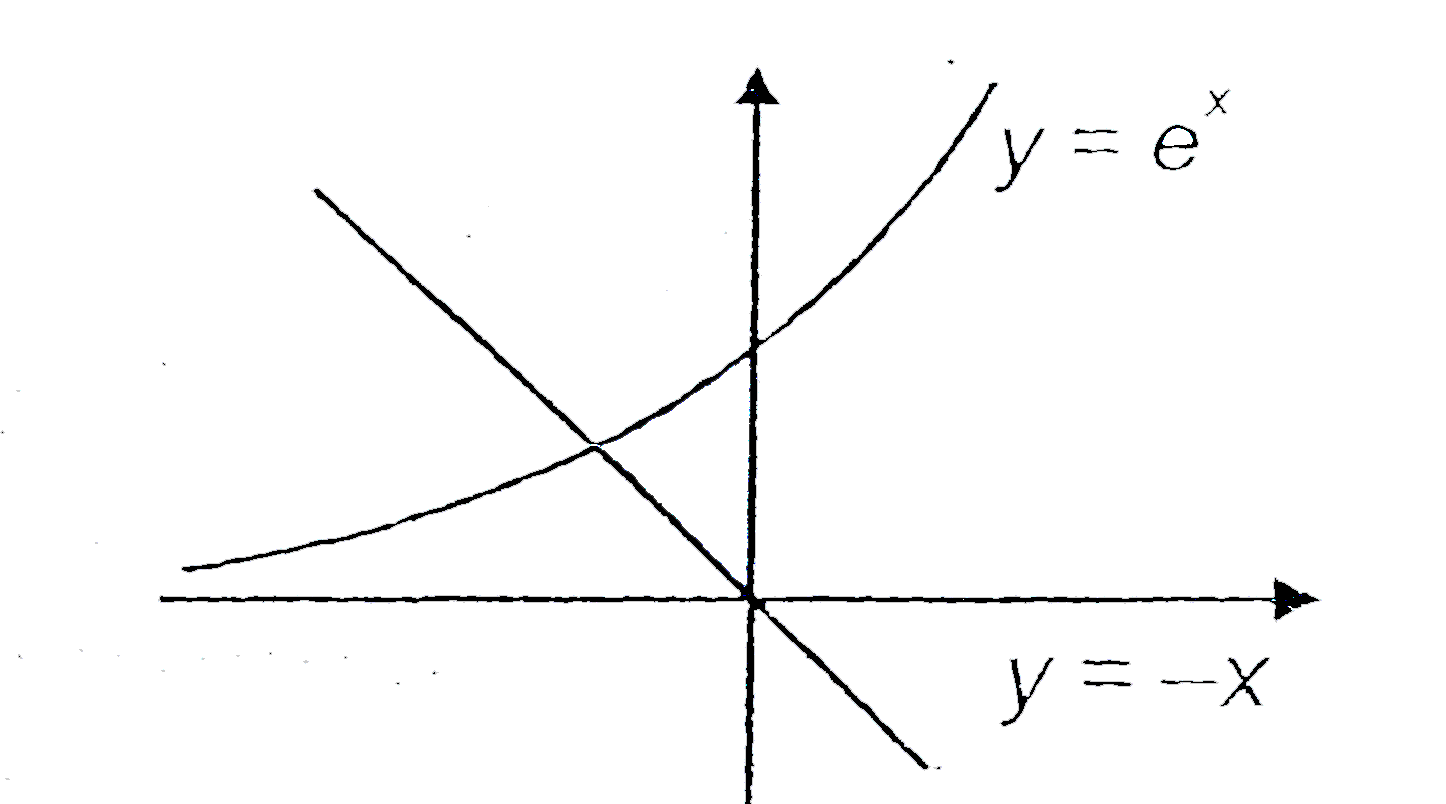
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
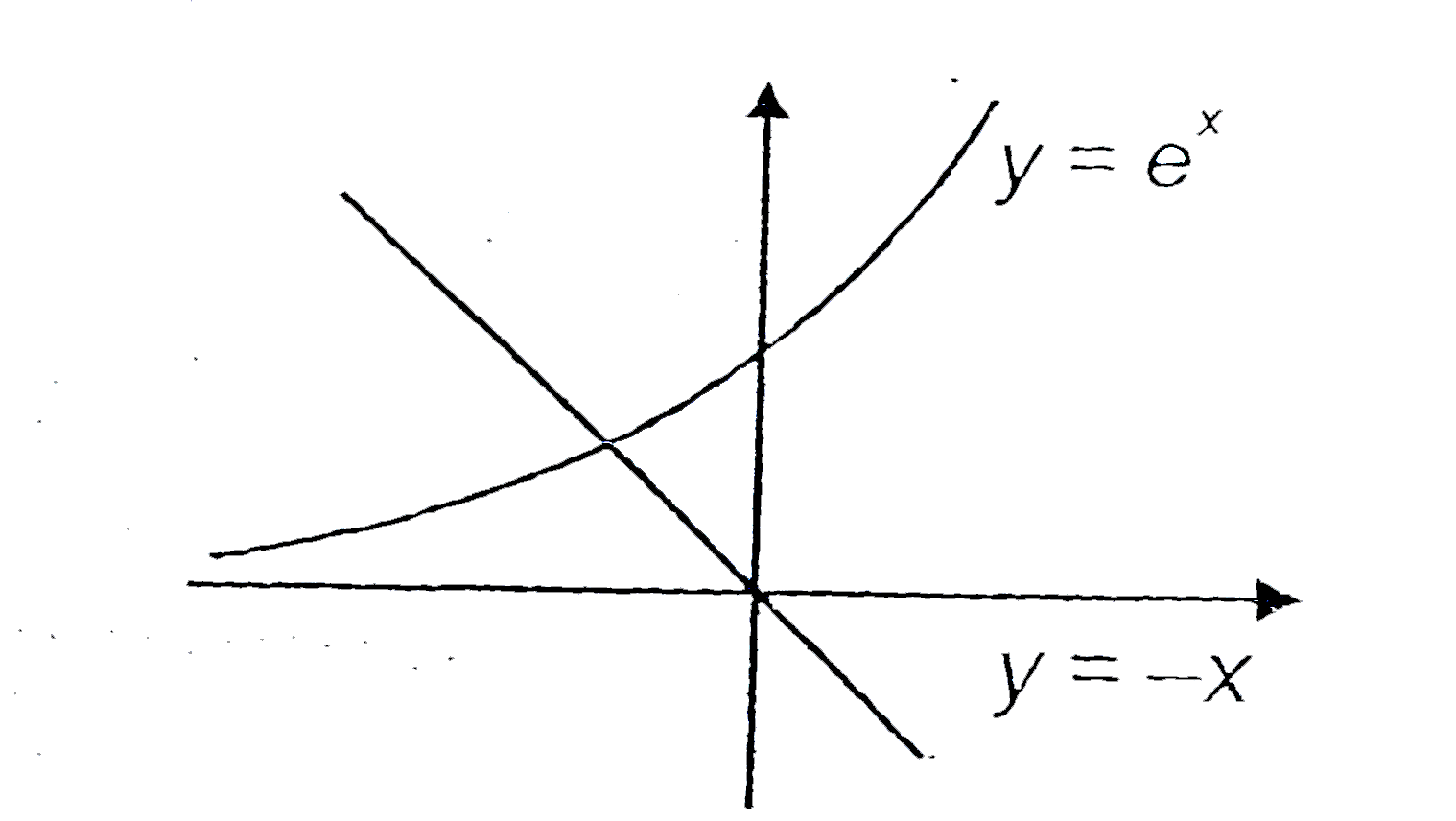
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
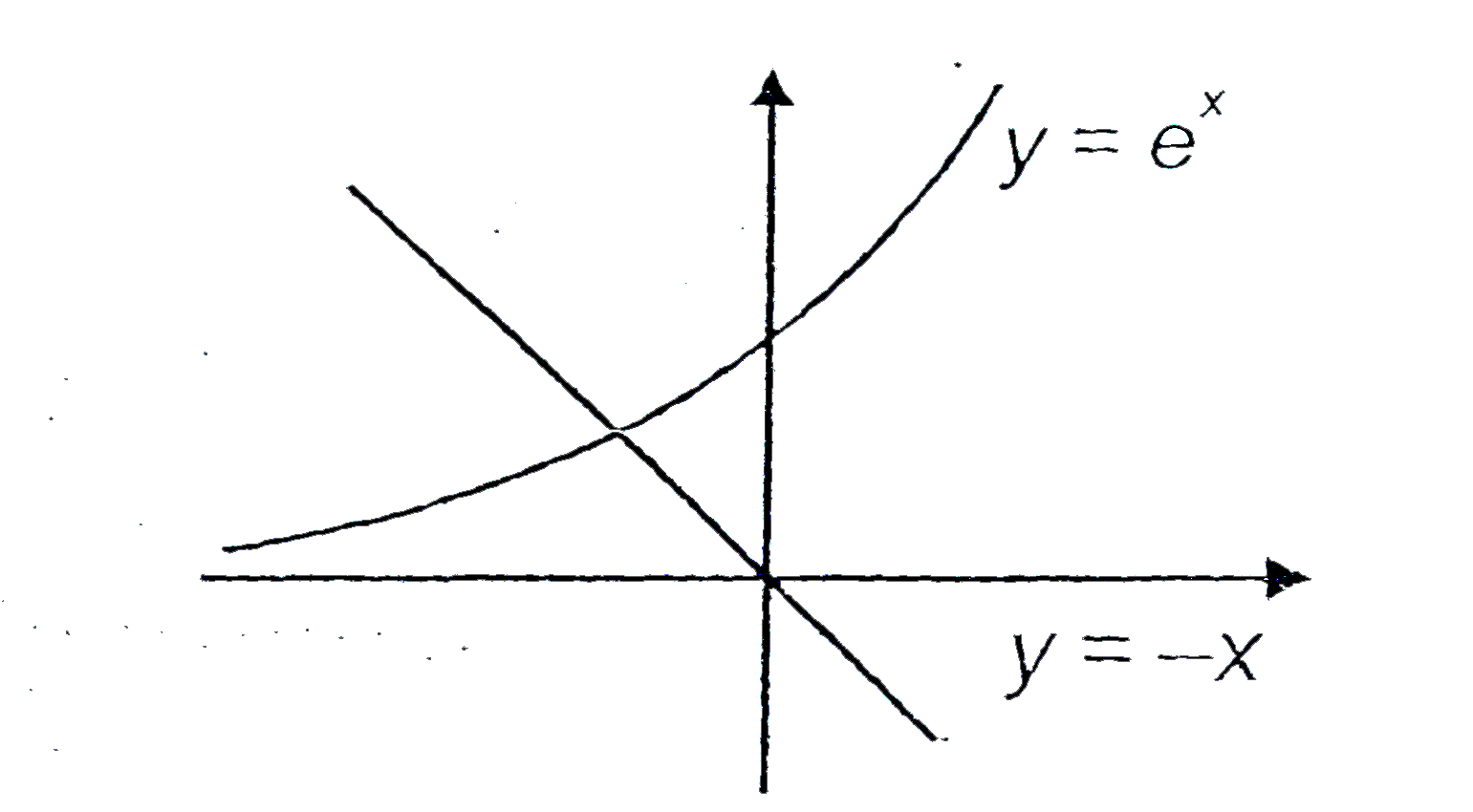
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
View SolutionIf A= {(x,y) : y = ex,x∈R} and B = { (x,y) : y = e−x,x∈R } then n (A ∩ B ) is
View SolutionA={(x,y):y=1/x,0≠x∈R},B={(x,y):y=−x,x∈R} then
View SolutionA={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R} then
View SolutionLet A={(x,y): y=ex,x∈R } , B={(x,y): y= e−x,x∈R } . Then :
View SolutionLet A={(x,y : y=ex,x∈R} , B={(x,y): y=x, x ∈ R} . Then :
View SolutionThe number of elements in the set A∩B∩C, where
A={(x,y)∈R×R,|x|+|y|≥1}
B={(x,y)∈R×R,x2+y2≥1}
and C={(x,y)∈R×R: max |x|,|y|=1} is:
View Solution

