A particle moves in the x-y plane under the action of a force →F such that the value of its linear momentum →P at any time t is Px=2 cost and py=2sint. What is the angle θ between →F and P at a given time t?
Step by step video & image solution for A particle moves in the x-y plane under the action of a force vecF such that the value of its linear momentum vecP at any time t is P_(x)=2 cost and p_(y)=2sint. What is the angle theta between vecF and P at a given time t? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-1
Explore 86 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-2
Explore 25 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
Similar Questions
A particle moves in the x-y plane under the action of a force →F such that the value of its linear momentum →P at any time t is Px=2 cost and py=2sint. What is the angle θ between →F and P at a given time t?
View SolutionA particle moves in the xy-plane under the action of a force F such that the components of its linear momentum p at any time t are px=2cost, py=2sint. The angle between F and p at time t is
View Solution
Knowledge Check
A particle moves in the x-y plane under the action of a force →F such that the value of its linear momentum →P at any time t is Px=2 cost and py=2sint. What is the angle θ between →F and P at a given time t?
Aθ=0∘Bθ=30∘Cθ=90∘Dθ=180∘A particle moves in the x-y plane under the action of a force →F such that the components of its linear momentum →P at any time t are px=costandpy=3sint. What is the magnitude of the vector →F?
A2√2B5C3D4F particle moves in x-y plane under the action of force →F such that the value of its linear momentum (→p) at any instant t is px=2 cos t and py=2 sin t. The angle θ between →F→P at a given time t will be-
A90∘B0∘C180∘D30∘
A particle moves in the xy plane under the influence of a force such that its linear momentum is →P(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants. The angle between the force and momentum is
View SolutionA particle moves in the X-Y plane under the influence of a force such that its linear momentum is →p(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants. The angle between the force and the momentum is
View SolutionA particle moves in the x-y plane under is influence of a force such that its linear momentum is →P(t)=A[ˆicos(kt)−ˆjsin(kt)], where A and k are constants Angle between the force and the momentum is:
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
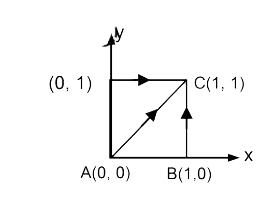
View SolutionThe momentum of a body is →P=2costˆi+2sintˆj. What is the angle between the force →F acting on the body and the momentum →P ?
View Solution

