सिद्ध कीजिए कि एक तनी हुई डोरी में सम तथा विषम दोनों प्रकार के संनादि उतपन्न किये जा सकते हैं।
Video Solution
Text Solution
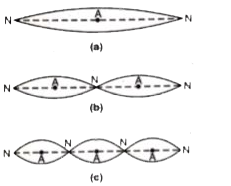
तनी हुई डोरी में प्रसामान्य विधाएँ-चूँकि अप्रगामी तरंग का विस्थापन समीकरण
Y=2asin(2πx)λcos(2πvt)λ ...(1)
चूँकि x= 0 तथा x =l पर (अर्थात् दृढ़ सिरों पर) विस्थापन शून्य होगा, अतः सीमा शर्ते निम्नलिखित हैं :
x = 0 पर Y = 0 तथा x = l पर Y = 0 ...(2)
अत: समीकरण (1) से स्पष्ट है कि x = 0 पर Y = 0
परन्तु x = l पर Y = 0 होने के लिए 0=2asin(2πl)λcos(2πvt)λ
अर्थात् t के सभी मानों के लिए
sin(2πl)λ=0
2πlλ=0,π,2π,...=nπ
जहाँ n एक पूर्णांक है, अर्थात् n = 0, 1, 2, 3,....
∴λ=2lnn ...(3)
कम्पन की प्रथम विधा-यदि n = 1, तो
λ1=2l तथा आवृत्ति n1=Vλ1=V2l
यदि डोरी में तनाव T तथा डोरी की एकांक लम्बाई का द्रव्यमान m है, तो अनुप्रस्थ तरंग की चाल
v=√Tm
∴ आवृत्ति n1=12l√Tm ...(4) इसे मूल स्वर या प्रथम संनादी स्वर कहते हैं। यह विधा चित्र में प्रदर्शित है।
कम्पन की द्वितीय विधा-यदि n= 2, तो λ2=2l2 तथा आवृत्ति n2=Vλ2=2V2l
∴n2=22l√Tm=2n1 ...(5)
इसे द्वितीय संनादी या प्रथम अधिस्वरक कहते हैं। यह विधा चित्र b में प्रदर्शित है।
कम्पन की तृतीय विधा-यदि n =3, तो λ3=2l3∴n3=Vλ3=3V2l
n3=32l√Tm=3n1 ....(6)
इसे तृतीय संनादी या द्वितीय अधिस्वरक कहते हैं। यह विधा चित्र c में प्रदर्शित है।
इस प्रकार, n1:n2:n3:......=1:2:3...
स्पष्टतः तनी हुई डोरी में सम तथा विषम दोनों प्रकार के संनादी उत्पन्न किया जा सकते हैं।"
|
Similar Questions
सममित तथा विषम सममित आव्यूह | किसी वर्ग आव्यूह का एक सममित तथा एक विषम सममित आव्यूह के योगफल के रूप में निरूपण | उदाहरण
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionसीखें सम और विषम फलन एक क्लास में
View Solutionअथवा 'कारतूस' पाठ के आधार पर सोदाहरण सिद्ध कीजिए कि वज़ीर अली एक जांबाज़ सिपाही था।
View Solutionतनी डोरी में अनुप्रस्थ तरंग की चाल
View Solutionतनी हुई डोरी मे अप्रगामी तरंगे तथा कंपन की विधाये एवं कंपन के नियम
View Solutionऊँट तथा कैक्टस निम्नलिखित में किस प्रकार के वासस्थान के लिए अनुकूलित हैं?
View Solutionफलनों के प्रकार: प्रश्नोत्तर #!#आवर्ती फलन #!#सम/विषम फलन
View Solution
