ऊष्मा चालकता गुणांक का सूत्र प्राप्त कर इसकी परिभाषा, मात्रक व विमीय सूत्र लिखिए।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

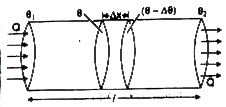
ocr_image
स्थायी अवस्था में किसी एक समान अनुप्रस्थ परिच्छेद क्षेत्रफल वाली एक सुचालक छड़ के समतापी पृष्ठों के अभिलम्बवत् t समय में प्रवाहित होने वाली ऊष्मा की मात्रा-
(1) पृष्ठ के क्षेत्रफल के अनुक्रमानुपाती होती है।
(2) पृष्ठों के बीच ताप-प्रवणता के अनुक्रमानुपाती होती है।
(3) समय t के अनुक्रमानुपाती होती है।
(4) छड़ की लम्बाई के अनुक्रमानुपाती होती है।
माना एक l लम्बाई की छड़ का अनुप्रस्थ परिच्छेद क्षेत्रफल.A है। स्थायी अवस्था में दो समतापी समतल पृष्ठों के ताप क्रमशः θ व (θ−Δθ), इनके बीच लम्बवत् दूरी Δx तथा छड़ के सिरों का ताप θ1 व θ2 है। तब t सेकण्ड में छड़ से प्रवाहित ऊष्मा की मात्रा
∝−AΔθΔxt[∵ ताप प्रवणता या =−ΔθΔx]Q
Q=−KAΔθΔxt
Q=KA(θ1−θ2)tl [∵−ΔθΔx=(θ1−θ2)l]
जहाँ K एक नियतांक है जिसे छड़ के पदार्थ का ऊष्मा चालकता गुणांक कहते हैं। तब उपर्युक्त समीकरण से-
K=Q×lA×(θ1−θ2)×t यही अभीष्ट सूत्र है।
परिभाषा-यदि l= 1 m , A =1m2,(θ1−θ2)=1∘C और t = 1 सेकण्ड हो, तो
K=Q
अर्थात् “किसी पदार्थ का ऊष्मा चालकता गुणांक ऊष्मा की वह मात्रा है जो स्थायी अवस्था में उस पदार्थ की 1 मीटर लम्बी व 1m2 अनुप्रस्थ क्षेत्रफल की छड़ जिसके दोनों सिरों का तापान्तर 1∘C हो, से 1 सेकण्ड में प्रवाहित होती है, जबकि ऊष्मा का प्रवाह छड़ के सिरों के लम्बवत् हो।"
S.I. पद्धति में इसका मात्रक जूल मीटर −1∘C−1 सेकण्ड −1 है | इसका विमीय सूत्र [MLT−3θ−1] है।

Updated on:21/07/2023
|