Question

जड़त्व आघूर्ण की लम्बवत अक्ष की प्रमेय का कथन लिखिए एवं सिद्ध कीजिए।

Explanation

प्रमेय - किसी पिण्ड के तल में स्थित दो परस्पर लंबवत अक्षों के परितः पिण्ड के जड़त्व आघुर्णों का योग उस तीसरी अक्ष के परितः पिण्ड के जड़त्व आघूर्ण के बराबर होता है, जो दोनों अक्षों के लंबवत होती है तथा उनके कटान बिंदु में से होकर गुजरती है।

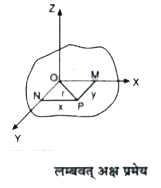
उपपत्ति - माना की चित्रानुसार पिण्ड के बिंदु P पर द्रव्यमान m का कोई कोण है जिसकी X , Y और Z अक्ष से दूरियाँ क्रमशः y , x और r है। अतः समकोण `DeltaPMO ` में `r^(2)=x^(2)+y^(2)` दोनों पक्षों में m का गुणा करने पर `mr^(2)=mx^(2)+my^(2)` तथा सम्पूर्ण पिण्ड के लिए `Sigma mr^(2)=Sigma mx^(2)=Sigma my^(2)`
यदि x , y और z अक्षों के परितः पिण्ड के जड़त्व आघूर्ण क्रमशः `I_(x), I_(y)` और `I_(z)` हों तब `Sigma mr^(2)=I_(z), Sigma mx^(2)=I_(y)` और `Sigma my^(2)=I_(x)` लिखने पर,
`I_(z) =I_(x)+I_(y)`, यही लंबवत अक्षों का प्रमेय है।