दो कार P व Q एक ही क्षण बिन्दु से एक सरल रेखा में चलना प्रारम्भ करती है तथा किसी क्षण t पर उनकी स्थितियाँ xp(t)=at+bt2xQ(t)=ft−t2 तथा है दोनों कोरों का वेग समान होने का समय होगा :
a+f2(1+b)
f−a2(1+b)
a−f1+b
a+f2(b−1)
The correct Answer is:B
vP=dxPdt=a+2bt तथा vQ=dxQdt=f−2t
vP=vQ जबकि a+2bt=f−2t या t=f−a2(b+1).
Topper's Solved these Questions
- सरल रेखा में गति Book:SHIVLAAL PUBLICATIONChapter:सरल रेखा में गति Exercise:बोधात्मक प्रश्न
Explore 8 Videos
- समतल में गति Book:SHIVLAAL PUBLICATIONChapter:समतल में गति Exercise:वस्तुनिष्ठ प्रश्न
Explore 58 Videos
- सरल रेखा में गति एवं समतल में गति Book:SHIVLAAL PUBLICATIONChapter:सरल रेखा में गति एवं समतल में गति Exercise:एक शब्द/ वाक्य में उत्तर
Explore 8 Videos
Similar Questions
क्या यह सम्भव है कि
किसी वस्तु का वेग नियत हो, लेकिन चाल परिवर्ती हो ?
View Solutionनिम्नलिखित में से अदिश राशि है :
View Solutionθ कोण पर झुके हुए दो सदिश →A व →B के परिणामी सदिश के परिणाम के लिए सूत्र लिखिए|
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionनिम्नलिखित कथनो में से सत्य असत्य लिखिए और अपने उत्तर का औचित्य भी दीजिए।
किसी रेखा से समान दूरी पर स्तिथ बिन्दुओ का समुच्चय एक रेखा होती है।
View Solutionदो कार P ओर Q एक ही क्षण पर के बिंदु से एक सरल रेखा में चलना प्रारंभ करती है। किसी क्षण t पर उनकी स्थितियाँ xp(t)=at+bt2 तथा xQ(t)=ft−t2 हैं। दोनों कारों के वेग समान होने का समय होगा -
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
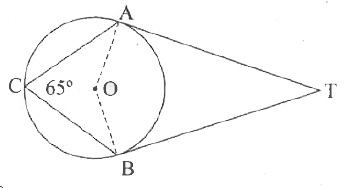
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionउस सरल रेखा का समीकरण जो बिन्दु (1,-2) से गुजरती है तथा रेखा 3x-5y+7=0 के लम्बवत है, है
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View Solution

