if 7−2k≤3, what si the least possible value of 2k+7?
−3
10
11
13
The correct Answer is:C
To solve the inequality 7−2k≤3 and find the least possible value of 2k+7, we can follow these steps:
Step 1: Solve the inequality
Start with the given inequality:
7−2k≤3
Step 2: Isolate the term involving k
Subtract 7 from both sides:
−2k≤3−7
This simplifies to:
−2k≤−4
Step 3: Divide by -2
When dividing by a negative number, remember to flip the inequality sign:
k≥2
Step 4: Find the expression 2k+7
We need to find the least value of 2k+7. Substitute k with the minimum value from the inequality:
2k+7=2(2)+7
Step 5: Calculate the value
Now calculate:
2(2)+7=4+7=11
Conclusion
Thus, the least possible value of 2k+7 is:
11
---
Start with the given inequality:
7−2k≤3
Subtract 7 from both sides:
−2k≤3−7
This simplifies to:
−2k≤−4
When dividing by a negative number, remember to flip the inequality sign:
k≥2
We need to find the least value of 2k+7. Substitute k with the minimum value from the inequality:
2k+7=2(2)+7
Now calculate:
2(2)+7=4+7=11
Thus, the least possible value of 2k+7 is:
11
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 4c+20≥31, what is the least possible value of 12c+7 ?
A18B40C51D58If −5c−7≤8, what is the least possible value of 15c+7 ?
A−38B−4C15D22If −6<−4r+10≤2, what is the least possible value of 4r+3?
A2B5C8D11
If 2x2+3ax−7<−17, what is the smallest possible integer value of a when x=−1?
View SolutionIF k3 is divisible by 240, what is the least possible value of integer k?
View SolutionIf |x|≤2and|y|≤1, then what is the least possible value of x-y?
View Solution25=(ky−1)2
In the equation above y=-2 is one solution. If K is a constant, what is a possible value of k?
View Solution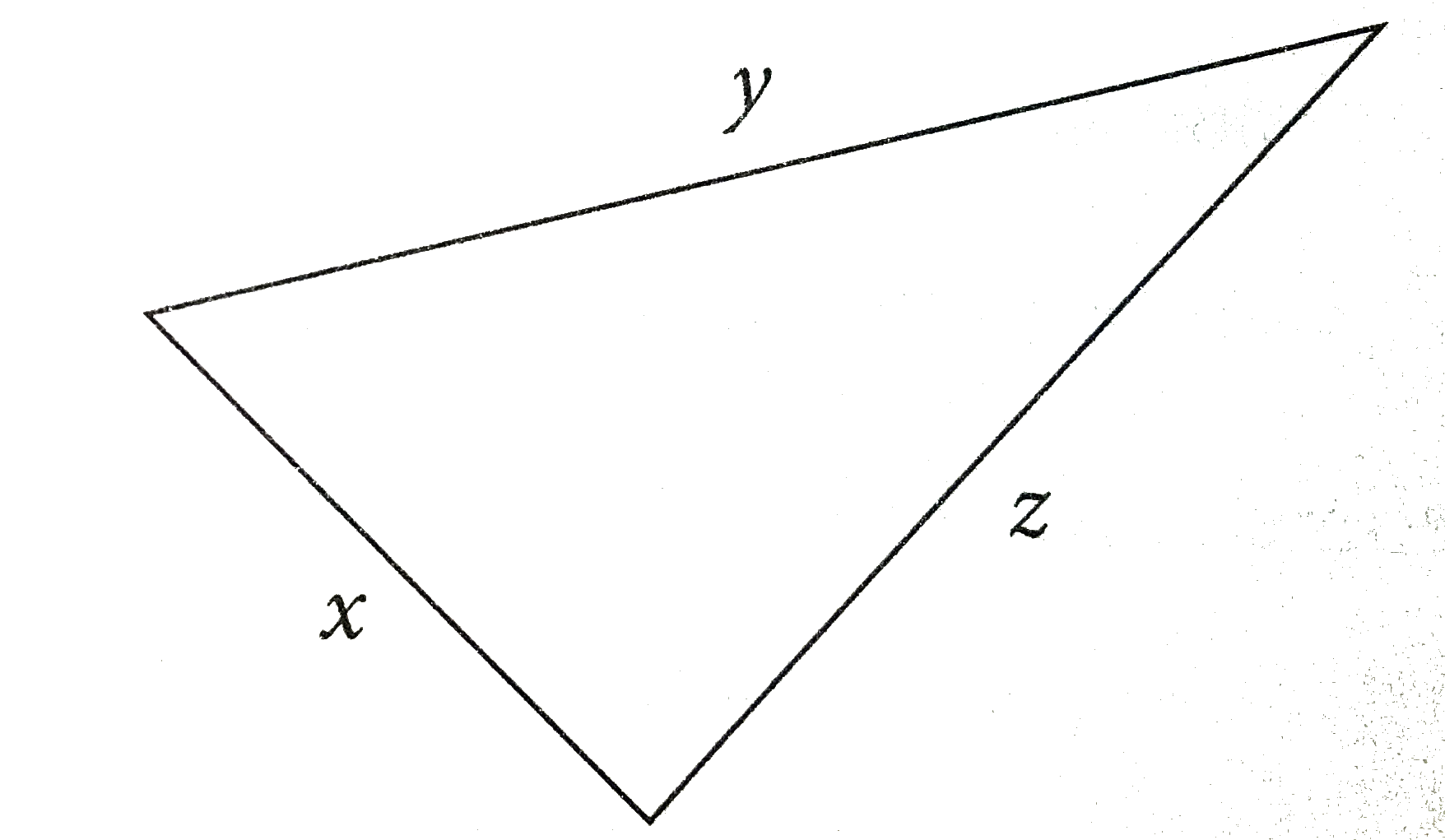
In the figure above, if x=7 and y=11, what is the difference between the greatest and least possible integers value of z?
View Solution
