For all real numbers x , f(2x) = x2−x+3. An expression for f(x) in terms of x is
2x2−2x+3
4x2−2x+3
x24−x2+3
x22−x2+3
The correct Answer is:C
f(x)=f(2⋅x2)=(x2)2−x2+3=x24−x2+3.
Topper's Solved these Questions
Similar Questions
If f(x) is a function f:R→R, we say f(x) has property I. If f(f(x))=x for all real numbers x. II. f(−f(x))=−x for all real numbers x. How many linear functions, have both property I and Il ?
View SolutionLet h(x)=f(x)−a(f(x))3 for every real number x
h(x) increase as f(x) increses for all real values of x if
View Solution
Knowledge Check
If the function f(x) is defined for all real numbers x as the maximum value of 2x+4and12+3x then for which one of the following values of x will f(x) actually values of x will f(x) actually equal 2x+4?
A−4B−5C−6D−9If f(x) = x2−4 , for what real number values of x will f(f(x))= 0 ?
A2.4B±2.4C2 or 6D±1.4or±2.4A function f(x) is defined for all real numbers by the expression (x−1.5)(x−2.5)(x−3.5)(x−4.5). For which one of the following values of x, represented on the number line is f(x) negative?
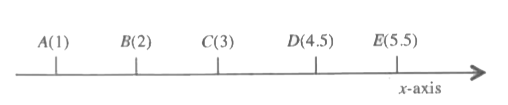
The graph is not drawn to scale.APoint ABPoint BCPoint CDPoint D
Let f(x) be a quadratic expression which is positive for all real x and g(x)=f(x)+f'(x)+f''(x).A quadratic expression f(x) has same sign as that coefficient of x2 for all realx if and only if the roots of the corresponding equation f(x)=0 are imaginary.Which of the following holds true? (A) g(0)g(1)<0 (B) g(0)g(−1)<0 (C) g(0)f(1)f(2)>0 (D) f(0)f(1)f(2)<0
View SolutionLet f(x)be real valued continous funcion on R defined as f(x) =x2e−|x|
Number of points of inflection for y=f(x) is (a) 1 (b) 2 (c) 3 (d) 4
View SolutionIf f : R→R,f(x)=x3 and g : R→R, g (x) =2x2+1, and R is the set of real number, then find fog (x) and gof (x).
View SolutionLet f:R→R be a differentiable function satisfying f(x+y)=f(x)+f(y)+x2y+xy2 for all real numbers x and y. If limx→0f(x)x=1, then
The value of f(9) is
View SolutionLet f be a function such that f(x+y)=f(x)+f(y) for all xandyandf(x)=(2x2+3x)g(x) for all x, where g(x) is continuous and g(0) = 3. Then find f'(x)
View Solution

