The intersection of a plane with a right circular cylinder could be which of the following ?
I. A circle
II . Parallel lines
III. Intersecting lines
I only
II only
III only
I and II only
The correct Answer is:D
To determine the possible intersections of a plane with a right circular cylinder, we will analyze each option provided in the question.
Step 1: Understanding the Geometry
A right circular cylinder has a circular base and extends vertically. When a plane intersects with this cylinder, the shape of the intersection depends on the orientation of the plane.
Hint: Visualize the cylinder and consider how a flat surface (the plane) can cut through it.
Step 2: Analyzing Option I - A Circle
If the plane is horizontal and cuts through the cylinder, the intersection will be a circle. This is because the cross-section of the cylinder at any height is a circle.
Hint: Think about how slicing a cylindrical object horizontally yields a circular shape.
Step 3: Analyzing Option II - Parallel Lines
If the plane cuts vertically and is parallel to the axis of the cylinder, the intersection will yield two parallel lines. This occurs because the plane intersects the curved surface of the cylinder at two points, creating two parallel lines.
Hint: Imagine a vertical slice through the cylinder that does not touch the top or bottom edges.
Step 4: Analyzing Option III - Intersecting Lines
For the intersection to yield intersecting lines, the plane would need to cut through the cylinder at an angle that creates two lines that cross each other. However, this is not possible with a right circular cylinder because the surface is curved. Therefore, intersecting lines cannot be formed.
Hint: Consider the nature of the cylinder's surface and how a plane interacts with it.
Conclusion
Based on the analysis:
- A circle (Option I) is possible.
- Parallel lines (Option II) are also possible.
- Intersecting lines (Option III) are not possible.
Thus, the correct answer is that the intersection can be a circle or parallel lines, which corresponds to option 4 (One and Two only).
Final Answer: Option 4 (One and Two only).
A right circular cylinder has a circular base and extends vertically. When a plane intersects with this cylinder, the shape of the intersection depends on the orientation of the plane.
If the plane is horizontal and cuts through the cylinder, the intersection will be a circle. This is because the cross-section of the cylinder at any height is a circle.
If the plane cuts vertically and is parallel to the axis of the cylinder, the intersection will yield two parallel lines. This occurs because the plane intersects the curved surface of the cylinder at two points, creating two parallel lines.
For the intersection to yield intersecting lines, the plane would need to cut through the cylinder at an angle that creates two lines that cross each other. However, this is not possible with a right circular cylinder because the surface is curved. Therefore, intersecting lines cannot be formed.
Based on the analysis:
- A circle (Option I) is possible.
- Parallel lines (Option II) are also possible.
- Intersecting lines (Option III) are not possible.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Line A passes through the cooredinate points (−25,0)and(0,1). Which of the following lines will line A never intersect ?
A B
B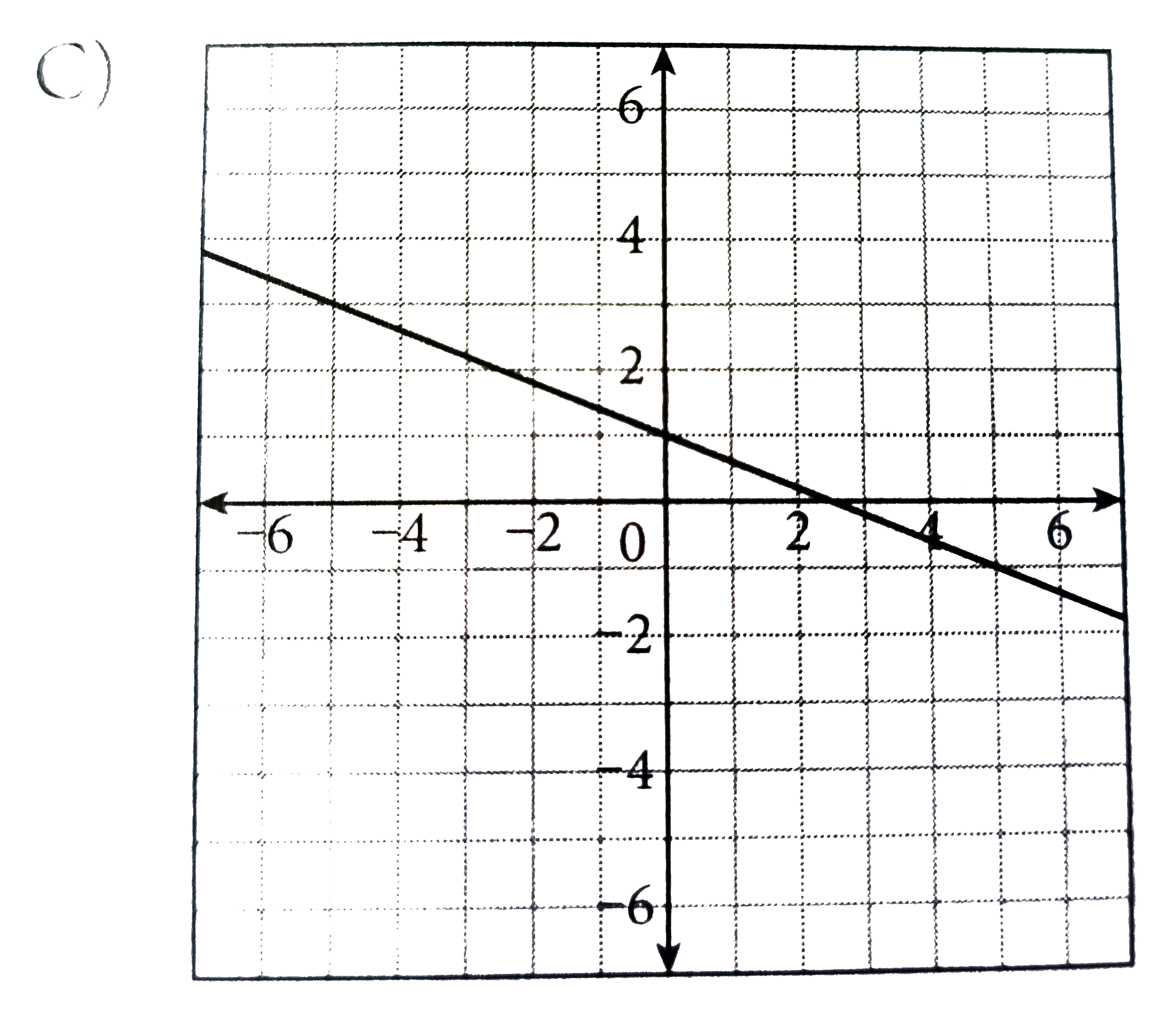 C
C D
D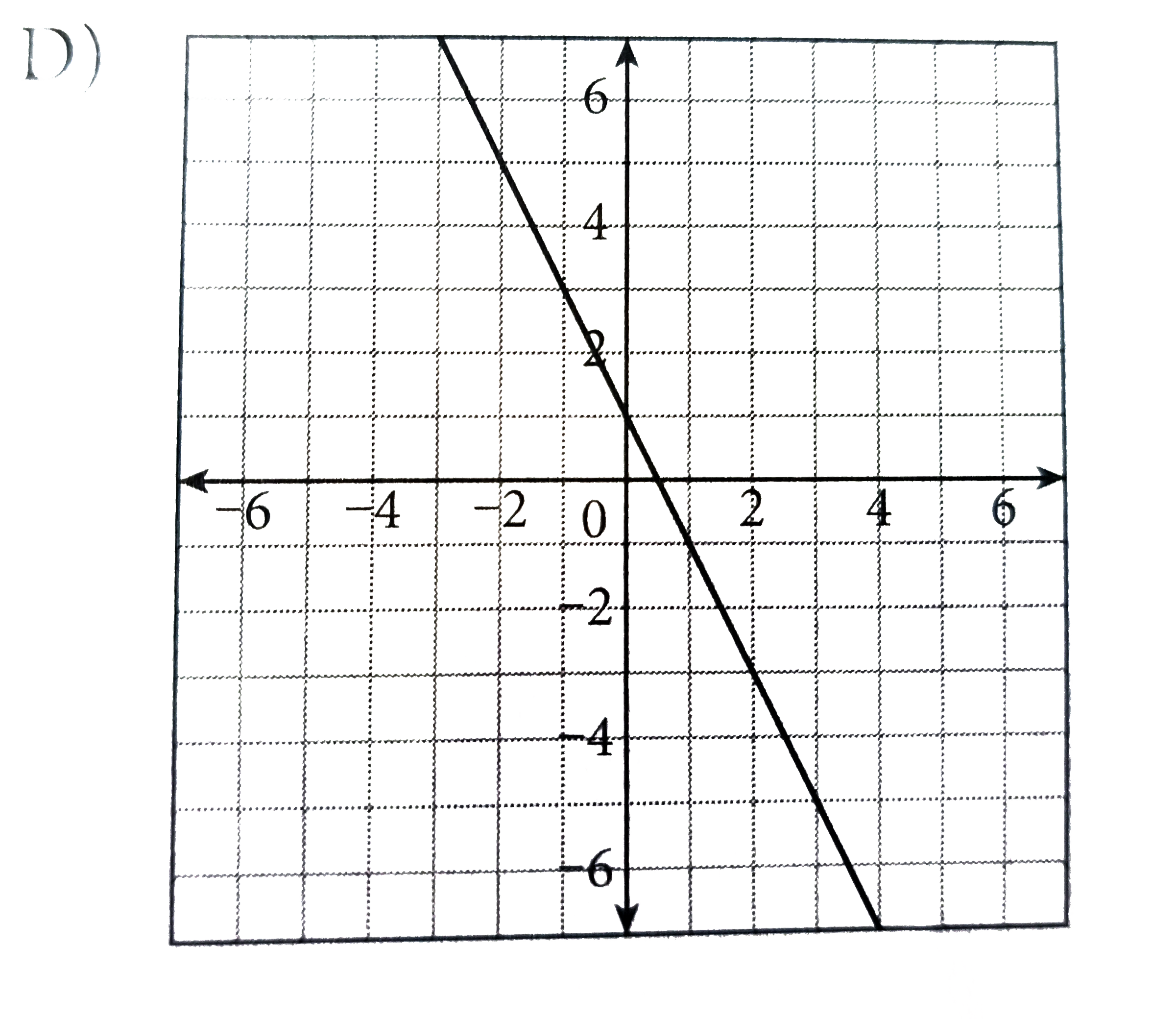
The converse of the statement If two lines are parallel , then they do not intersect in the plane is
A1. If two lines do not intersect in the same plane then they are parallel.B2. If two lines are not parallel then they do not intersect in the same plane.C3. If two lines are not parallel then they intersect in the same plane.D4. none of the above
State which of the following pairs of line segments or rays appear to be parallel :
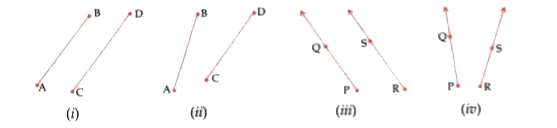
View SolutionFind, which of the following sets are empty :
The set of points of intersection of two parallel lines.
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is(A) a square (b) a circle (C) a straight line (d) two intersecting lines
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is
(a)a square (b) a circle (c) a straight line (d) two intersecting lines
View SolutionWrite the converse of the following satement: If the two lines are parallel, then they do not intersect in the same plane.
View SolutionState which of the following statements are true (T) or which are false (F) If two lines in the same plane do not intersect, then they must be parallel.
Distance between two parallel lines is not same everywhere.
If m⊥l, n ⊥ l and m ≠n, then mn
Two non-intersecting coplanar rays are parallel.
No two parallel segments intersect.
Every pair of lines is a pair of coplanar lines.
Two lines perpendicular to the same line are parallel.
A line perpendicular to one of two parallel lines is perpendicular to the other.
View Solution

