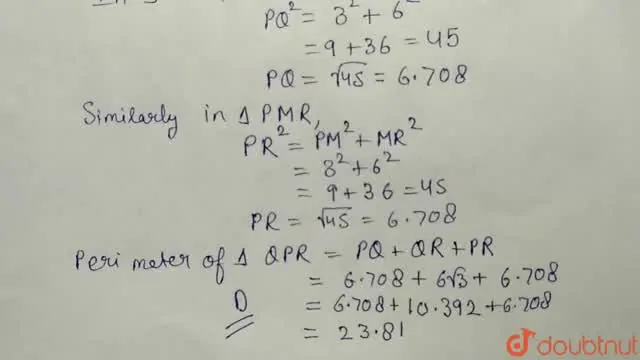The cube in the figure above has edges of length 6 If point p is the midpoint of an edge, what is the perimeter of △QPR?
13.41
14.28
17.1
23.81
The correct Answer is:D
By the pythagorean theorem, QP and RP each equal √62+32=√45. Apply the Pythagorean theorem to find SR2=62+62, and QR2=62+62+62, so QR=6√3. Therefore, the perimeter of △QPR=2√45+6√3=23.81 [15]
Related Playlists
Similar Questions

In figure above , what is the length of AB?View Solution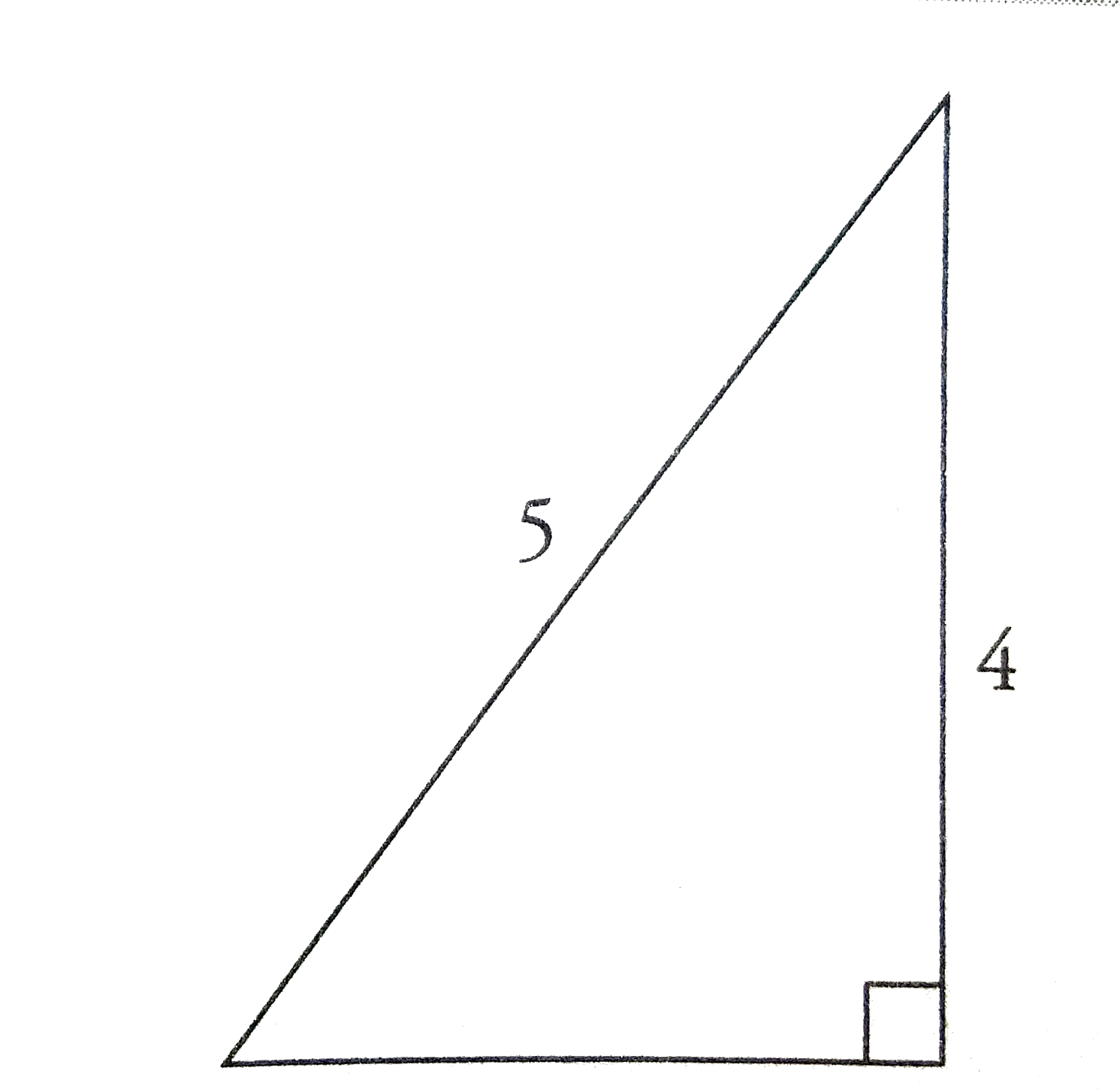
If the area of the triangle above is 6, what is its perimeter?View Solution
In the figure above, if the edge length of the cube is 4, what is the shortest distance from A to D?View SolutionThe cube in figure has edge length √2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00ˆi,(b)−2.00ˆj,and(c)−3.00ˆj+4.00ˆk . (d) what is the total flux through the cube for each field ?
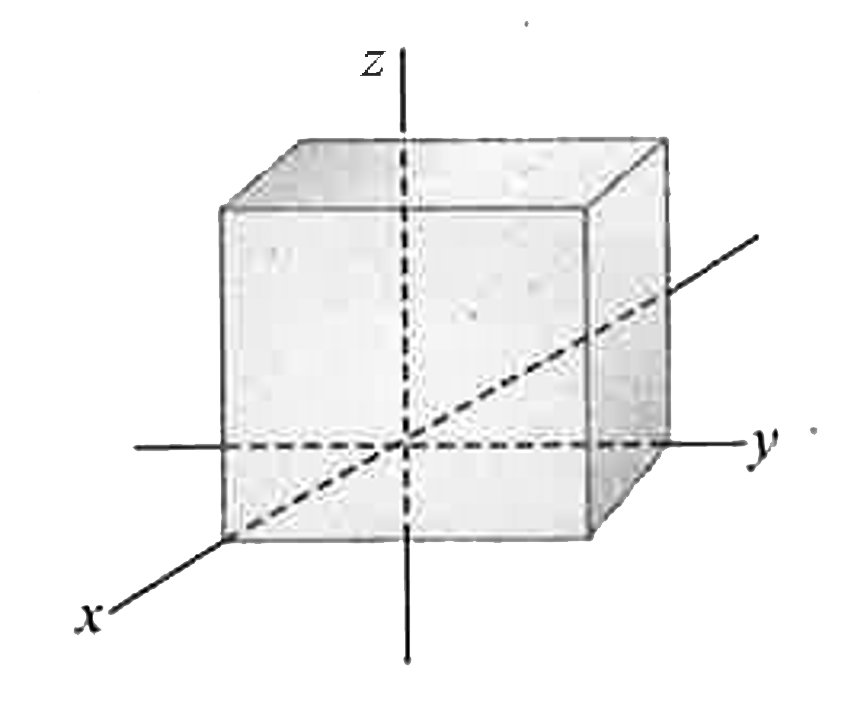 View Solution
View SolutionIf the length of an edge of cube A is one-third the length of an edge of cube B, what is the ratio of the volume of cube A to the volume of cube B?
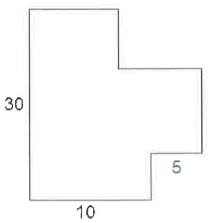
View SolutionIn the figure above, adjacent sides meet at right angles and the lengths given are in inches. What is perimeter of the figure, in inches?
 View Solution
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
 View Solution
View SolutionA solid cube has an edge length of 5. what is the ratio of the cube's surface area of its volume?
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe edge length of a cube is 400 pm .its body diagonal would be
View Solution