
In the figure above, the graph of y=f(x) has two transformations performed on it. First it is rotated 180∘ about the origin, and then it is reflected about the x-axis. Which of the following is the equations of the resulting curve?
A
y=-f(x)
B
y=f(x+2)
C
x=f(y)
D
y=f(x)
Video Solution
Text Solution
The correct Answer is:D
The two transformations put the graph right back where it started. [12]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The graph shows a parabola that is symmetric about the x-axis. Which one of the following could be the equation of the graph?
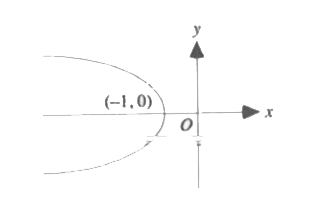 Ax=−y2−1Bx=−y2Cx=−y2+1Dx=y2−1
Ax=−y2−1Bx=−y2Cx=−y2+1Dx=y2−1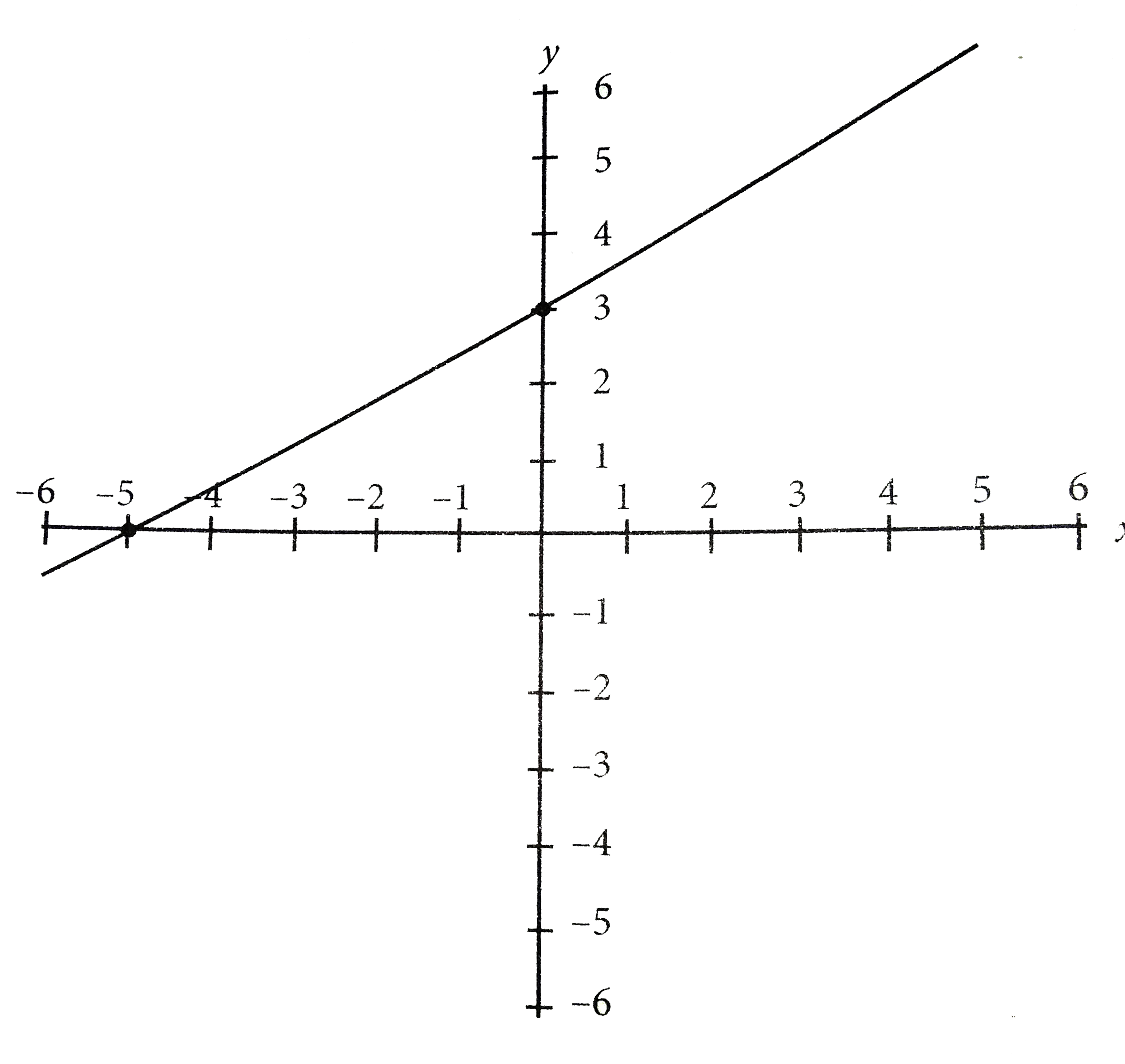
In the figure above, of y=f(x) is shown. Which of the following could be the equation of f(x)?Af(x)=−35x+3Bf(x)=−35x−3Cf(x)=35x−3Df(x)=35x+3The region in the first quadrant bounded by the line 3x+2y=7 and the coordinate axes is rotated about the x-axis .What is the volume of the resulting solid ?
A8 units3B20 units3C30 units3D40 units3
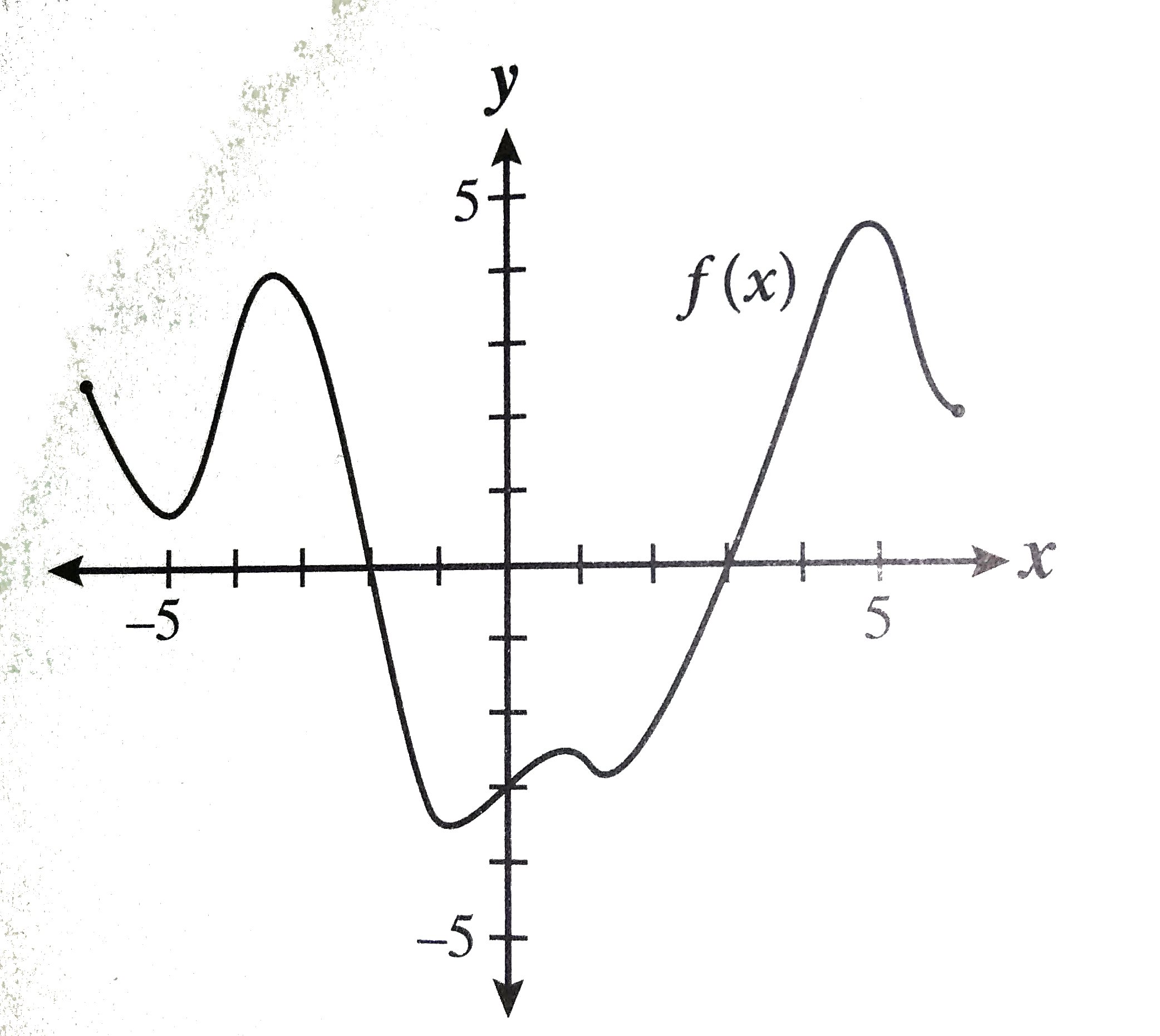
The figure above shows the graph of f(x). For which value(s) of x does f(x) equal 0?
View Solutionconsider the function f(X) =x+cosx
which of the following is not true about y =f(x)?
View SolutionGiven the graph of y=f(x), which of the following is graph of y=f(1−x)
View Solution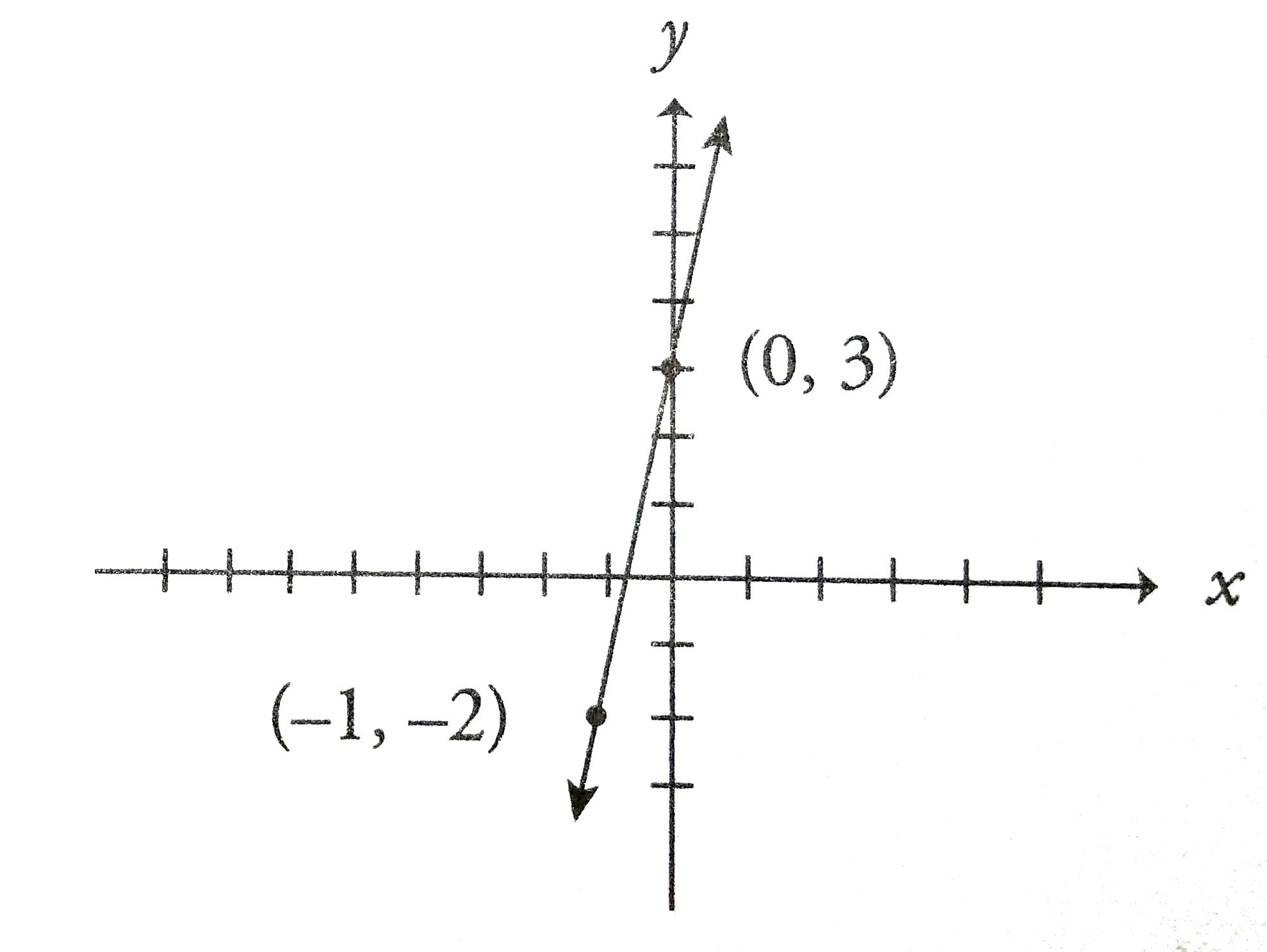
If the graph above is that of f(x), which of the following could be f(x)?
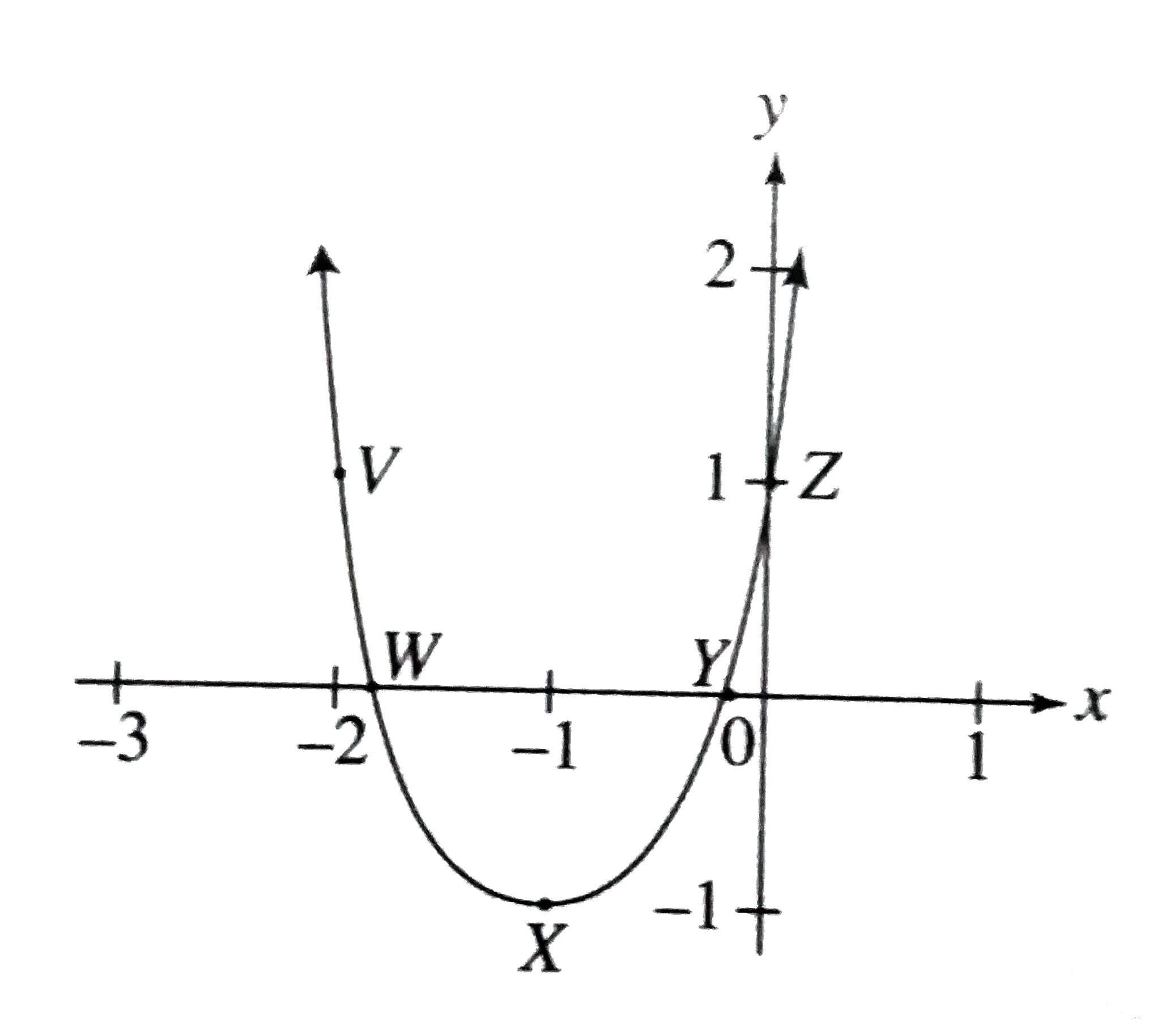
View SolutionThe graph of y=f(x) is shown in the standard (x,y) coordinate plane below with points V,W,X,Y,and Z labeled .
If y=f(x) is to be reflected across the line y=x , which of the following graphs represents the result?
View Solution

