In △JKL,sinL=13,sinJ=35,andJK=√5 inches, the length of KL, is inches, is
1.7
3.0
3.5
4.0
The correct Answer is:D
To find the length of side KL in triangle JKL, we will use the Law of Sines. The Law of Sines states that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant for all three sides of the triangle.
1. Identify the Given Values:
- sinL=13
- sinJ=35
- JK=√5 inches
2. Set Up the Law of Sines:
According to the Law of Sines:
sinJKL=sinLJK
3. Substitute the Known Values:
Substitute the known values into the equation:
35KL=13√5
4. Cross Multiply:
Cross multiplying gives us:
35⋅√5=KL⋅13
5. Solve for KL:
Rearranging the equation to isolate KL:
KL=35⋅√5⋅3
KL=95⋅√5
6. Calculate the Value:
Now, we can calculate KL:
KL≈95⋅2.236(since √5≈2.236)
KL≈9⋅2.2365≈20.1245≈4.025
7. Final Approximation:
Rounding 4.025 gives us approximately 4 inches.
Conclusion:
The length of KL is approximately 4 inches.
---
- sinL=13
- sinJ=35
- JK=√5 inches
According to the Law of Sines:
sinJKL=sinLJK
Substitute the known values into the equation:
35KL=13√5
Cross multiplying gives us:
35⋅√5=KL⋅13
Rearranging the equation to isolate KL:
KL=35⋅√5⋅3
KL=95⋅√5
Now, we can calculate KL:
KL≈95⋅2.236(since √5≈2.236)
KL≈9⋅2.2365≈20.1245≈4.025
Rounding 4.025 gives us approximately 4 inches.
The length of KL is approximately 4 inches.
Topper's Solved these Questions
Similar Questions
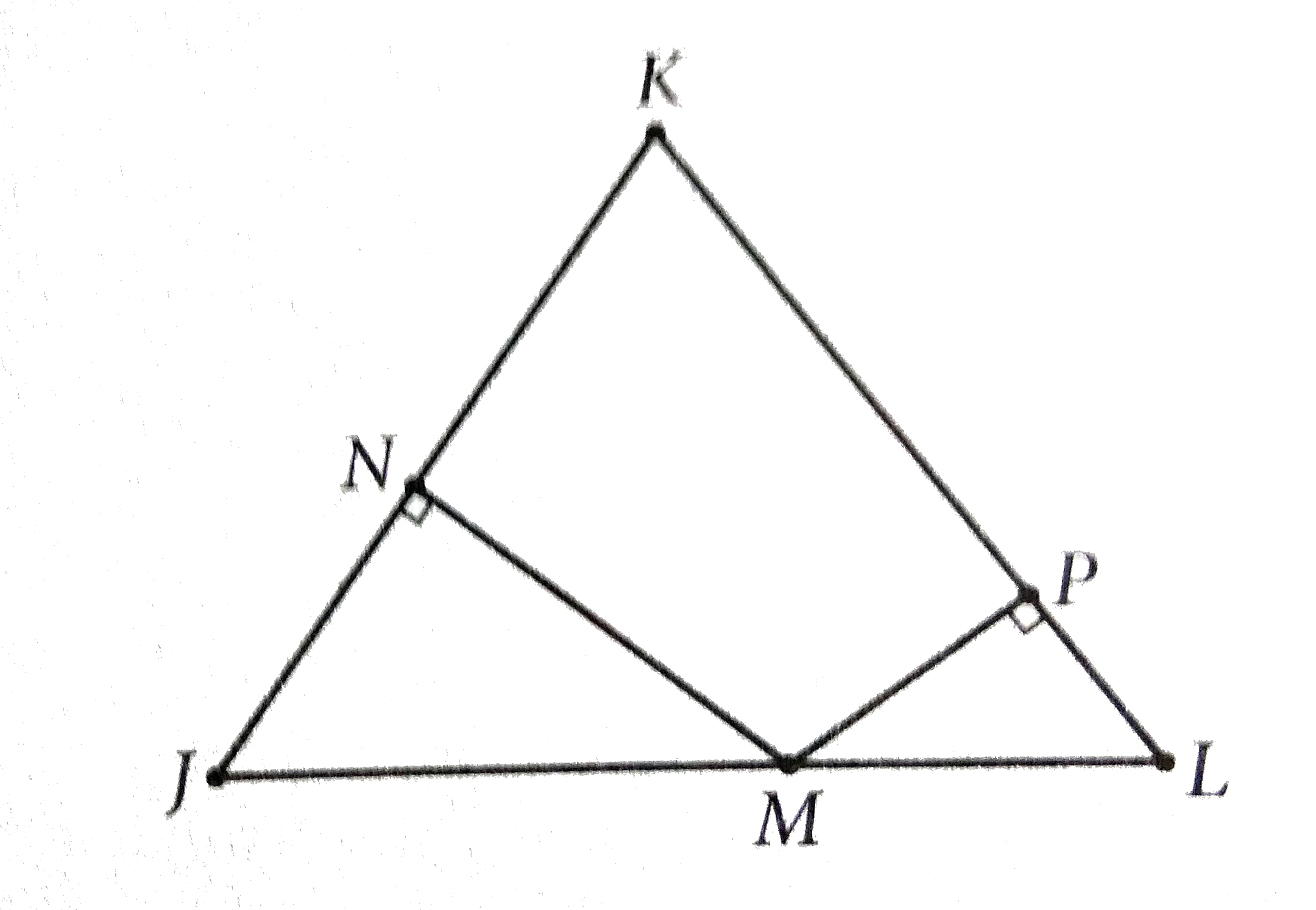
In triangle JKL above, JK=KLandJL=26. The ratio of MN to MP is 8.5. What is the length of segment JM?
View Solution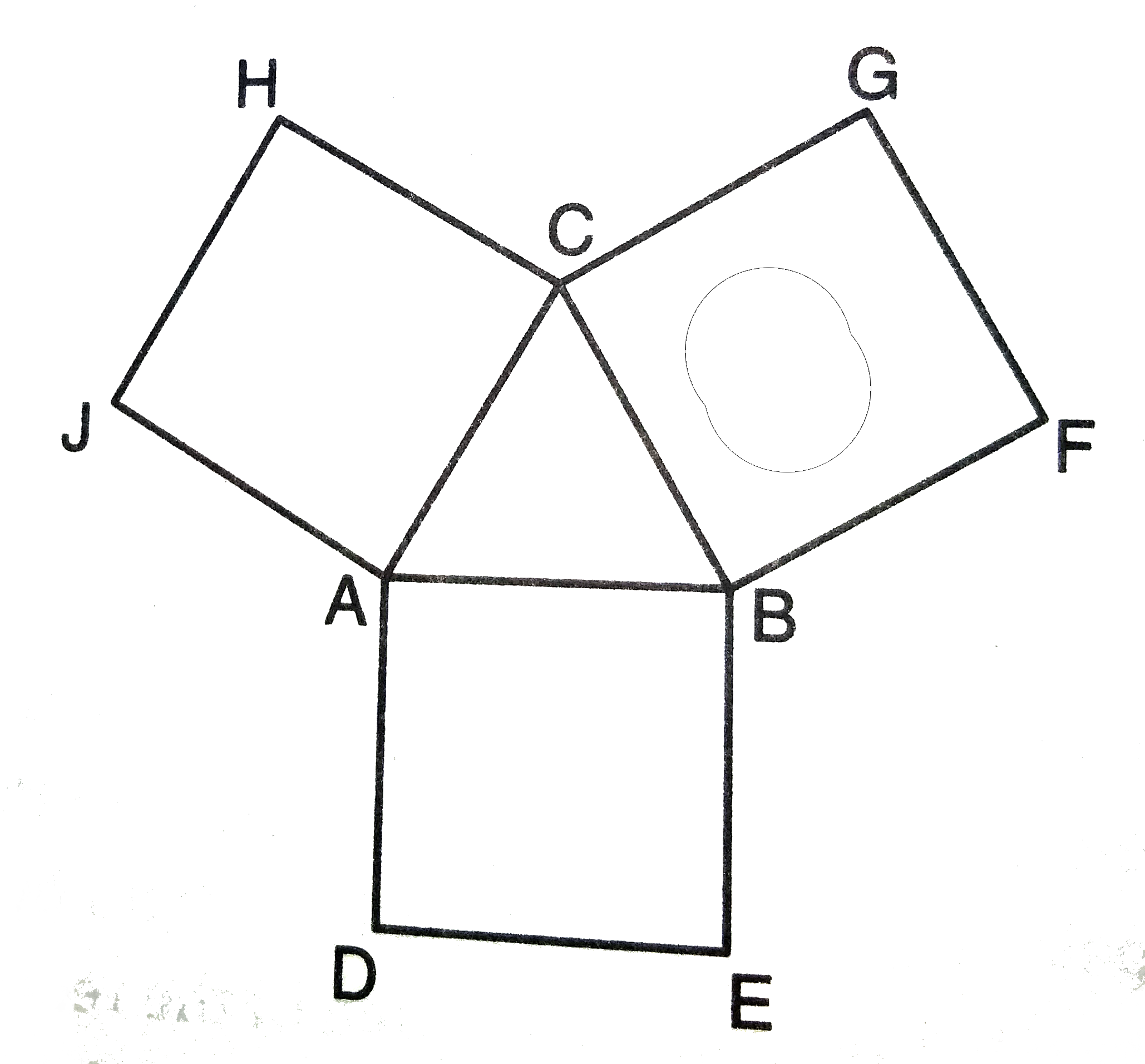
In the figure above, quadrilateral ABED, BFGC, and ACHJ are square. If the area of equilateral △ABC is 16√3 square inches, what is the number of inches in the perimeter of polygon ADEBFGCHJA?
View Solution
Knowledge Check
The area of right triangle is 35 square inches. If the longer leg is 3 inches longer than the shorter leg, what is the length of the hypotenuse, in inches ?
A10B√352C(7√1)D√149When each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a sides of the original square?
A3B4C5D6H = 1.88L + 32.01
The formula above can be used to approximate the height H, in inches, of an adult male based on the length L, in inches, of his femur. What is the meaning of 1.88 in this context?AThe approximate femur length, in inches, for a man with a height of 32.01 inchesBThe approximate increase in a man’s femur length, in inches, for each increase of 32.01 inches in his heightCThe approximate increase in a man’s femur length, in inches, for each one-inch increase in his heightDThe approximate increase in a man’s height, in inches, for each one-inch increase in his femur length
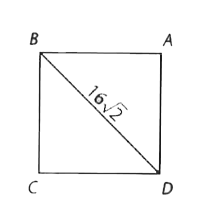
A square is bisected into two triangles (see figure). If the length of BD is 16√2 inches, what is the area of the square?
View SolutionA pentagon has three sides with length x, and two sides with the length 3x. If x is 23 of an inch, what is the perimeter of the pentagon?
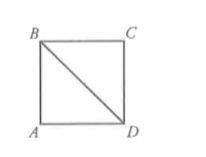
View SolutionA square is bisected into two equal triangle (see figure). If the length of BD is 16sqrt2 inches, what is the area of the square?
View SolutionIf the extremities of the diagonal fo a square are (1,-2,3) and (2,-3,5), then the length of the side is √6 b. √3 c. √5 d. √7
View SolutionA parallelogram has a perimeter of 96 inches, and 1 of its sides measures 16 inches. If it can be determined. What are the lengths, in inches, of the other 3 sides?
View Solution
