A man uses a concave mirror for shaving and see his 2 times enlarged image when his face is at a distance 40 cm from mirror.Find focal length of mirror
[80 cm]
To find the focal length of the concave mirror used by the man for shaving, we can follow these steps:
Step 1: Understand the given information
- The object distance (U) is given as -40 cm (the negative sign indicates that the object is in front of the mirror).
- The magnification (m) is given as 2 (the image is twice the size of the object).
Step 2: Use the magnification formula
The magnification (m) for mirrors is given by the formula:
m=−VU
Where:
- V is the image distance.
- U is the object distance.
Step 3: Substitute the known values into the magnification formula
We know:
m=2
U=−40cm
Substituting these values into the magnification formula:
2=−V−40
This simplifies to:
2=V40
Step 4: Solve for the image distance (V)
To find V, we can rearrange the equation:
V=2×40=80cm
Step 5: Apply the mirror formula
The mirror formula is given by:
1F=1V+1U
Where:
- F is the focal length.
- V=80cm (positive because the image is real and on the same side as the object for a concave mirror).
- U=−40cm.
Step 6: Substitute the values into the mirror formula
Substituting the values we have:
1F=180+1−40
Step 7: Simplify the equation
To simplify:
1F=180−280
1F=1−280
1F=−180
Step 8: Find the focal length (F)
Taking the reciprocal gives:
F=−80cm
Conclusion
The focal length of the concave mirror is −80cm.
---
- The object distance (U) is given as -40 cm (the negative sign indicates that the object is in front of the mirror).
- The magnification (m) is given as 2 (the image is twice the size of the object).
The magnification (m) for mirrors is given by the formula:
m=−VU
Where:
- V is the image distance.
- U is the object distance.
We know:
m=2
U=−40cm
2=−V−40
This simplifies to:
2=V40
To find V, we can rearrange the equation:
V=2×40=80cm
The mirror formula is given by:
1F=1V+1U
Where:
- F is the focal length.
- V=80cm (positive because the image is real and on the same side as the object for a concave mirror).
- U=−40cm.
Substituting the values we have:
1F=180+1−40
To simplify:
1F=180−280
1F=1−280
1F=−180
Taking the reciprocal gives:
F=−80cm
The focal length of the concave mirror is −80cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Practive Exercise 5.3
12 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Practive Exercise 5.4
11 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Practive Exercise 5.1
10 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
Similar Questions
An object is placed in front of a concave mirror at a distance of 7.5 cm from it. If the real image is formed at a distance of 30 cm from the mirror, find the focal length of the mirror. What would be the focal length if the image is virtual.
View SolutionA man uses a concave mirror for shaving. He keeps his face at a distance of 25 cm from the mirror and gets an image which is 1.4 times enlarged. Find the focal lengt.1 of the mirror
View Solution
Knowledge Check
An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
A15 cmB45 cmC30 cmD20 cmFor a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
Af2B3f2Cf4D4f3Image formed by a concave mirror of focal length 6 cm , is 3 times of the object, then the distance of object from mirror is
A−4cmB8cmC6cmD12cm
A man uses a concave mirror for shaving. He keeps his face at a distance of 20cm form the mirror and gets an image which is 1.5 times entarged. Find the focal length of the mirror.
View SolutionConcave mirror forms the real image of a point source lying on the optical axis at a distance of 50 cm from the mirror. The focal length of the mirror is 25 cm. The mirror is cut into and its halves are drawn a distance of 1 cm apart in a direction perpendicular to the optical axis. How will the image formed by the halves of the mirror be arranged?
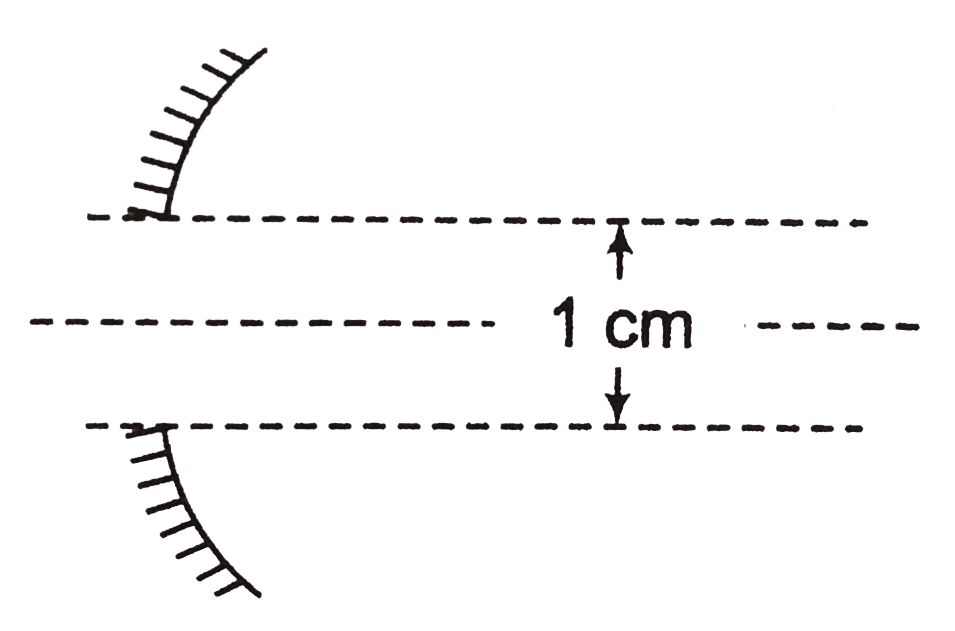
View SolutionA concave mirror of focal length 'f' forms an erect image twice the size of an object. Find the object distance from the mirror.
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cmfrom it.Focal length of mirror is20cm
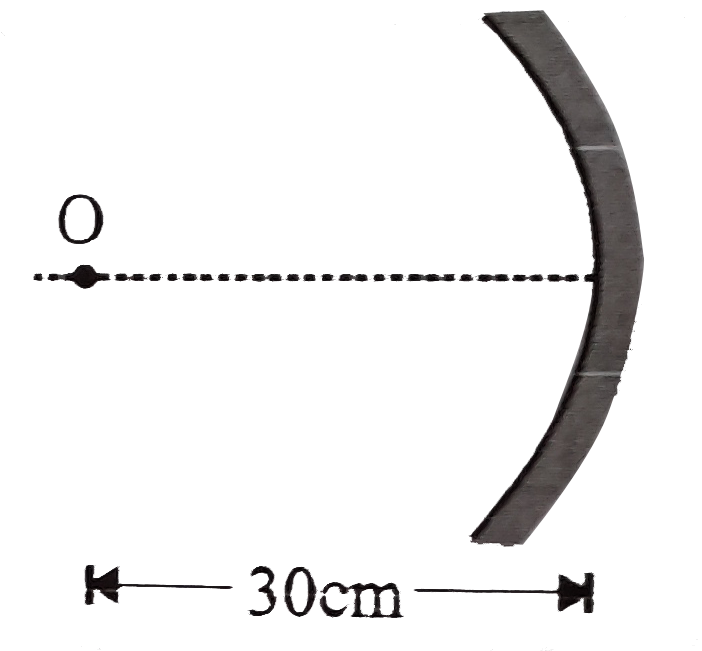
Image formed by mirror is
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
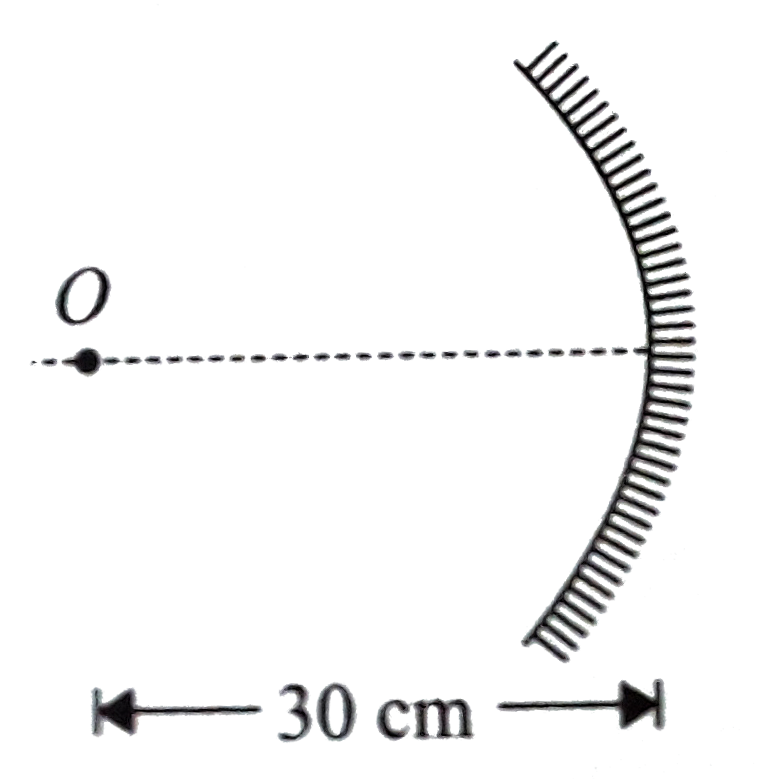
Q. Image formed by mirror is
View Solution