Two particle 'A' and 'B' are moving on the same circle with angular ω1 and ω2 respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when,
(i) their sense of rotations is same,
(ii) and their sense of rotation is opposite.

Step by step video & image solution for Two particle 'A' and 'B' are moving on the same circle with angular omega_(1) and omega_(2) respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when, (i) their sense of rotations is same, (ii) and their sense of rotation is opposite. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example95videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - level 1103videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
Knowledge Check
- Question 1 - Select One
Buses A and B are moving in the same direction with speed 20ms−1 and 15ms−1 respectively. Find the relative velcoity of A w.r.t. B and relative velocity of B w.r.t. A.
A(15ms−1)ˆi (−5ms−1)ˆiB(5ms−1)ˆi (−15ms−1)ˆiC(5ms−1)ˆi (−5ms−1)ˆiD(5ms−1)ˆi (15ms−1)ˆi - Question 1 - Select One
A and B are moving in two circular orbits with angular velocity
2ωandω respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time
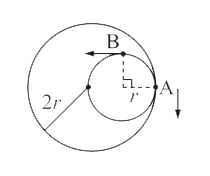 Aπ2ωB3π2ωCπωDThey will never meet
Aπ2ωB3π2ωCπωDThey will never meet - Question 1 - Select One
Two objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
AvA−vBBvA+vBCvB−vADvA/vB - Question 1 - Select One
A particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
A2ωBω2CωDNot constant - Question 1 - Select One
If I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
Aτ=IαBτ=I.ωCτ=I/ωDα=τ.ω
Similar Questions
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
 View Solution
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
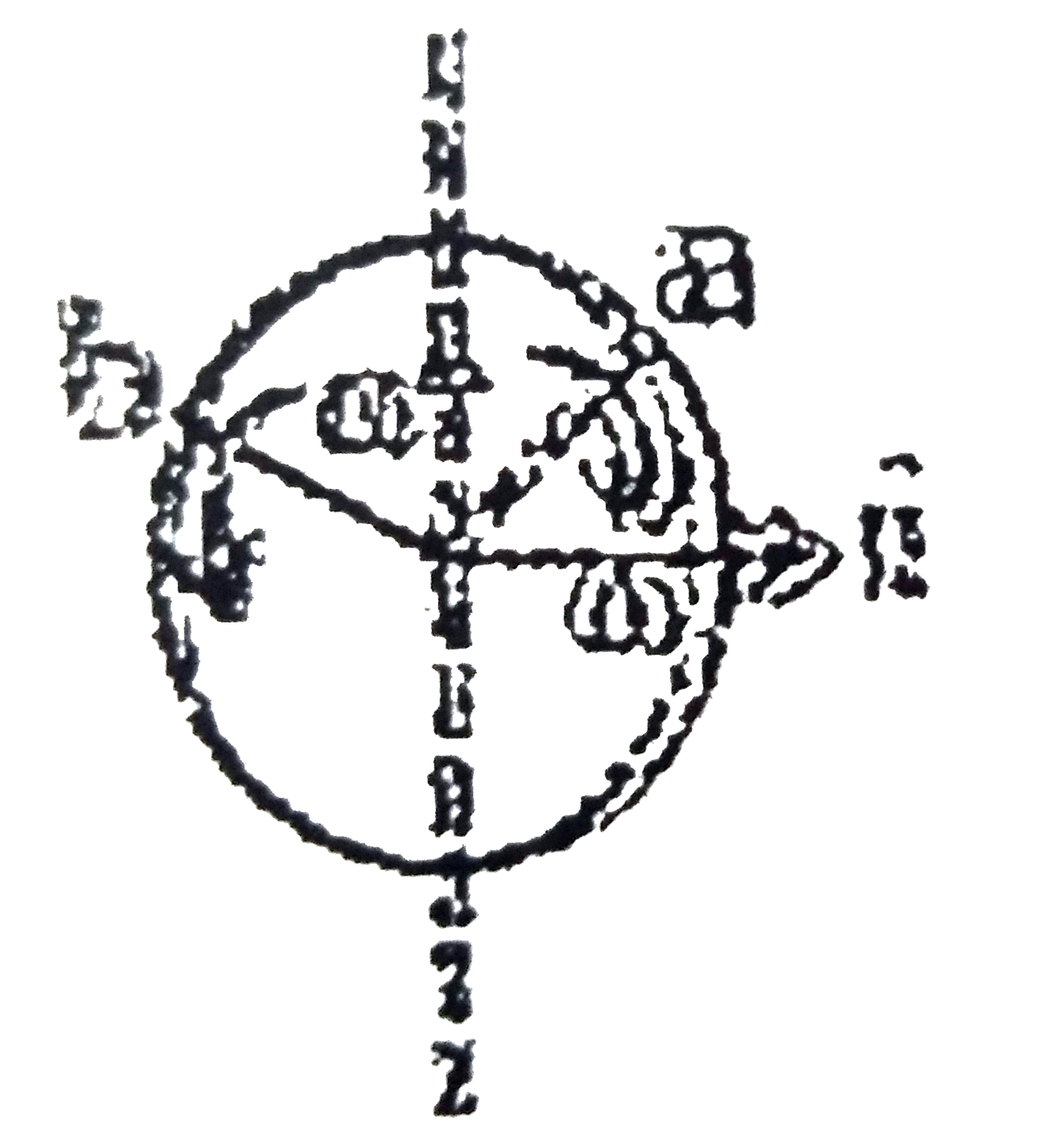
View SolutionParticles a and b move in opposite direction around a circle with same angular speed ω, as shown. At t=0 they are both at the point →r=→t→j, where l is the radius of the circle. The magnitude angular velocity of 'a' w.r.t. 'b' at time t=t
 View Solution
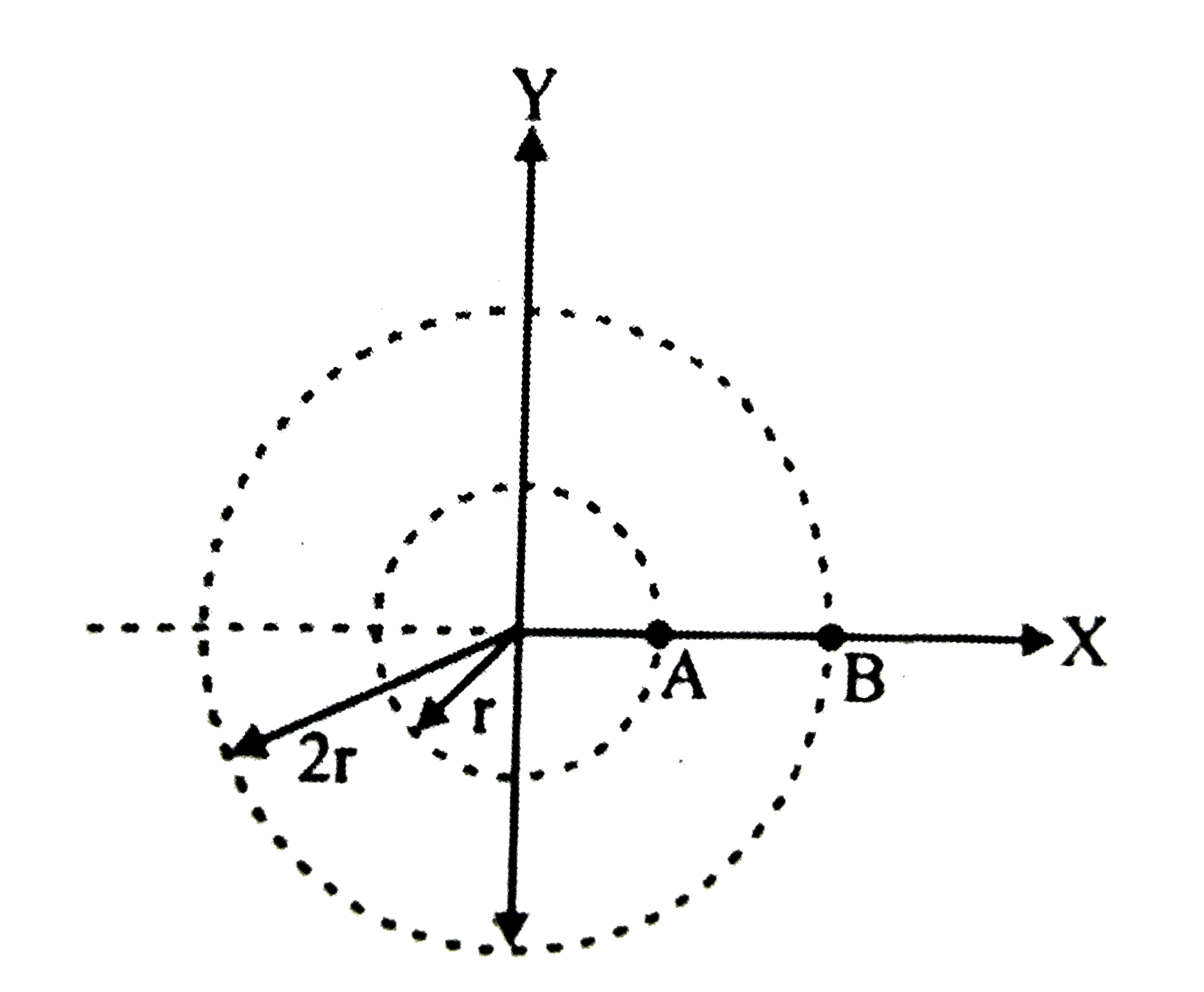
View SolutionTwo particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2ω and ω respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=π/ω. They both start at the position as shown in figure (Takeω=3rad/sec,r=2m)
 View Solution
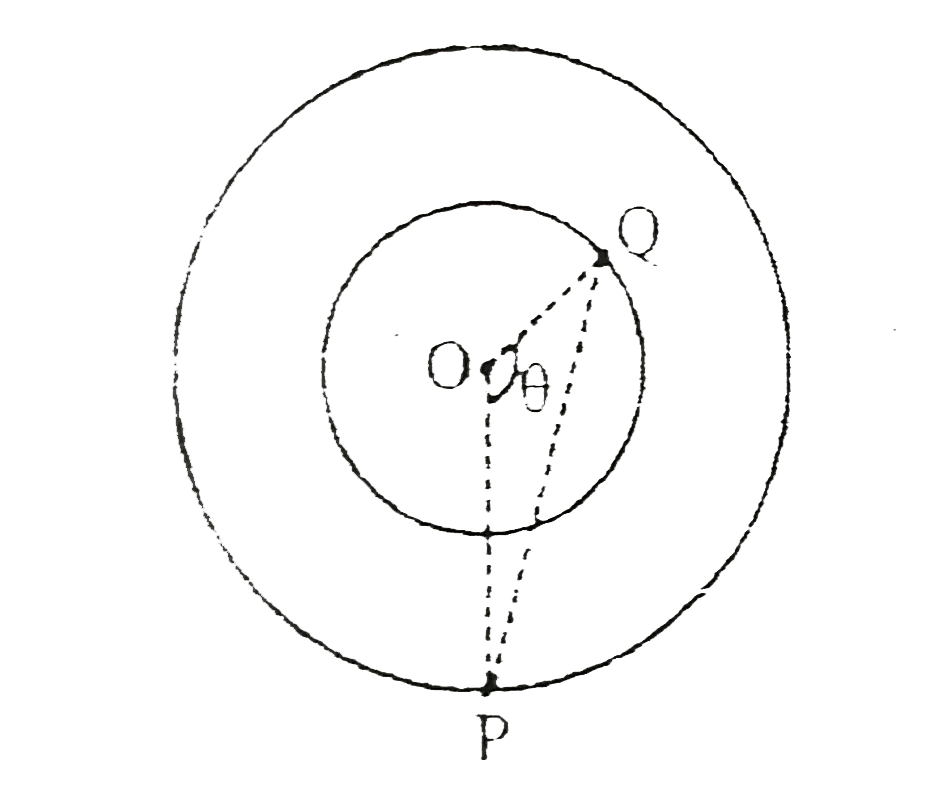
View SolutionTwo particles P and Q describe coplanar concentric circles of radii a and a' with angular velocities ω and ω', (in the same sense ) respectively. If the angular velocity of P with respect to Q is x, then fill 49x12 in OMR sheet. Take θ=2π3,a=2m,a'=1m,ω=2rad/s &ω'=1rad/s.
 View Solution
View Solution

