A square loop of side 'l' each side having uniform linear charge density 'lambda' is placed in 'xy' lane as shown in the figure There exists a non uniform electric field →E=al(x+l)ˆi where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons) if l=10cmλ=20μC/manda=5×105N/C.
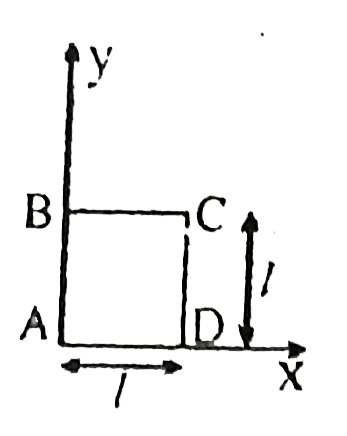
Step by step video & image solution for A square loop of side 'l' each side having uniform linear charge density 'lambda' is placed in 'xy' lane as shown in the figure There exists a non uniform electric field vec(E)=a/l(x+l)hat(i) where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons) if l=10 cm lambda=20 muC//m and a=5 xx 10^(5) N//C. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.2
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.3
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.1
Explore 1 Video
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:Advance MCQs
Explore 33 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
Similar Questions
A square loop of side l having uniform linear charge density λ is placed in an x−y plane as shown in the figure. There is a non-uniform electric field E=al(x+l)→i, where a and l are constants. The resultant electric force on the loop is having the value 2naλ. Find the value of n.
'(##CEN_KSR_PHY_JEE_C18_E01_032_Q17##)'
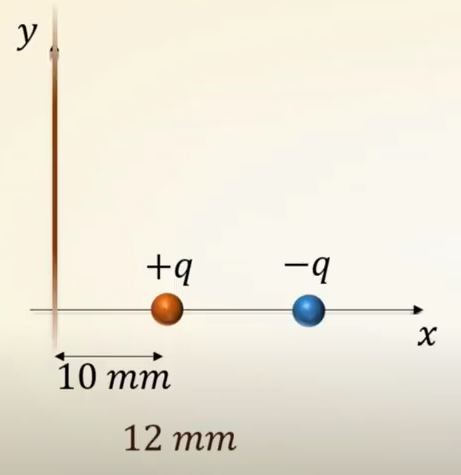
View SolutionA line charge having a linear charge density of 3×10−6Cm is placed as shown in figure. A dipole is placed on x-axis as shown. Find the charge q if it is subjected to a force of 4N.
View Solution
Knowledge Check
A square loop of side 'l' having uniform linear charge density 'λ' is placed in 'xy' plane as shown in the figure. There is a non uniform electric field →E=al(x+l)ˆi where a is a constant. Then resultant electric force on the loop if l=10cm,a=2N/C and charge density λ=2μC/m is:
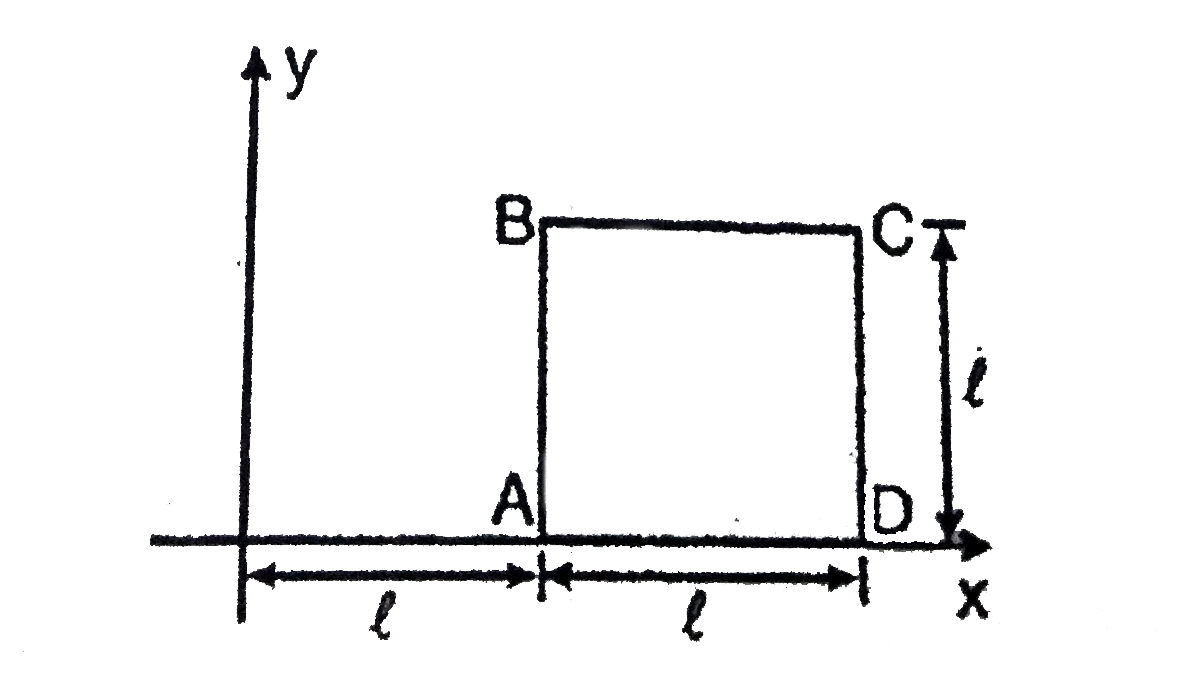 A4×10−6NB4×10−5NC3×10−6ND3×10−5N
A4×10−6NB4×10−5NC3×10−6ND3×10−5NA square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
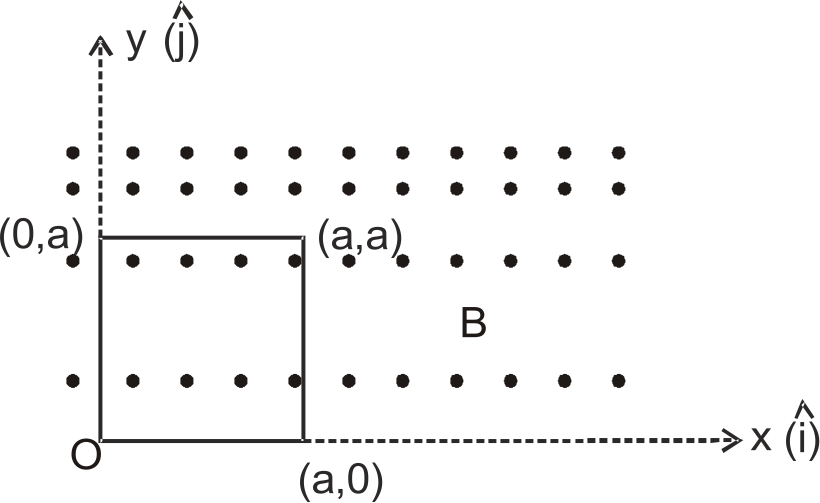 AZeroBca4t25Cca5t2Ddata is insufficient
AZeroBca4t25Cca5t2Ddata is insufficientA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
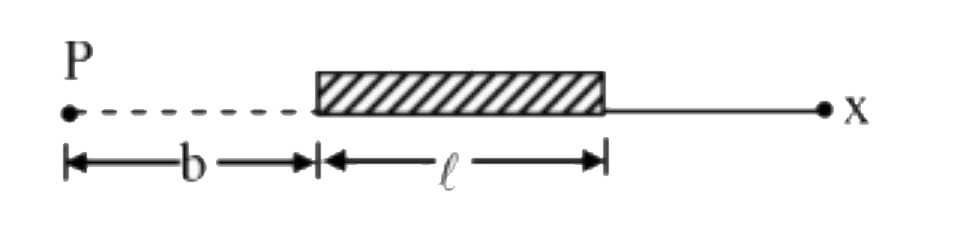 AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
A non-uniform electric field E=(5xˆi+3ˆj)NC goes through a cube of side length 2.0m oriented as shown. Then,
View SolutionA cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m.
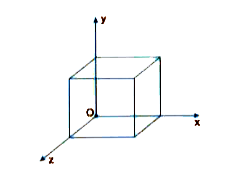
Find the
(i) electric field →E, and
(ii) total electric flux through the cube.
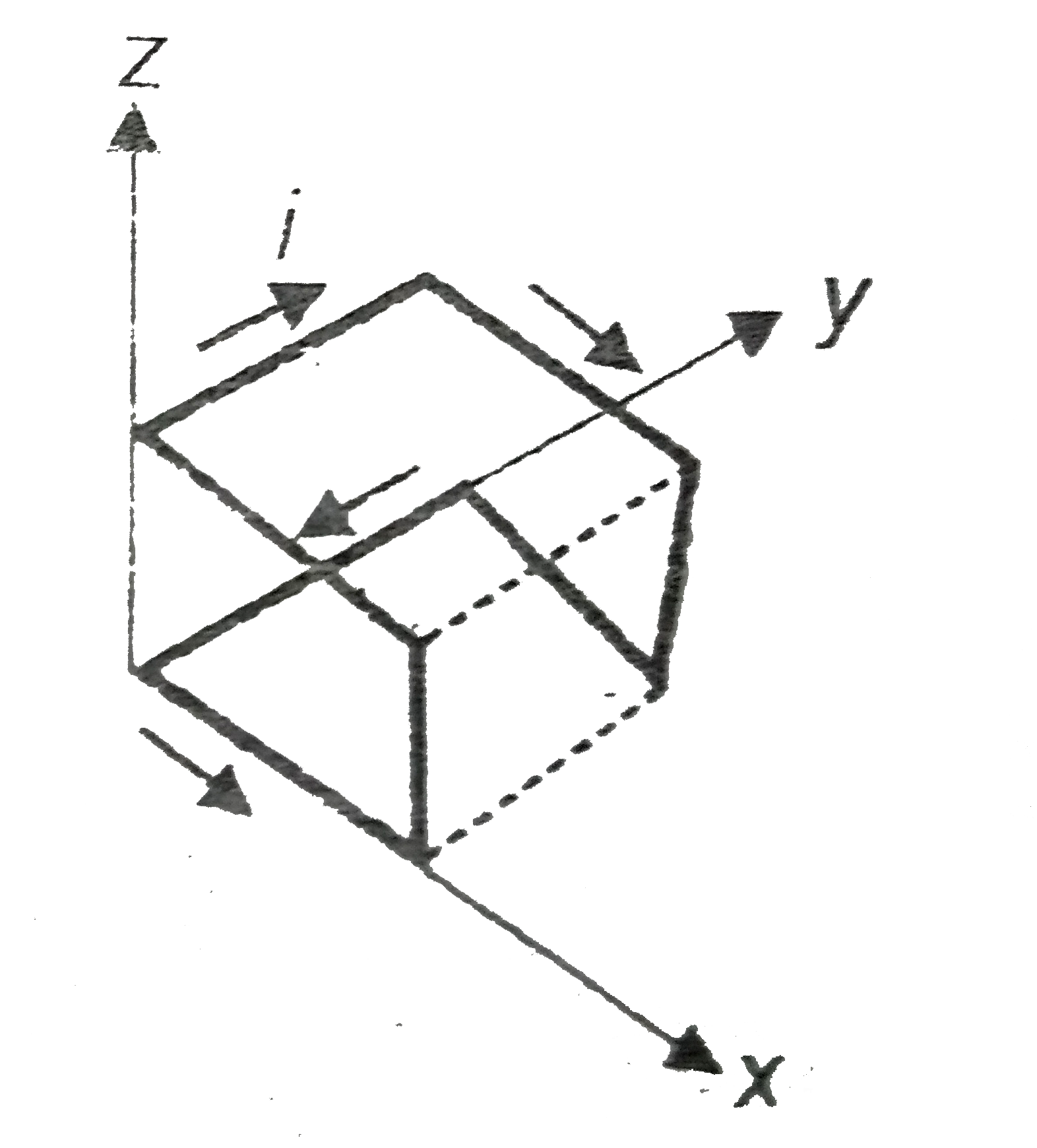
View SolutionThe figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by →B=B0ˆi. If the length of each side is a, then
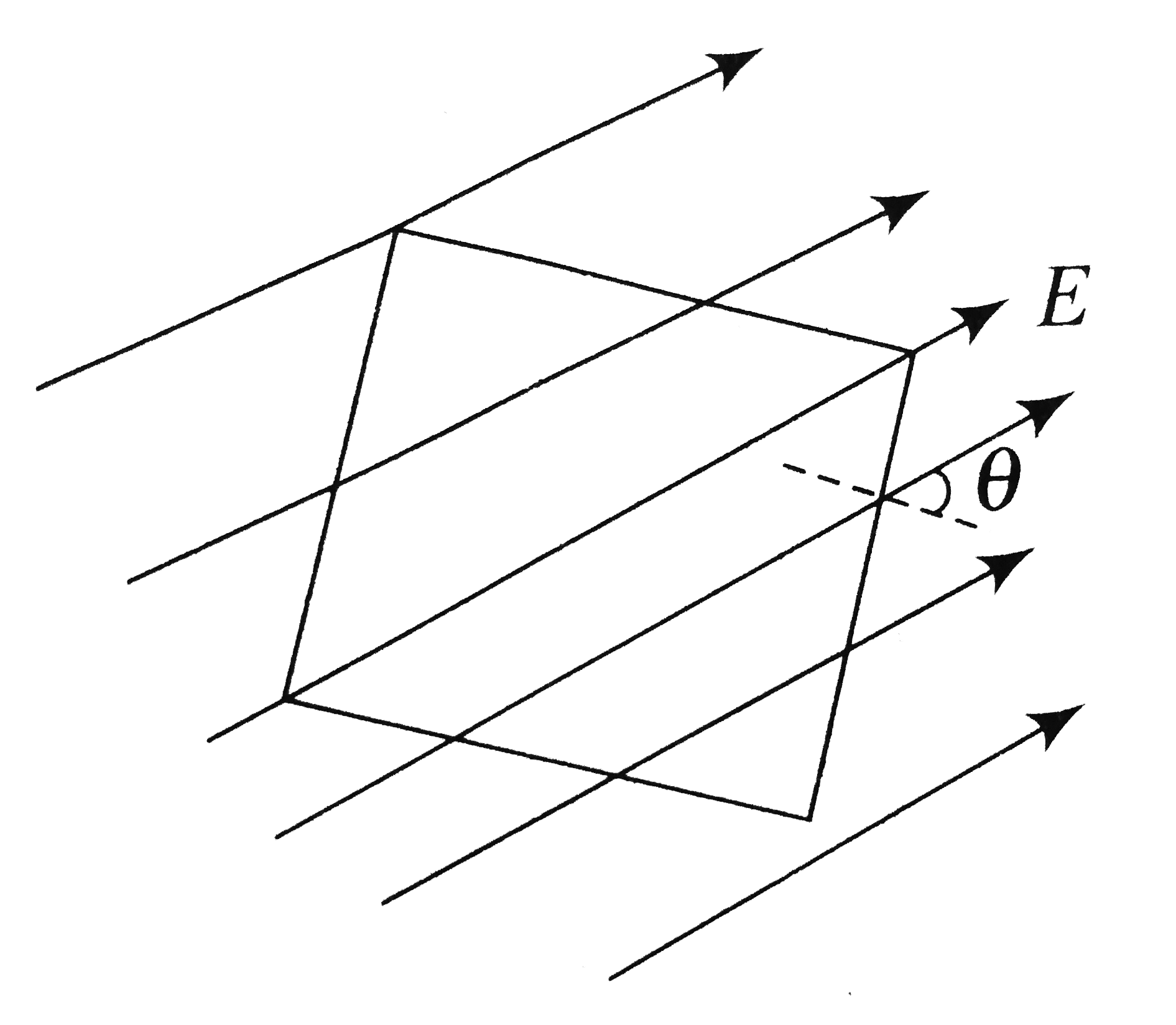
View SolutionA square surface of side L in the plane of the paper is placed in a uniform electric field E acting along the same. Plane at an angle θ with the horizontal side of the square as shown in. The electric flux linked to the surface is

View SolutionA square surface of side L metre in the plane of the paper is placed in a uniform electric field E(volt/m) acting along the same place at an anlge θ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of V−m is
View Solution

