An infinitely long cylindrical surface density σ=σ0cosφ. Where φ is the polar angle of the cylindrical coordinate system whose z axis coincides with the axis of the given surface. Find the magnitude and direction of the electric field strength vector on the z axis.
Step by step video & image solution for An infinitely long cylindrical surface density sigma = sigma_(0) cos varphi. Where varphi is the polar angle of the cylindrical coordinate system whose z axis coincides with the axis of the given surface. Find the magnitude and direction of the electric field strength vector on the z axis. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.1
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise
Explore 93 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:Advance MCQs
Explore 33 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
Similar Questions
An infineltly long cylindrical surface density σ=σ0cosφ. Where φ is the polar angle of the cylindrical coordinate system whose z axis coincides with the axis of the given surface. Find the magnitude and direction of the electric fiels strength vector on the z axis.
View SolutionWhen an uncharged conducting ball of radius R is placed in an external uniform electric field, a surface charge densityh σ=σ0cosθ is induced on the ball's surface charge (here σ0 is a constant, θ is a polar angle). Find the magnitude of the resultant electric force acting on an induced charge of the same sign.
View Solution
Knowledge Check
An infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
AzeroBanticlockwise of the +ve z axisCclockwise of the +ve z axisDalong the magnetic fieldTwo infinitely long parallel sheets having surface charge densities +σand−σ respectively are separated by a small distance. The electric field in the region between the plates is
A0Bσ2∈0Cσ∈0D2σ∈0
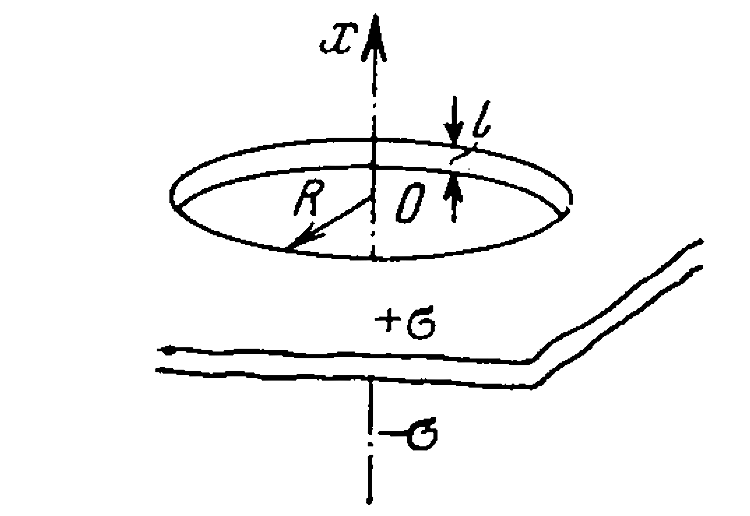
Two infinite planes sepated by a distance l carrying a uniform surface charge of densities σ and −σ. The planes have round coaxial holes of radius R, with l<<R. Taking the origin O and the x cordinates axis as shown in the figure, find the potentail of the electric field and the projection of its strength vector Ex on the area of the system as functions of the x cordiante. Draw the appoximate plot φ(x).
View SolutionIn a long insulating cylinder of radius R a cylindrical tunnel of radius a located at a distance b from the axis of the cylinder as shown in the figure. R R b - The solid part of the cylinder has a uniform volume charge density P. Find the magnitude and direction of the electric field inside the tunnel.
View SolutionA thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius r and length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionState Gauss' law in electrostatic.. A thin straight infinitely long conducting wire of linear charge density λ is enclosed by a cylinder surface of radius 'r' and length ''l' ,its axis coinciding with the length of the wire . Qbtain the expressionn for the electric field, indicating its direction at a point on the surface of the cylinder.
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA thin straight infinitely long conducting wire having charge density λ is enclosed by a cylinder surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View Solution