Three resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
Step by step video & image solution for Three resistors having resistances of 1.60 Omega, 2.40 Omega and 4.80 Omega are connected in parallel to a 28.0 V battery that has negligible internal resistance. Find (a) the equivalent resistance of the combination. (b) the current in each resistor. (c) the total current through the battery. (d) the voltage across each resistor. (e) the power dissipated in each resistor. (f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
A2019ΩB1920ΩC1910ΩD1019ΩThree resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4, 3, 2.4B8, 7, 3.4C2, 5, 1.8D5, 5, 8.2Three resistors of resistance 2Ω,5Ω and 3Ω respectively are connected in parallel across a battery of 10 volts and negligible resistance. The potential difference across 5 Ω resistor is
A5VB2VC3VD10V
Two resistors 4Ωand6Ω connected in parallel. The combination is connected across a 6V battery of negligible resistance. Calculate
(a) the current through the battery
(b) current through each resistor.
View SolutionThree resistors of 1Ω,2Ωand3Ω are connected in parallel. The combined resistance of 3 resistors should be
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
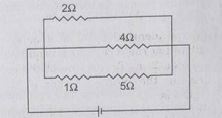
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is

View SolutionA current of 3 A flows through the 2Ω resistor shown in the circuit. The power dissipated in the 5 Ω resistor is

View Solution