A μF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
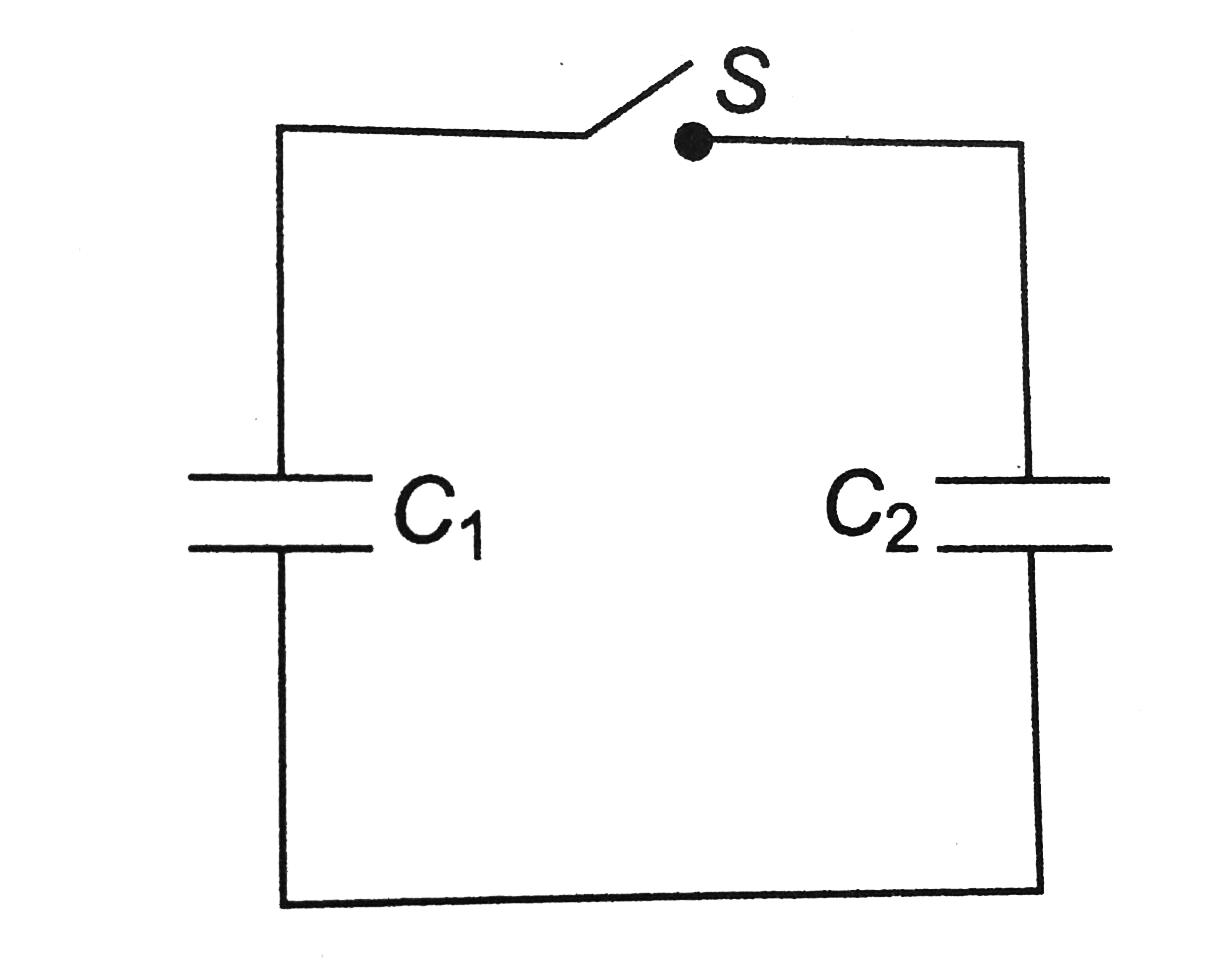
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
Step by step video & image solution for A muF capacitor C_1 is charged to V_0 = 120 V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged + 4muF capacitor C_2. (a) what is the potential difference V across the combination? (b) what is the stored energy before and after the switch S is closed? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CAPACITANCEBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CAPACITANCEEXERCISE - DISCUSSION QUESTIONS
22 Videos
- CAPACITANCEBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CAPACITANCEEXERCISE - CONCEPTUAL MCQA
32 Videos
- ATOMIC PHYSICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Unsolved Numerical Problems
39 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
Similar Questions
A 2μF capacitor is connected to a 10 V battery. What is the electrostatic energy stored in the capacitor?
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate cap the capacity of second capacitor.
View Solution
Knowledge Check
A capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
AVC1C1+C2BVC2C1+C2CVC1C2C1+C2DVC1+C2A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1A capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
AC(V0−V)VBC(V−V0)VCCVV0DCV0V
A 2μF capacitor C1 is first charged to a potential difference of 10 V using a battery. Then the battery is removed and the capacitor is connected to an uncharged capacitor C2 of 8μF. The charge in C2 on equilibrium condition is _______μC. (Round off to the Nearest Integer)
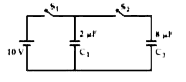
View SolutionA 10μF capacitor is charged to a potential difference of 1000V. The terminals of the charged capacitor are disconnected from the power supply and connected to the terminals of an uncharged 6μF capacitor. What is the final potential difference across each capacitor ?
View SolutionA 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply . And is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation ?
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View Solution
