A particle is moving along an expanding spiral in such a manner that the particle's normal acceleration remains constant. How will the linear and angular velocities change in the process?
To solve the problem, we need to analyze the motion of a particle moving along an expanding spiral while maintaining constant normal acceleration. Let's break this down step by step.
Step 1: Understanding Normal Acceleration
The normal acceleration An of a particle moving in a circular path is given by the formula:
An=V2R
where V is the linear velocity and R is the radius of the spiral.
Step 2: Relating Normal Acceleration to Linear Velocity
Since the problem states that the normal acceleration is constant, we can express the relationship between linear velocity and radius:
V2=An⋅R
Taking the square root gives us:
V=√An⋅R
Step 3: Analyzing the Relationship Between Linear Velocity and Radius
From the equation V=√An⋅R, we can see that as the radius R increases (since the spiral is expanding), the linear velocity V must also increase because An is constant.
Step 4: Understanding Angular Velocity
We can also relate angular velocity ω to linear velocity and radius using the formula:
V=R⋅ω
Rearranging this gives:
ω=VR
Step 5: Substituting for Linear Velocity
Substituting V=√An⋅R into the angular velocity equation gives:
ω=√An⋅RR=√An√R
This indicates that angular velocity ω is inversely proportional to the square root of the radius R.
Step 6: Conclusion on Changes in Velocities
- As the radius R increases, the linear velocity V increases because V is proportional to √R.
- Conversely, the angular velocity ω decreases because ω is inversely proportional to √R.
Final Result
In summary:
- The linear velocity V increases as the radius R increases.
- The angular velocity ω decreases as the radius R increases.
The normal acceleration An of a particle moving in a circular path is given by the formula:
An=V2R
where V is the linear velocity and R is the radius of the spiral.
Since the problem states that the normal acceleration is constant, we can express the relationship between linear velocity and radius:
V2=An⋅R
Taking the square root gives us:
V=√An⋅R
From the equation V=√An⋅R, we can see that as the radius R increases (since the spiral is expanding), the linear velocity V must also increase because An is constant.
We can also relate angular velocity ω to linear velocity and radius using the formula:
V=R⋅ω
Rearranging this gives:
ω=VR
Substituting V=√An⋅R into the angular velocity equation gives:
ω=√An⋅RR=√An√R
This indicates that angular velocity ω is inversely proportional to the square root of the radius R.
- As the radius R increases, the linear velocity V increases because V is proportional to √R.
- Conversely, the angular velocity ω decreases because ω is inversely proportional to √R.
In summary:
- The linear velocity V increases as the radius R increases.
- The angular velocity ω decreases as the radius R increases.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle is moving in a circle with a constant speed, the acceleration of the particle has
Aconstant magnitudeBconstant magnitude and directionCboth magnitude and direction changesDneither magnitude nor direction changesA particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is
Arω2Br/ωCzeroDω/rThe figure shows a particle moving along x - axis subjected to three particles of acceleration (a). Rank the periods according to the increase they produce in the particle velocity, greatest first.
 A
A B
B C
C D
D
A particle is moving horizontally with constant acceleration.
View SolutionA particle is moving along an elliptical path with a constant speed. As it moves from A to B, magnitude of its acceleration:
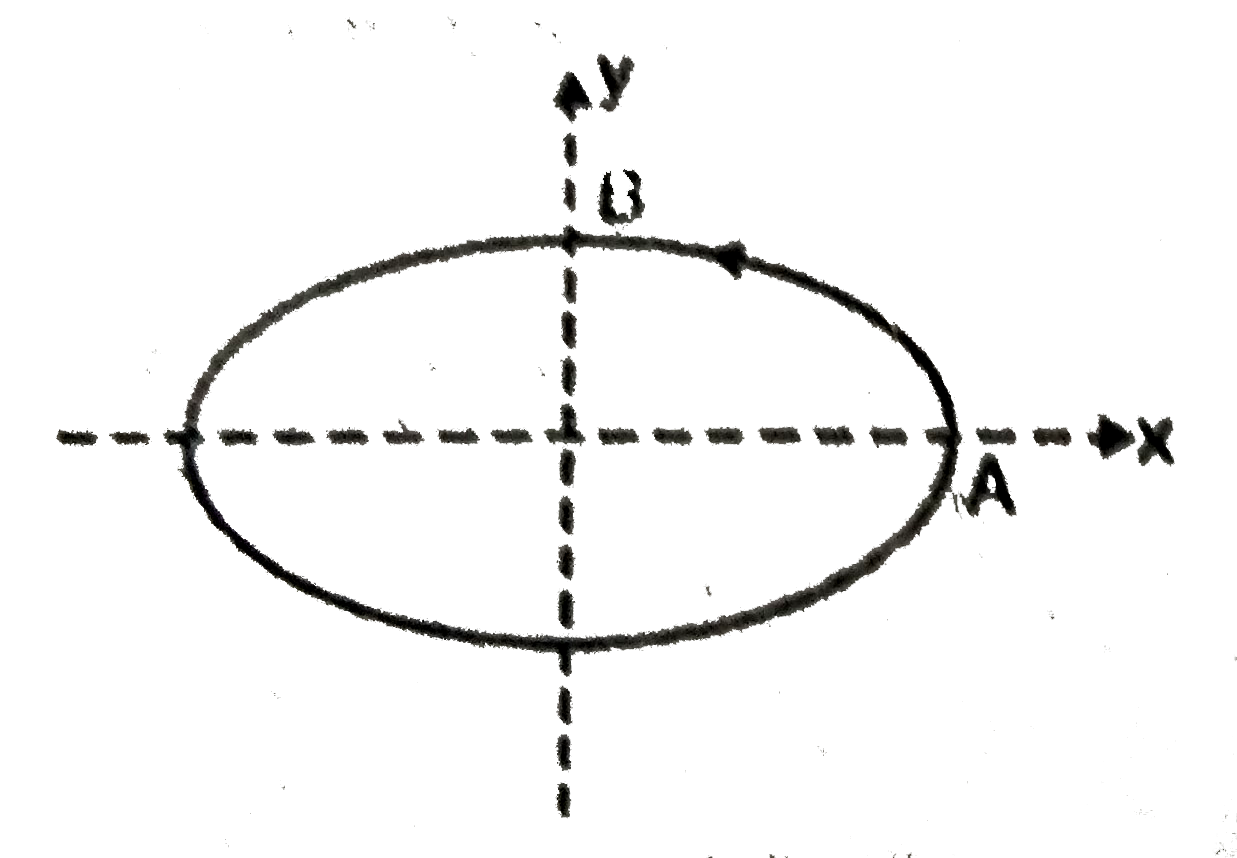
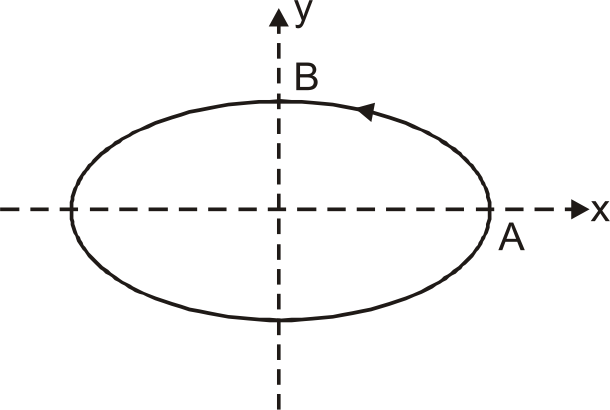
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
View SolutionAssertion : Acceleration of the particle in uniform circular motion remain constant.
Reason : Velocity of the particle doesn’t change in circular motion.
View SolutionA particle moves along a circule path with a constant angular velocity. This necessarily means that the motion
View Solution
