A particle of mass m undergoes oscillations about x = 0 in a potential given by V(x)=12kx2−v0cos(xa), where V0,K,a are constants. If the amplitude of oscillation is much smaller than a, the time period is given by-
2π√ma2ka2+V0
2π√mk
2π√ma2V0
2π√ma2ka2−V0
Step by step video & image solution for A particle of mass m undergoes oscillations about x = 0 in a potential given by V(x)=(1)/(2)kx^(2)-v_(0)cos((x)/(a)), where V_(0),K,a are constants. If the amplitude of oscillation is much smaller than a, the time period is given by- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
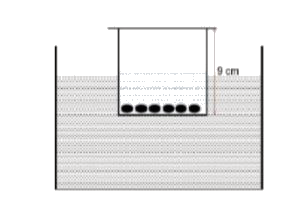
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is V(x)=k|x|3 where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|^(2) , where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionA particle of mass m is executing oscillation about the origin on X- axis Its potential energy is V(x)=kIxI Where K is a positive constant If the amplitude oscillation is a, then its time period T is proportional
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x) = 0 [1 - cos ax] , where U_(0) and a are constants. The time period of small oscillations of the particle about the mean positions is :
View Solutionm द्रव्यमान का एक कण X-अक्ष पर मूलबिंदु के परितः दोलन कर रहा है इसकी स्थितिज ऊर्जा U(x)=k|x|3 है जहाँ K एक धन नियतांक है यदि दोलन का आयाम a है तब इसका आवर्तकाल T :
View SolutionThe position x of a particle at time t is given by : x=(v_(0))/(a)(1-e^(-at)) where v_(0) is a constant and a>0. The dimensional formula of v_(0) and a is :
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis. Its potential energy is V(x)=kx^(2) . Where k is a positive constant. If the amplitude of oscillation is a, then its time period T is……………
View SolutionA body of mass m is situated in a potential field U(x) = V0(1−cosax) when U0 and α are constants. Find the time period of small oscillations.
View SolutionThe position x of a particle at time t is given by x=V0a(1−e−at), where V0 is constant and a>0. The dimensions of V0 and a are
View SolutionA particle of mass m oscillates with a potential energy U=U_(0)+alpha x^(2) , where U_(0) and alpha are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View SolutionThe position x of a particle at time t is given by x=V0a(1−e−at), where V0 is constant and a>0. The dimensions of V0 and a are
View SolutionA particle of mass m is executing oscillations about the origin on X-axis. Its potential energy isU(x)=−K|x|3, where K is a positive constant. If the amplitude of oscillation is a, then its time period T is:
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is V(x)=k|x|3 where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View Solution
