A negative charge Q is distributed uniformly in volume of a sphere is radius R and a point charge particle (may be negative or positive) is present on the surface of this sphere then variation of escape velocity (vs) of charge 'q' as a function of 'q' will be [neglect gravitational interaction].
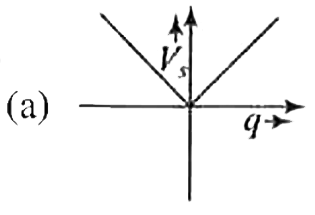

The correct Answer is:C
To solve the problem of finding the variation of escape velocity vs of a charge q as a function of q when a negative charge Q is uniformly distributed in a sphere of radius R, we can follow these steps:
Step 1: Understanding the System
We have a uniformly distributed negative charge Q within a sphere of radius R. A point charge q is located on the surface of this sphere. We need to determine how the escape velocity vs of the charge q varies with q.
Step 2: Use Energy Conservation
The principle of conservation of mechanical energy states that the total mechanical energy at the initial point (when the charge is at the surface) must equal the total mechanical energy at the point of escape (where the potential energy is zero).
The equation can be written as:
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
Step 3: Write the Energy Equation
Initially, when the charge q is at the surface of the sphere, its kinetic energy is 12mv2s and the potential energy due to the charge Q is given by:
Ui=−kQqR
where k is Coulomb's constant. At the point of escape, the kinetic energy is 0 and the potential energy is also 0.
Thus, we can write:
12mv2s−kQqR=0
Step 4: Rearranging the Equation
Rearranging the equation gives us:
12mv2s=kQqR
Multiplying both sides by 2 leads to:
mv2s=2kQqR
Step 5: Solve for Escape Velocity vs
Now, we can solve for the escape velocity vs:
v2s=2kQqmR
Taking the square root gives:
vs=√2kQqmR
Step 6: Analyze the Relationship
From the equation vs=√2kQqmR, we can see that vs is proportional to the square root of q:
vs∝√q
Conclusion
Thus, the variation of escape velocity vs as a function of charge q is given by:
vs∝√q
We have a uniformly distributed negative charge Q within a sphere of radius R. A point charge q is located on the surface of this sphere. We need to determine how the escape velocity vs of the charge q varies with q.
The principle of conservation of mechanical energy states that the total mechanical energy at the initial point (when the charge is at the surface) must equal the total mechanical energy at the point of escape (where the potential energy is zero).
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
Initially, when the charge q is at the surface of the sphere, its kinetic energy is 12mv2s and the potential energy due to the charge Q is given by:
Ui=−kQqR
where k is Coulomb's constant. At the point of escape, the kinetic energy is 0 and the potential energy is also 0.
12mv2s−kQqR=0
Rearranging the equation gives us:
12mv2s=kQqR
Multiplying both sides by 2 leads to:
mv2s=2kQqR
Now, we can solve for the escape velocity vs:
v2s=2kQqmR
Taking the square root gives:
vs=√2kQqmR
From the equation vs=√2kQqmR, we can see that vs is proportional to the square root of q:
vs∝√q
Thus, the variation of escape velocity vs as a function of charge q is given by:
vs∝√q
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionA charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.
View Solution
Knowledge Check
A charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.
 Aq2B2qC4qDZero
Aq2B2qC4qDZeroA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.
 A−q,0B−q,qC0,0D0,q
A−q,0B−q,qC0,0D0,qIf charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
Ainversely proportional to (S+R)2Binversely proportional to R2.Cinversely proportional to S2.Ddirectly proportional to S2.
A charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionCharge Q is distributed on two concentric spheres of radius r and R resp. if charge density of both spheres is same then electric potential at centre will be
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
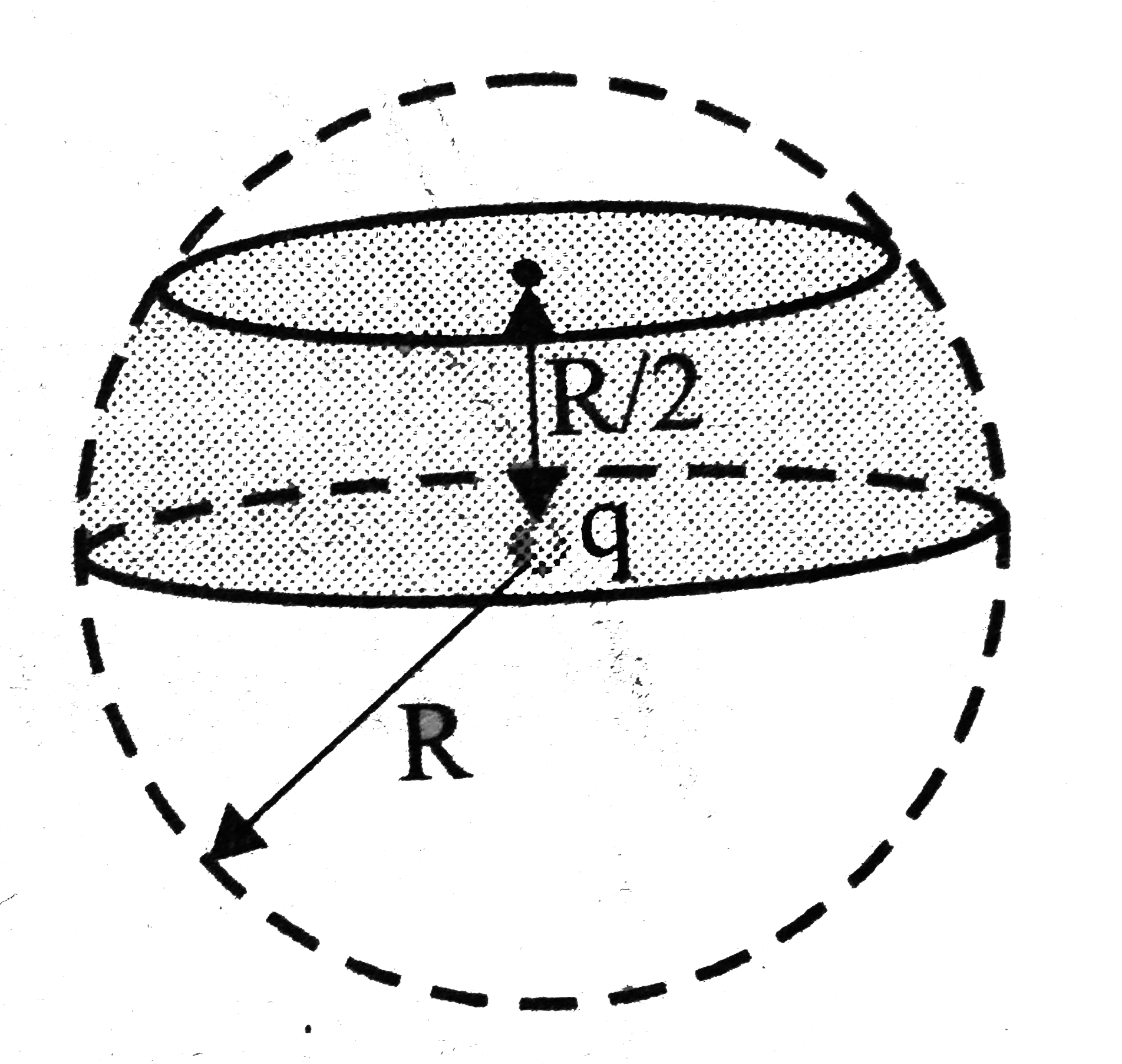
View SolutionIf charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
View SolutionA sphere is constructed around a positive point charge q. The work done in moving a unit positive charge on this sphere is numerically equal to
View Solution
