Four similar charges each of charge +q are placed at four corners of a square of side a. Find the value of integral −∫a/√2∞→E.→dr. (in volts) if value of integral −∫0a/√2→E.→dr=√2Kqa(whereK=14πε0)
4Kqa
3Kqa
3√2Kqa
4√2Kqa
The correct Answer is:C
To solve the problem, we need to find the value of the integral
−∫a√2−∞→E⋅d→r
given that
−∫0a√2→E⋅d→r=√2Kqa
where K=14πϵ0.
1. Understanding the Electric Field:
The electric field →E due to a point charge +q at a distance r is given by:
→E=Kqr2^r
where K=14πϵ0.
2. Setting Up the Integral:
We need to evaluate the integral from −∞ to a√2. We can break this into two parts:
−∫a√2−∞→E⋅d→r=−∫0−∞→E⋅d→r−∫a√20→E⋅d→r
3. Using the Given Value:
We know from the problem statement that:
−∫0a√2→E⋅d→r=√2Kqa
Therefore, we can substitute this into our expression:
−∫a√2−∞→E⋅d→r=−(−∫a√20→E⋅d→r+√2Kqa)
4. Combining the Integrals:
The integral from 0 to a√2 is the remaining part. Let's denote it as V0:
V0=−∫a√20→E⋅d→r
Thus, we have:
−∫a√2−∞→E⋅d→r=V0+√2Kqa
5. Finding the Value of the Integral:
Now, we need to find the total potential difference. The potential at infinity is zero, and at a√2 we have:
V=4Kq√2a
Therefore, we can express the total integral as:
V−0=4Kq√2a−√2Kqa
Simplifying gives:
V=3Kq√2a
6. Final Answer:
Thus, the value of the integral is:
−∫a√2−∞→E⋅d→r=3Kq√2a
The electric field →E due to a point charge +q at a distance r is given by:
→E=Kqr2^r
where K=14πϵ0.
We need to evaluate the integral from −∞ to a√2. We can break this into two parts:
−∫a√2−∞→E⋅d→r=−∫0−∞→E⋅d→r−∫a√20→E⋅d→r
We know from the problem statement that:
−∫0a√2→E⋅d→r=√2Kqa
Therefore, we can substitute this into our expression:
−∫a√2−∞→E⋅d→r=−(−∫a√20→E⋅d→r+√2Kqa)
The integral from 0 to a√2 is the remaining part. Let's denote it as V0:
V0=−∫a√20→E⋅d→r
Thus, we have:
−∫a√2−∞→E⋅d→r=V0+√2Kqa
Now, we need to find the total potential difference. The potential at infinity is zero, and at a√2 we have:
V=4Kq√2a
Therefore, we can express the total integral as:
V−0=4Kq√2a−√2Kqa
Simplifying gives:
V=3Kq√2a
Thus, the value of the integral is:
−∫a√2−∞→E⋅d→r=3Kq√2a
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Knowledge Check
If three point charges are placed at the three corners of a square of diagonals 2a as shown in figure. Then ∫AB→E.→dr will be -
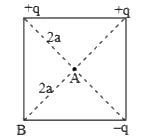 Aq4πε0aB−q8πε0aC−q4πε0aDq8πε0a
Aq4πε0aB−q8πε0aC−q4πε0aDq8πε0aThe value of the integral ∫100π0√1−cos2x dxis
A100√2B200√2C0D400√2Four charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the square will be (where k = 14πε0 )
A4kqaB4√2kqaC4kq√2aDkqa√2
The value of the integral
∫400π0√1−cos2xdx, is A√2. then find the value of A.
View SolutionIf the value of the integral ∫21ex2dx is α, then the value of ∫e4e√lnxdx is:
View SolutionThe value of the integral ∫log50ex√ex−1ex+3dx
View SolutionIf the value of the integral I=∫10dxx+√1−x2 is equal to πk, then the value of k is equal to
View SolutionThe value of the integral ∫π/20√cotx√cotx+√tanxdxis
View Solution
