The effective resistance between A and B in the figure 1.107 is 712Ω if each side of the cube has 1Ω resistances.The effective resistances between the same two points when the link AB is removed is

A
712Ω
B
512Ω
C
75Ω
D
57Ω
Text Solution
The correct Answer is:C
IF x is the effective resistance between A and B of the remaining cube, then
712=1×x1+x
Solving we get , x=75Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:EXAMINATION ARCHIVE WITH SOLUTIONS(JEE MAIN)
Explore 4 Videos
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:EXAMINATION ARCHIVE WITH SOLUTIONS(AIPMT)
Explore 2 Videos
- CURRENT ELECTRICITY Book:CHHAYA PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:EXAMINATION ARCHIVE WITH SOLUTIONS(WBCHSE)
Explore 18 Videos
- COMMUNICATION STSTEMBook:CHHAYA PUBLICATIONChapter:COMMUNICATION STSTEMExercise:CBSE SCANNER
Explore 28 Videos
- DIFFRACTION AND POLARISATION OF LIGHTBook:CHHAYA PUBLICATIONChapter:DIFFRACTION AND POLARISATION OF LIGHTExercise:CBSE SCANNER
Explore 27 Videos
Similar Questions
Knowledge Check
The effective resistance between A and B in the figure is 712Ω .If each side of the cube has 1 Ω resistance The effective resistance between the same two points, when the link AB is removed is
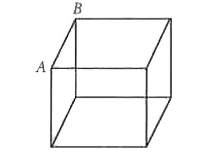 A712ΩB512ΩC75ΩD57Ω
A712ΩB512ΩC75ΩD57ΩThe effective resistance between the points A and B in the figure is
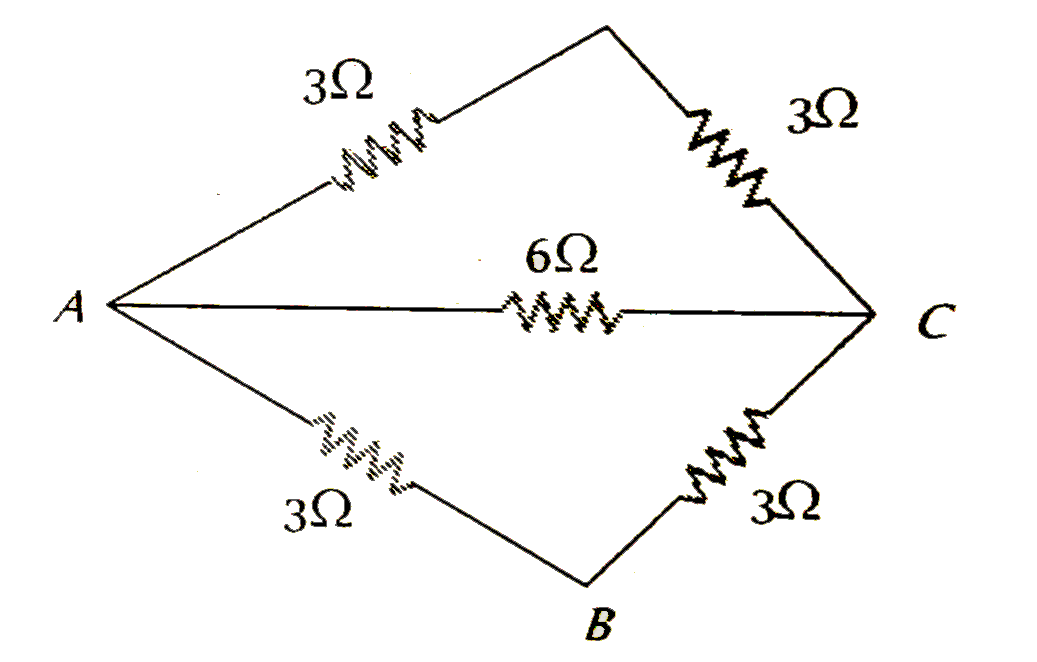 A5ΩB2ΩC3ΩD4Ω
A5ΩB2ΩC3ΩD4ΩIn the network shown in figure each resistance is 1Ω . The effective resistance between A and B is
 A43ΩB32ΩC7ΩD87Ω
A43ΩB32ΩC7ΩD87Ω
Find the effective resistance between the points A and B in figure.

View SolutionIn the net work each resistance is 2Ω. Find th effective resistance between AandB
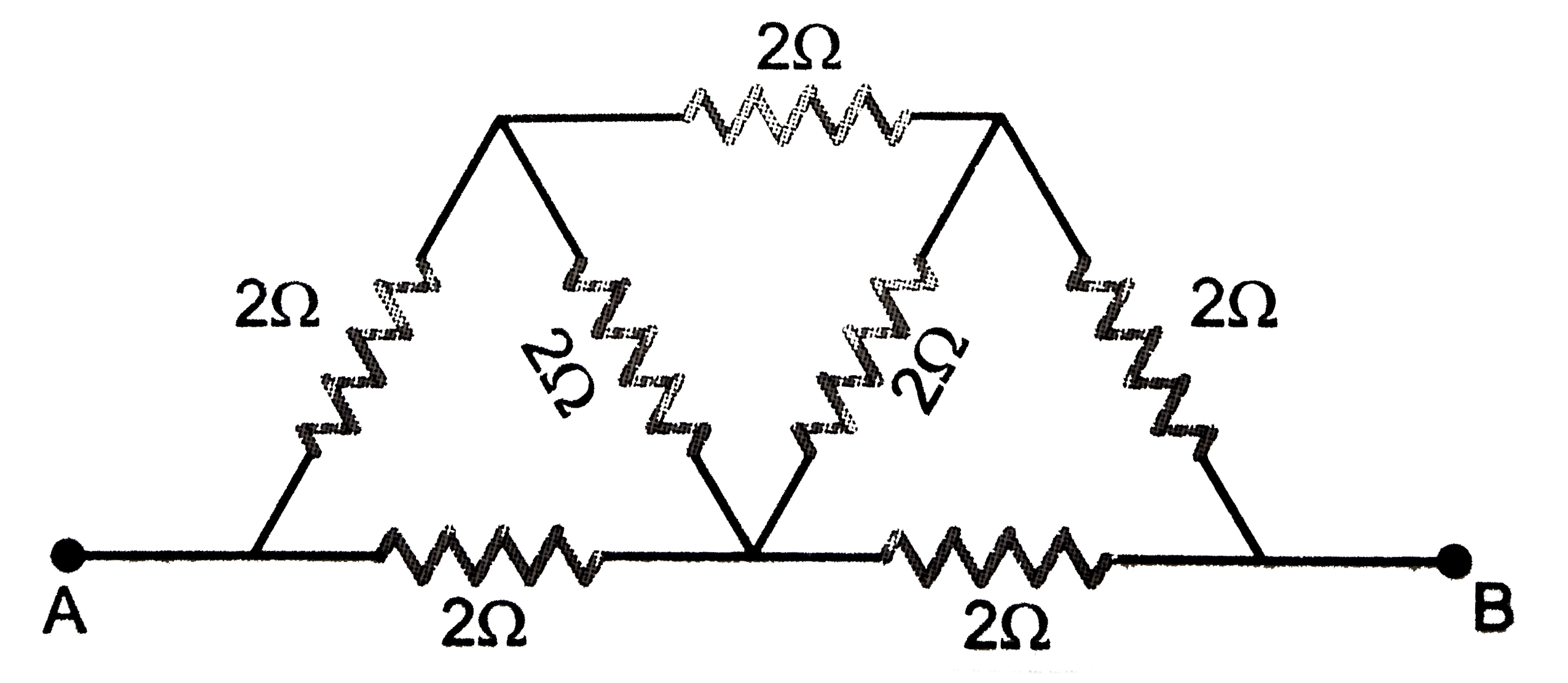
View SolutionIn the network shown in figure each resistance is 1Ω . The effective resistance between A and B is

View SolutionIn the network shown in figure each resistance is 1Ω. The effective resistance between A and B is

View SolutionShown in the figure is an infinite network of resistors each of resistance 1Ω . The effective resistance in between A and B is
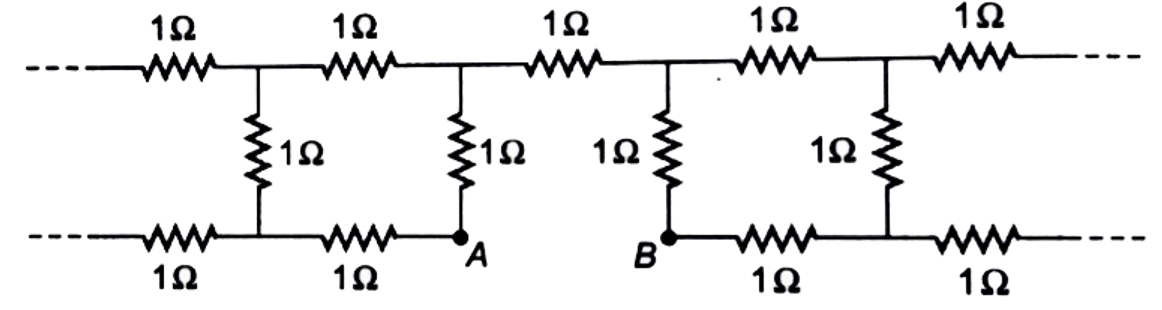
View Solution

