The angular velocities of three bodies in SHM are ω1,ω2,ω3 with their respective amplitudes as A1,A2,A3. If all three bodies have same mass and maximum velocity then
A1ω1=A2ω2=A3ω3
A1ω21=A2ω22=A3ω23
A21ω1=A22ω2=A23ω3
A21ω21=A22ω22=A2
The correct Answer is:A
Step by step video, text & image solution for The angular velocities of three bodies in SHM are omega_(1), omega_(2), omega_(3) with their respective amplitudes as A_(1),A_(2),A_(3). If all three bodies have same mass and maximum velocity then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Acceleration of simple Harmonic motion
Explore 21 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:Energy of simple Harmonic motion
Explore 34 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESS Chapter:SIMPLE HARMONIC MOTIONExercise:simple Harmonic Motion
Explore 21 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on motion of connected mass)
Explore 10 Videos
- SURFACE TENSIONBook:ERRORLESS Chapter:SURFACE TENSIONExercise:Exercise
Explore 214 Videos
Similar Questions
Knowledge Check
Three particles describes circular path of radii r1,r2andr3 with constant speed such that all the particles take same time to complete the revolution. If ω1,ω2,ω3 be the angular velocity v1,v2,v3 be linear velocities and a1,a2,a3 be linear acceleration than :
Aω1:ω2:ω3=1:1:1Bv1:v2:v3=r1:r2:r3Ca1:a2:a3=1:1:1Da1:a2:a3=r1:r2:r3If last three digits of the expression 17256 are
A1,A2 & A3 respectively then the value of expression 2A2+A3−44A1 equalsA0B−4C5D−7Two waves of nearly same amplitude , same frequency travelling with same velocity are superimposing to give phenomenon of interference . If a1 and a2 be their respectively amplitudes , ω be the frequency for both , v be the velocity for both and Δϕ is the phase difference between the two waves then ,
Athe resultant intensity varies periodically with time and distance.Bthe resulting intensity with IminImax=a1−a2(a1+a2)2 is obtained.Cboth the waves must have been travelling in the same direction and must be coherent.DIR=I1+I2+2√I1I2cos(Δϕ), where constructive interference is obtained for path difference that are odd multiple of 1/2λ and destructive interference is obtained for path difference that are even multiple of 1/2λ.
Let z1,z2,z3 be three complex numbers satisfying 1z1+1z2+1z3=0. Let zk=rk(cosαk+isinαk) and ωk=cos2αk+isin2αkzk for k=1,2,3. If ω1,ω2 and ω3 are the affixes of points A1,A2 and A3 respectively in the Argand plane, then ΔA1A2A3 has its
View SolutionIf two independent waves are y1=a1sinω1 and y2=a2sinω2t then
View SolutionThe number of all three element subsets of the set {a1,a2,a3......an} which contain a3 , is
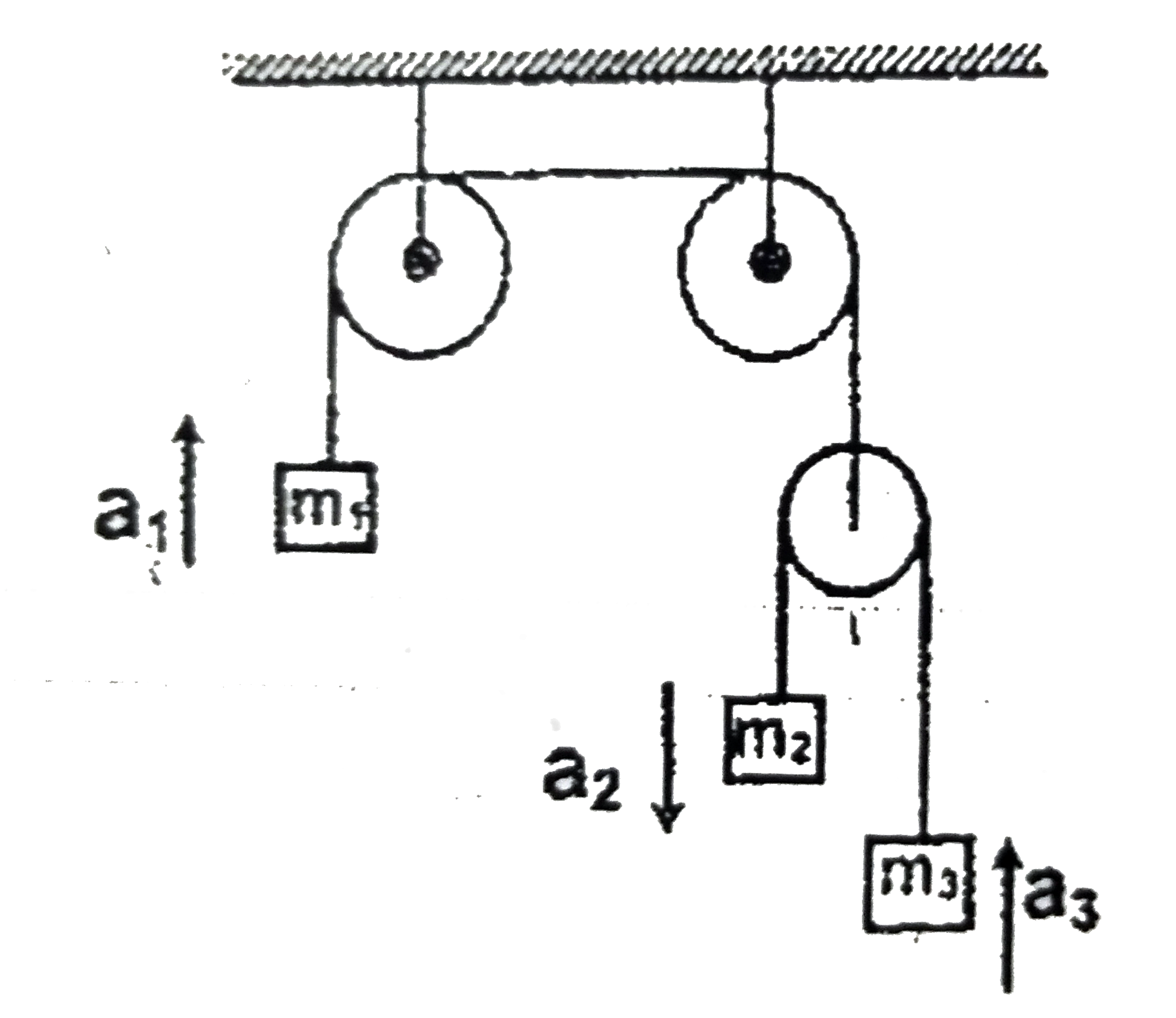
View SolutionIn the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
View SolutionThe maximum acceleration of a body moving is SHM is a0 and maximum velocity is v0. The amplitude is given by
View Solution

