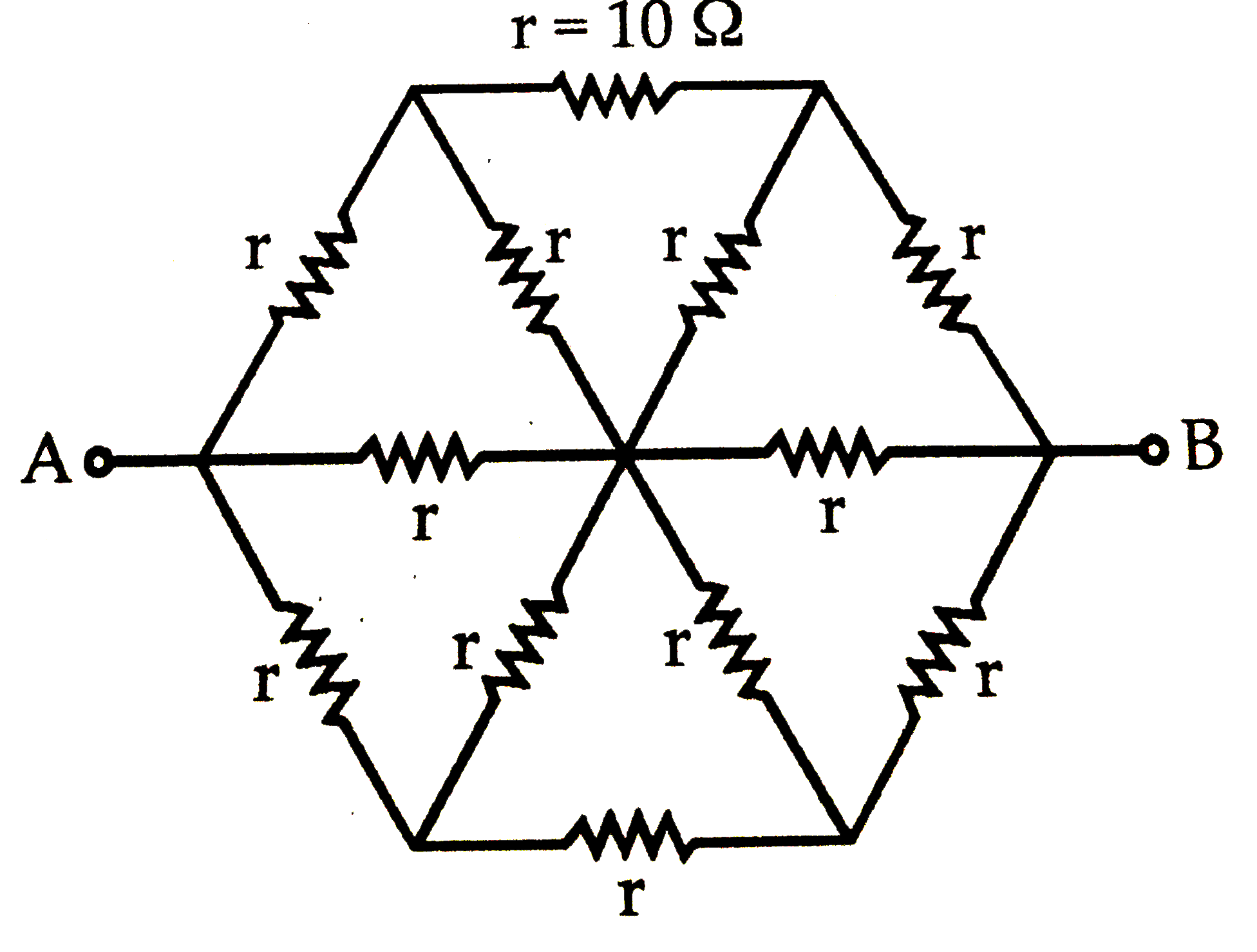
Three resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
4/3 ohm
3/4 ohm
3 ohm
6 ohm
The correct Answer is:A
To find the resistance between any two vertices of a triangular arrangement of three resistors, each of 2 ohms, we can follow these steps:
1. Understand the Configuration:
- We have three resistors (R1, R2, R3) each with a resistance of 2 ohms connected in a triangular shape. Let's label the vertices of the triangle as A, B, and C. The resistors are connected as follows: R1 between A and B, R2 between B and C, and R3 between C and A.
2. Identify the Points of Interest:
- We need to find the equivalent resistance between any two vertices. For this solution, let's calculate the resistance between points A and B.
3. Analyze the Circuit:
- When measuring the resistance between points A and B, the resistors R2 (between B and C) and R3 (between C and A) are in parallel. The resistor R1 (between A and B) is in series with the equivalent resistance of R2 and R3.
4. Calculate the Equivalent Resistance of R2 and R3:
- The formula for two resistors in parallel (R2 and R3) is given by:
Rparallel=R2⋅R3R2+R3
- Substituting the values:
Rparallel=2Ω⋅2Ω2Ω+2Ω=4Ω24Ω=1Ω
5. Combine with R1:
- Now, we add the equivalent resistance of the parallel combination (1 ohm) to R1 (2 ohms):
RAB=R1+Rparallel=2Ω+1Ω=3Ω
6. Final Result:
- The resistance between any two vertices (A and B) is 3 ohms.
- We have three resistors (R1, R2, R3) each with a resistance of 2 ohms connected in a triangular shape. Let's label the vertices of the triangle as A, B, and C. The resistors are connected as follows: R1 between A and B, R2 between B and C, and R3 between C and A.
- We need to find the equivalent resistance between any two vertices. For this solution, let's calculate the resistance between points A and B.
- When measuring the resistance between points A and B, the resistors R2 (between B and C) and R3 (between C and A) are in parallel. The resistor R1 (between A and B) is in series with the equivalent resistance of R2 and R3.
- The formula for two resistors in parallel (R2 and R3) is given by:
Rparallel=R2⋅R3R2+R3
- Substituting the values:
Rparallel=2Ω⋅2Ω2Ω+2Ω=4Ω24Ω=1Ω
- Now, we add the equivalent resistance of the parallel combination (1 ohm) to R1 (2 ohms):
RAB=R1+Rparallel=2Ω+1Ω=3Ω
- The resistance between any two vertices (A and B) is 3 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Kirchhoff s Law, cells
8 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Different Measuring Instruments
1 Video
- COMMUNICATION SYSTEMBOOK - ERRORLESS CHAPTER - COMMUNICATION SYSTEMEXERCISE - S E T
14 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET
20 Videos
Similar Questions
Knowledge Check
Three resistors, each of 2Ω are connected together in a triangular shape. The resistance offered between any two vertices will be
A3ΩB6ΩC43ΩD34ΩThree resistance each of 4Ω are connected to form a triangle. The resistance between any two terminals is
A12ΩB2ΩC6ΩD83ΩThree resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
A3ΩB4ΩC6ΩD43Ω
Three resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
View Solution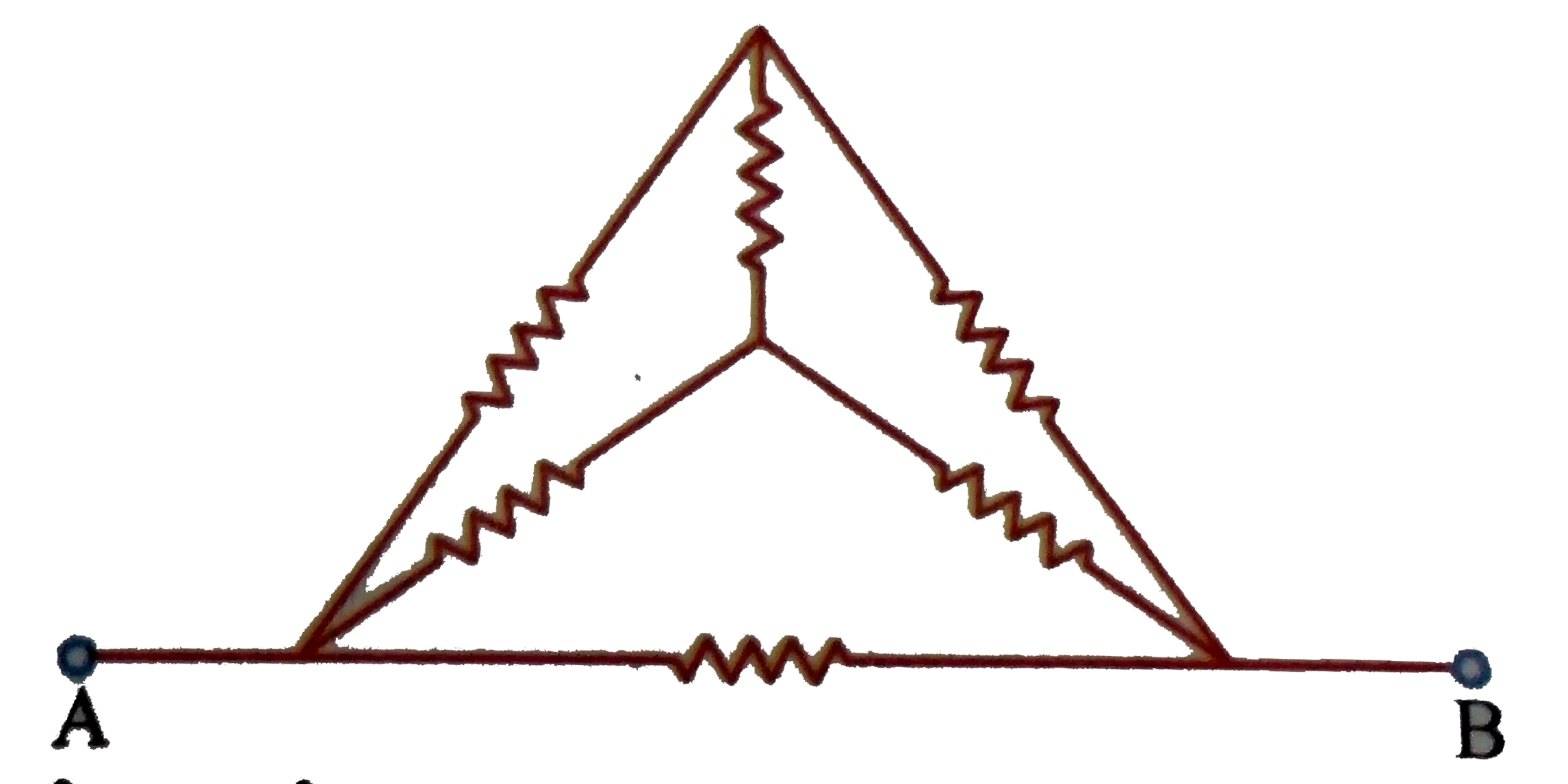
Six resistors of each 2 ohm are connected as shown in the figure. The resultant resistance between A and B is.
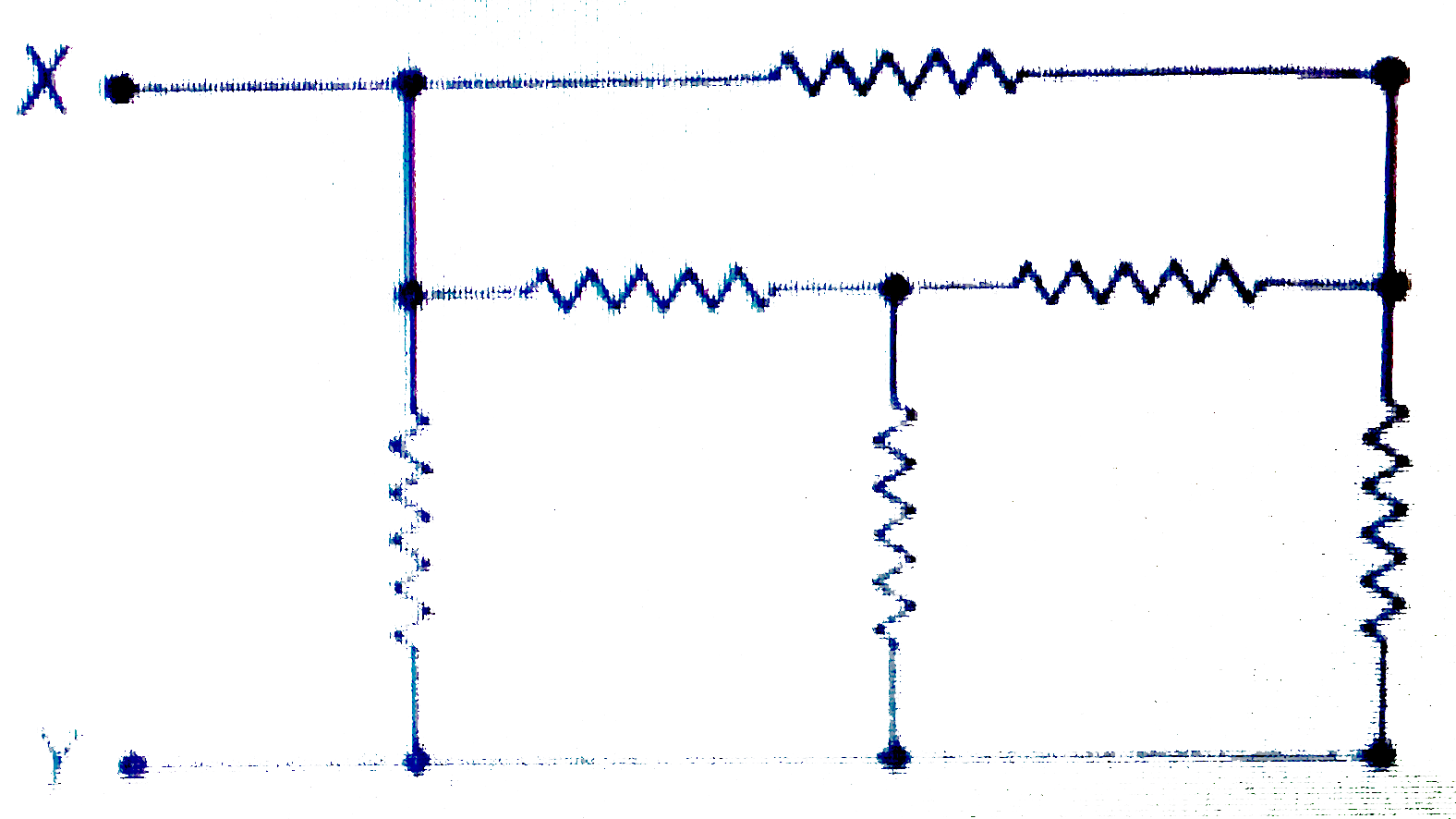
View SolutionSix resistors each of 10 ohm are connected shown. The equivalent resistance between points X and Y is
View SolutionThree resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
View SolutionThree resistances 4Ω each of are connected in the form of an equilateral triangle. The effective resistance between two corners is
View Solution