A small cork block of mass m=1kg having charge q=−1C placed on a rough horizontal surface and is connected to a vertical wall through an unstretched non conducting light spring of spring consant k=9N/m as shown in the figure. If a horizontal constant electric field E=10N/C is switched on then the maximum compression in the spring is xm. Find the value of x. (Take g=10m/s2,μ=0.1) 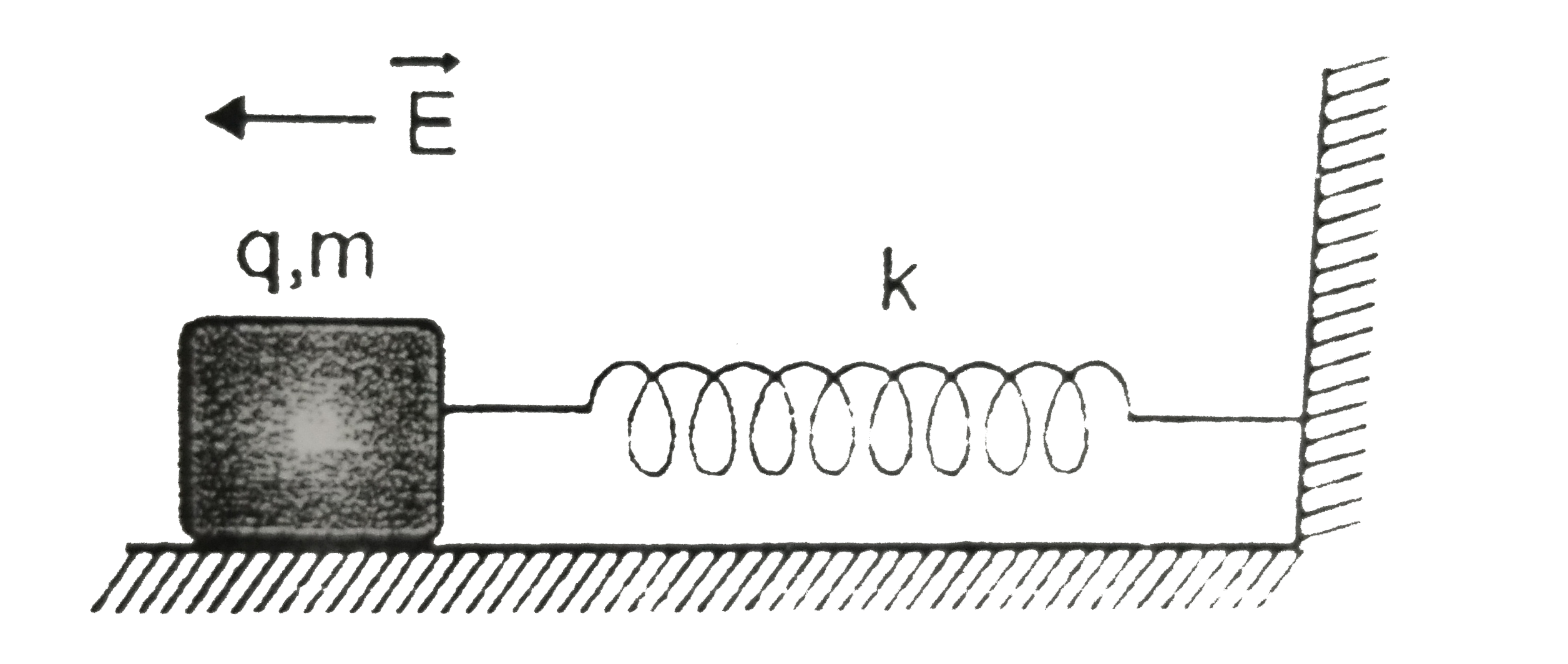
The correct Answer is:2
Applying work kinetic energy theorem
|q|Ex−12kx2−μmgx=0
Putting the values we will get x=2m 
Similar Questions
A block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
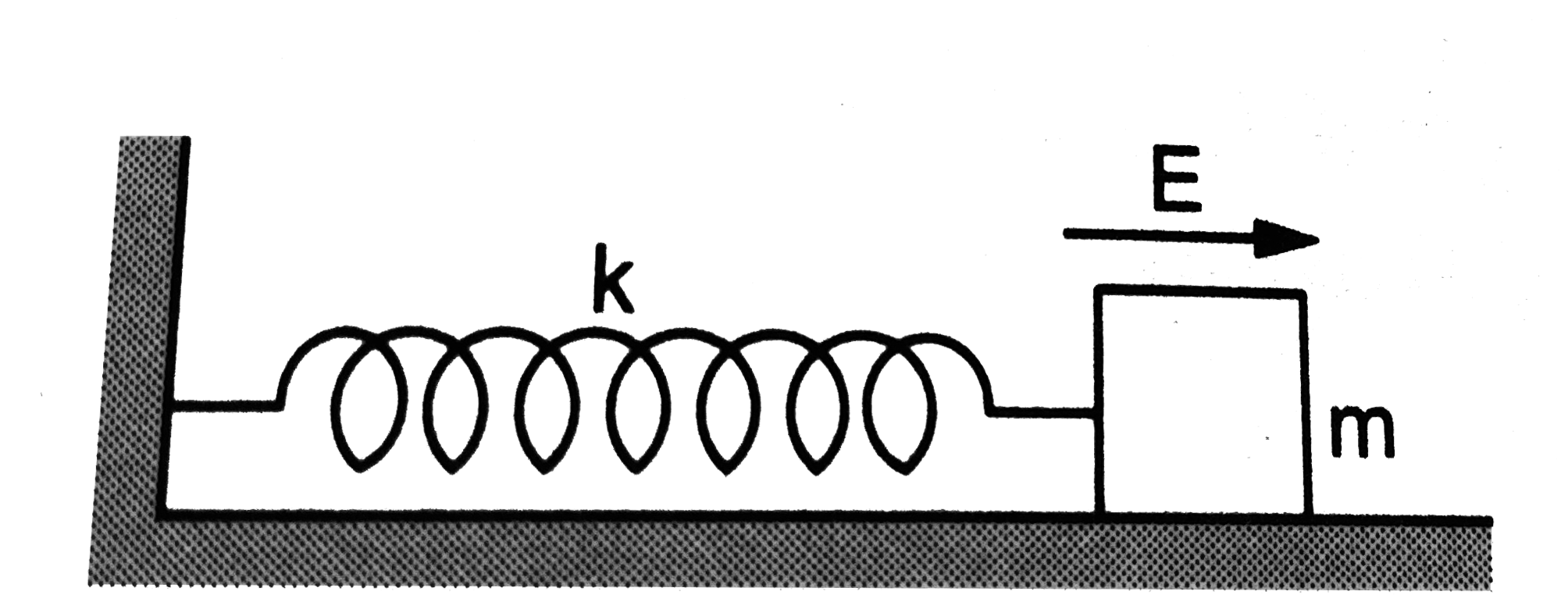
View SolutionTwo identical blocks each of mass M=9kg are placed on a rough horizontal surface of frictional coefficient μ=0.1. The two blocks are joined by a light spring and block B is in contact with a vertical fixed wall as shown in figure. A bullet of mass m=1kg and v0=10m/s hits block A and gets embedded in it. Find the maximum compression of spring. (Spring constant =240N/m,g=10m/s2)

View Solution
Knowledge Check
A block of mass m containing a net negative chage −q is placed on a froctionless horizontal tabe and is connected to a wall through an unstreached spring of spring constant k. If the horizontal electric field E parallel to spring is switched on , then the maximum compression of the spring is
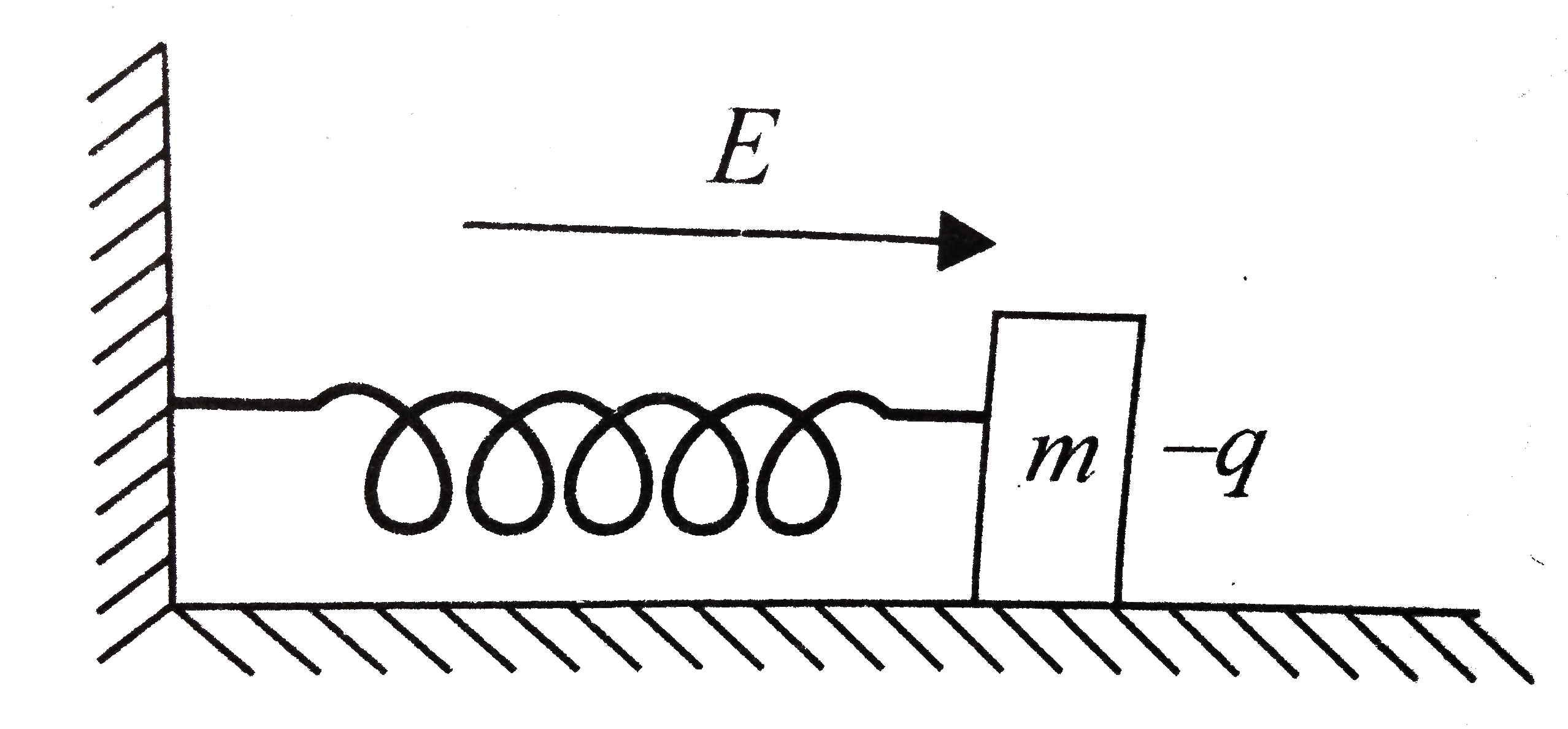 A√qE/kB2qE/kCqE/kDzero
A√qE/kB2qE/kCqE/kDzeroA particular of mass m and having a charge q is placed on a smooth horizontal table and is connected to walls through unstressed springs of constant k (shown in figure). A horizontal electric field E parallel to spring is switched On. The maximum speed of the particle
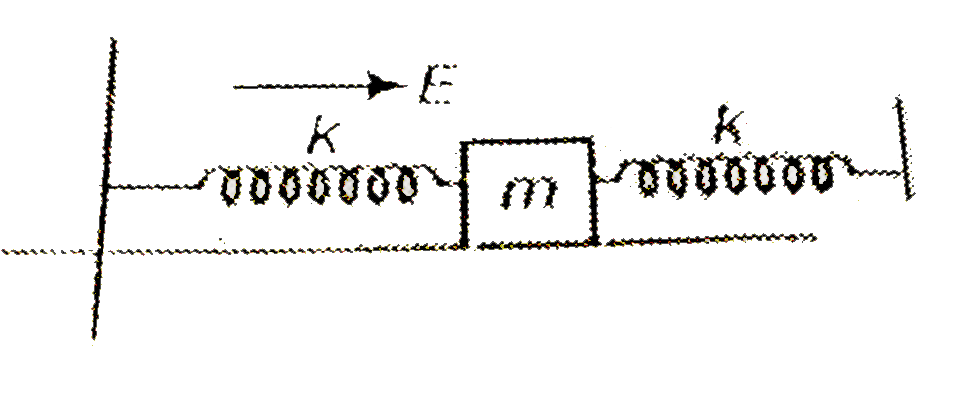 AqE√(2mk)BqEmkCqEmDnone of these
AqE√(2mk)BqEmkCqEmDnone of theseA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
Two blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
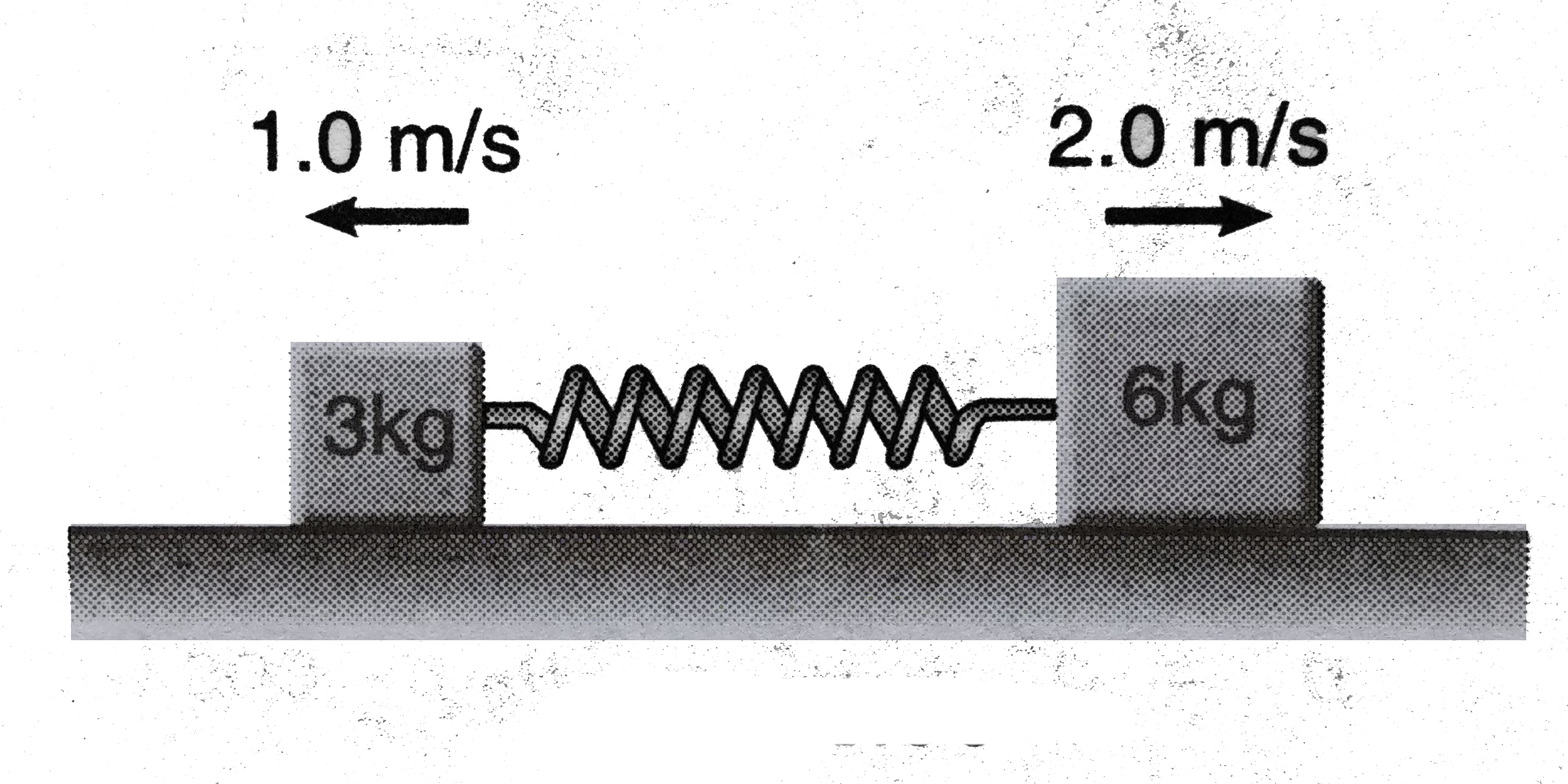
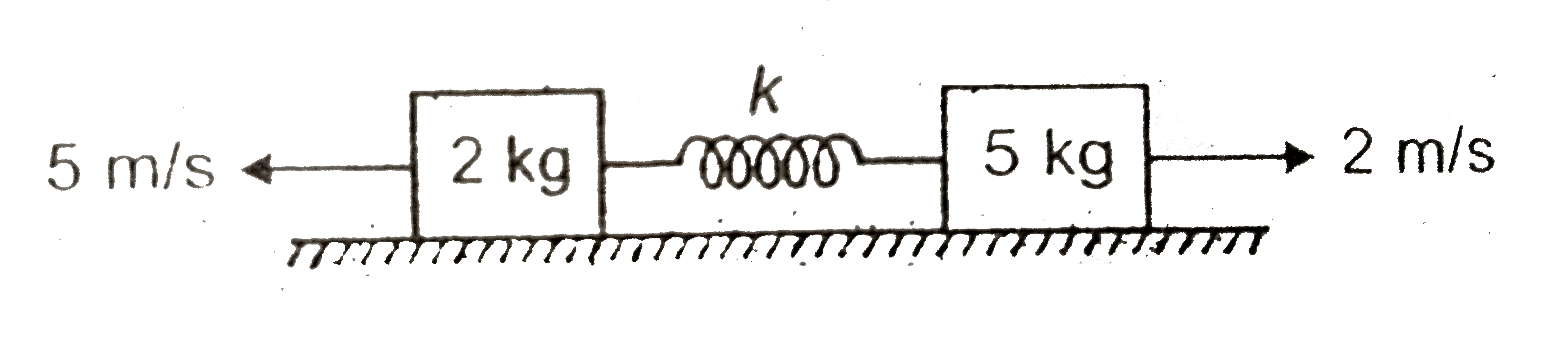
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
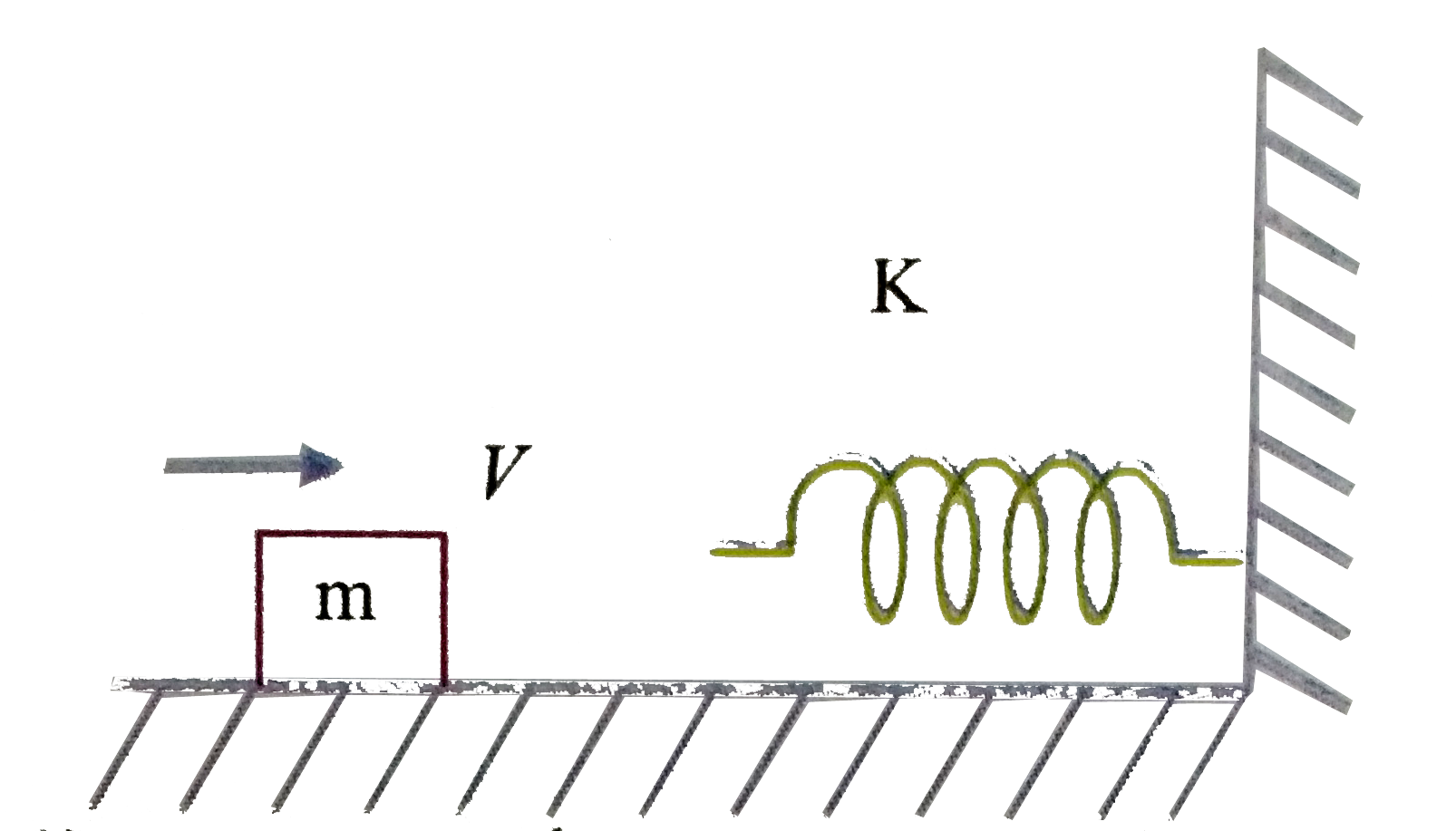
View SolutionA point mass m and charge q is connected with massless spring of natural length L. Initially spring is in its natural length. If a horizontal uniform electric field E is switched on as shown in figure, then the maximum separation between the point mass and the wall is: (Assume all surface are frictionless)

View SolutionA block of mass m=25kg on a smooth horizontal surface with a velocity →v=3ms−1 meets the spring of spring constant k=100N/m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
 .
.
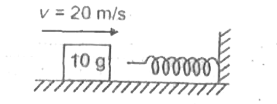
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View Solution

