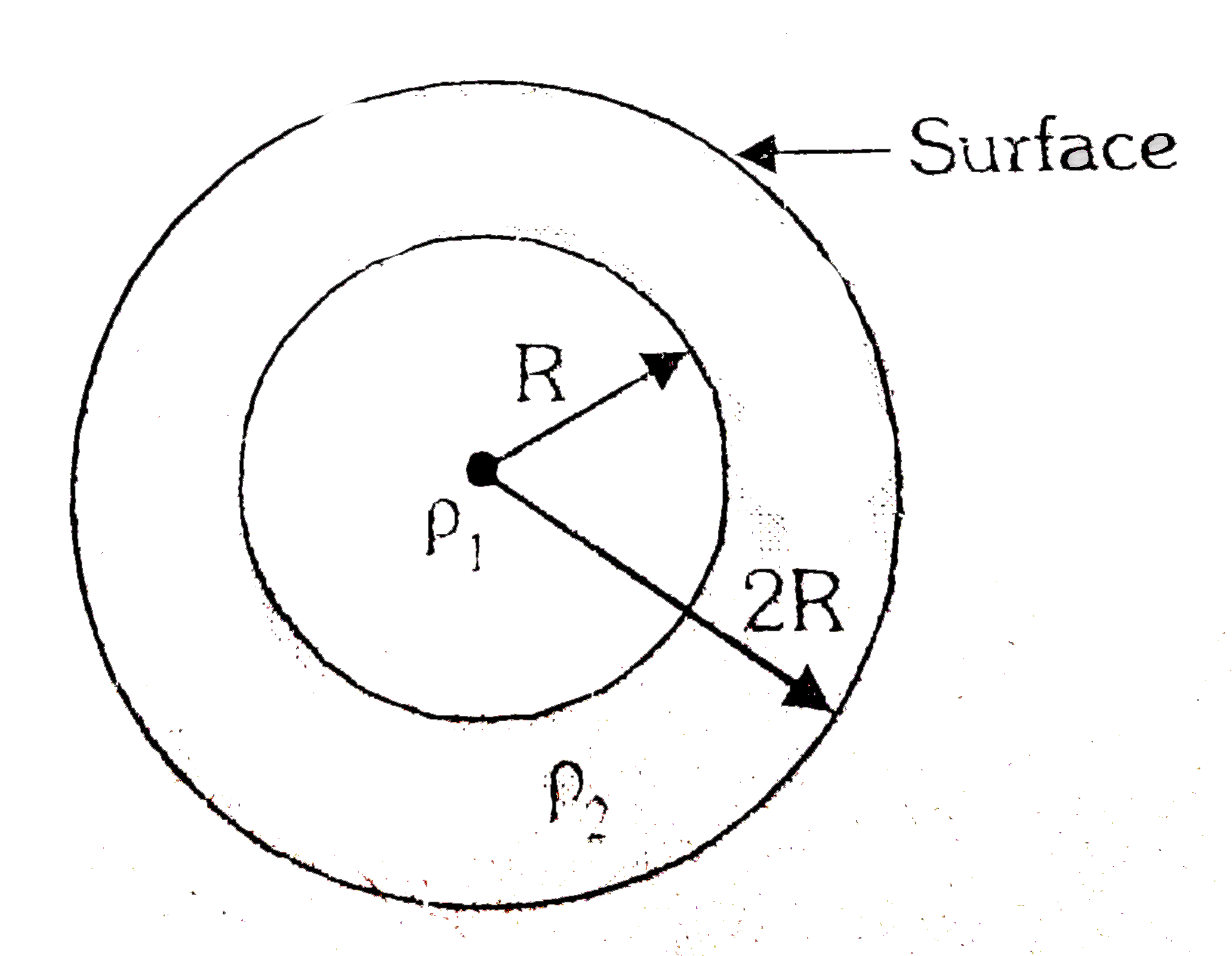
A planet is made of two materials of density ρ1 and ρ2 as shown in figure. The acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of ρ1ρ2 is x3. Find the value of x. 
The correct Answer is:7
GM(2R)2=GM′R2
M4=M′
43πR3ρ1+43π(8R3−R3)ρ2=4(43.πR3.ρ1)
ρ1+7ρ2=4ρ1
ρ1ρ2=72
Similar Questions
A planet is made of two materials of density p1 and p2 as shown in figure. Th acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of p1p2 is ab. Find value of ab+186 (a and b are lowest possible integers)
View SolutionThe density of the core of a planet is x and that of outer shell is y. The radii of the core and that of the planet are R and 2R. The acceleration due to gravity at the surface of planet is same as at a depth R. The ratio of x and y is n/3. Find the value of n.
View Solution
Knowledge Check
Two planets are of the same material but their radii are in the ratio 2:1. Then ratio of accelerations due to gravity on those two planets is
A2:1B1:2C4:1D1:4Two planets have radii r1and2r1 and densities are ρ1and4ρ1 respectively. The ratio of their acceleration due to gravities is
A1:8B8:1C4:1D1:4The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
AρRBρR−1Cρ−1R−2DρR2
The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the radio of ρ1ρ2

View SolutionTwo planets of radii r1 and r2 are made from the same material. The ratio of the acceleration of gravity g1/g2 at the surfaces of the planets is
View SolutionThe density of the core of planet is ρ1 and that of the outer shell is ρ2. The radius of the core that of the planet are R and 2R respectively. Gravitastional intensity at the surface of the planet is same as at a depth R. Find the ratio ρ1ρ2 , assuming them to be uniform independently.

View SolutionA composite rod made up of two conductors of resistivity ρ1 and ρ2 is shown in the figure. If face A and B are connected to a battery, find the resistance of the rod.
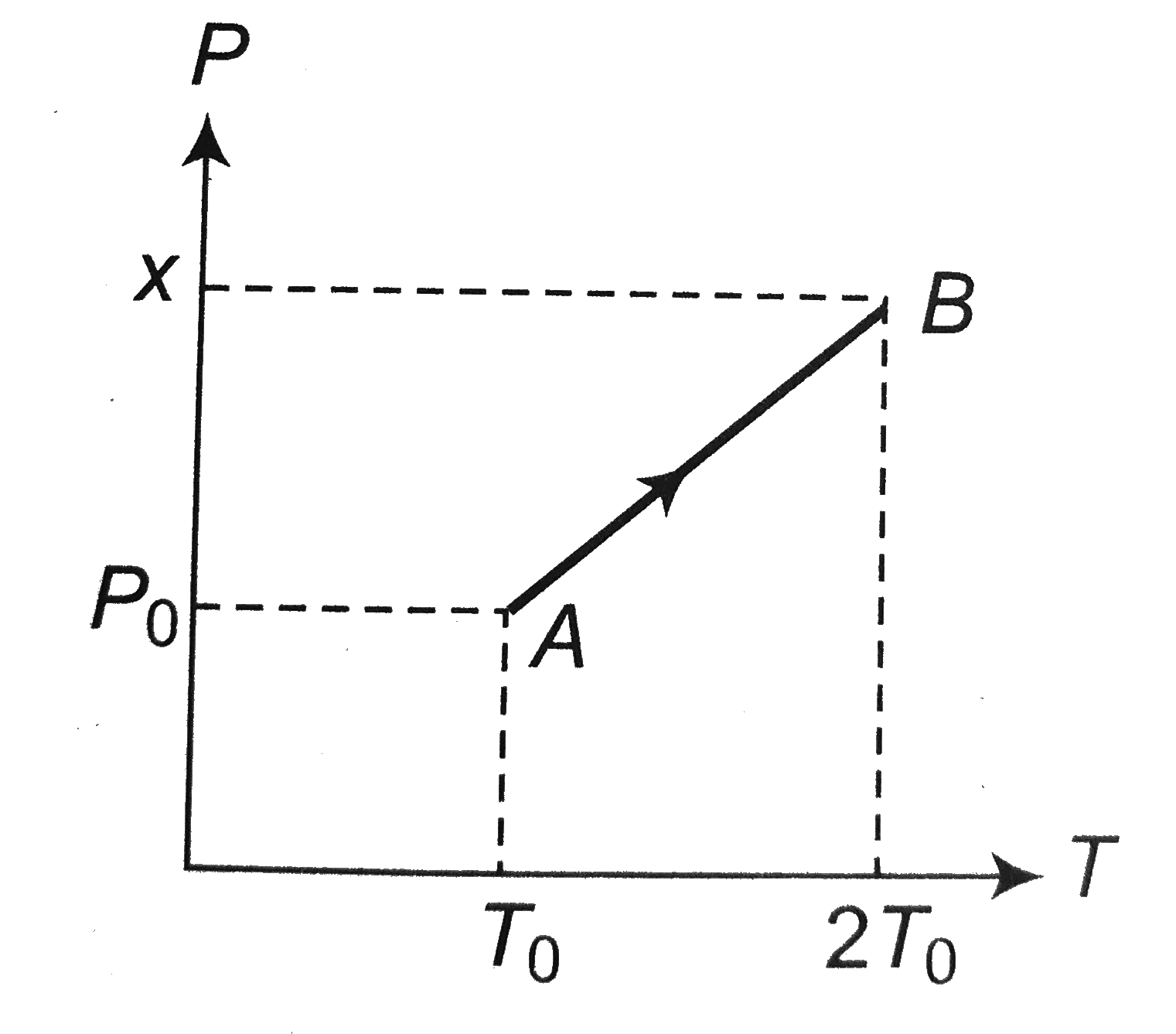
View SolutionThe densities at points A and B are ρ0 and 3ρ02. Find the value of x on P-axis.
View Solution