Sixteen players P(1),P(2),P(3)….., P(16) play in tournament. If they g

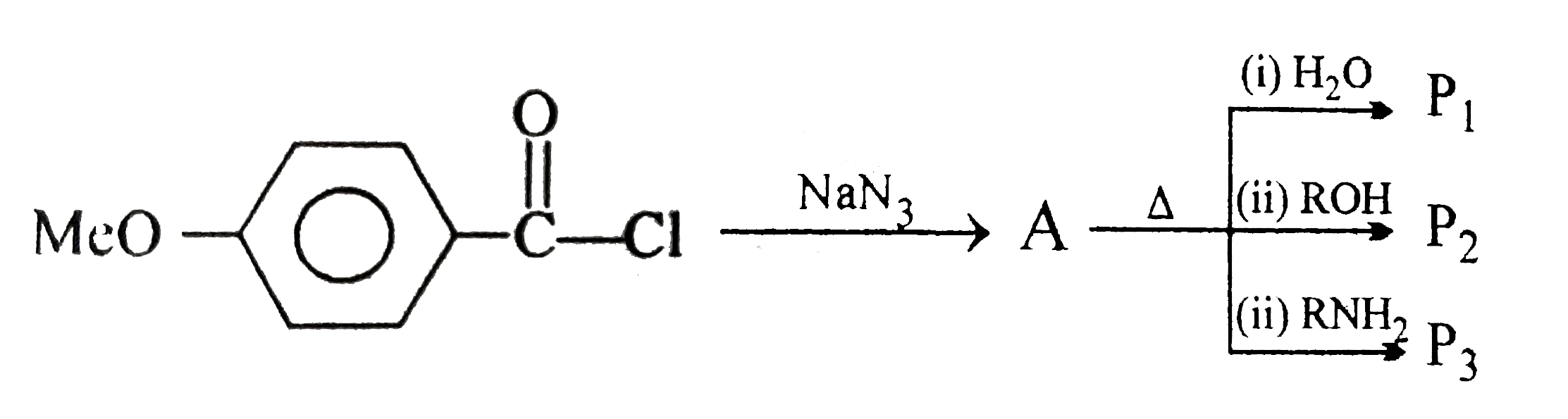
$P_{1}, P_{2}, P_{3}, a r e :$
A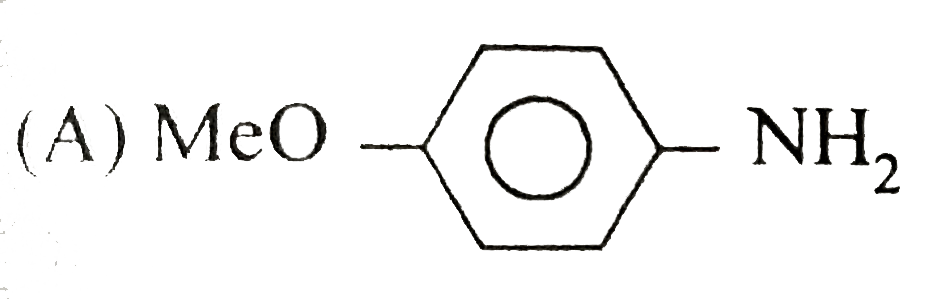
B
C
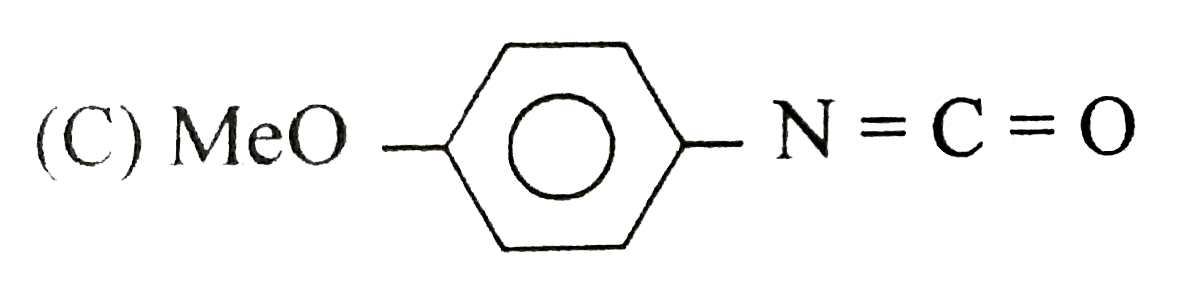D
Sixteen players $S_{1}$ , $S_{2}$ , $S_{3}$ ,…, $S_{16}$ play in a tournament. Number of ways in which they can be grouped into eight pairs so that $S_{1}$ and $S_{2}$ are in different groups, is equal to
A $\frac{(14)!}{2^{6} \cdot 6!}$
B $\frac{(15)!}{2^{7} \cdot 7!}$
C $\frac{(14)!}{2^{7} \cdot 6!}$
D $\frac{(14)!}{2^{6} \cdot 7!}$
16 players $P_{1}, P_{2}, P_{3}, \dots . P_{16}$ take part in a tennis tournament. Lower suffix player is better than any higher suffix player. These players are to be divided into 4 groups each comprising of 4 players and the best from each group is selected to semifinals.
Q. Number of ways in which they can be divided into 4 equal groups if the players $P_{1}, P_{2}, P_{3}$ and $P_{4}$ are in different groups, is:
A $\frac{(11)!}{216}$
B $\frac{(12)!}{{(3!)}^{4}}$
C $\frac{(12)!}{{(3!)}^{4} (4!)}$
D $\frac{(11)!}{{(3!)}^{4}}$

Sixteen players $P_{1}, P_{2}, P_{3} \dots . ., P_{16}$ play in tournament. If they grouped into eight pair then the probability that $P_{4}$ and $P_{9}$ are in different groups, is equal to