A particle is moving in x−y plane with y=x2 and Vx=4−2t. The displacement versus time graph of the particle would be
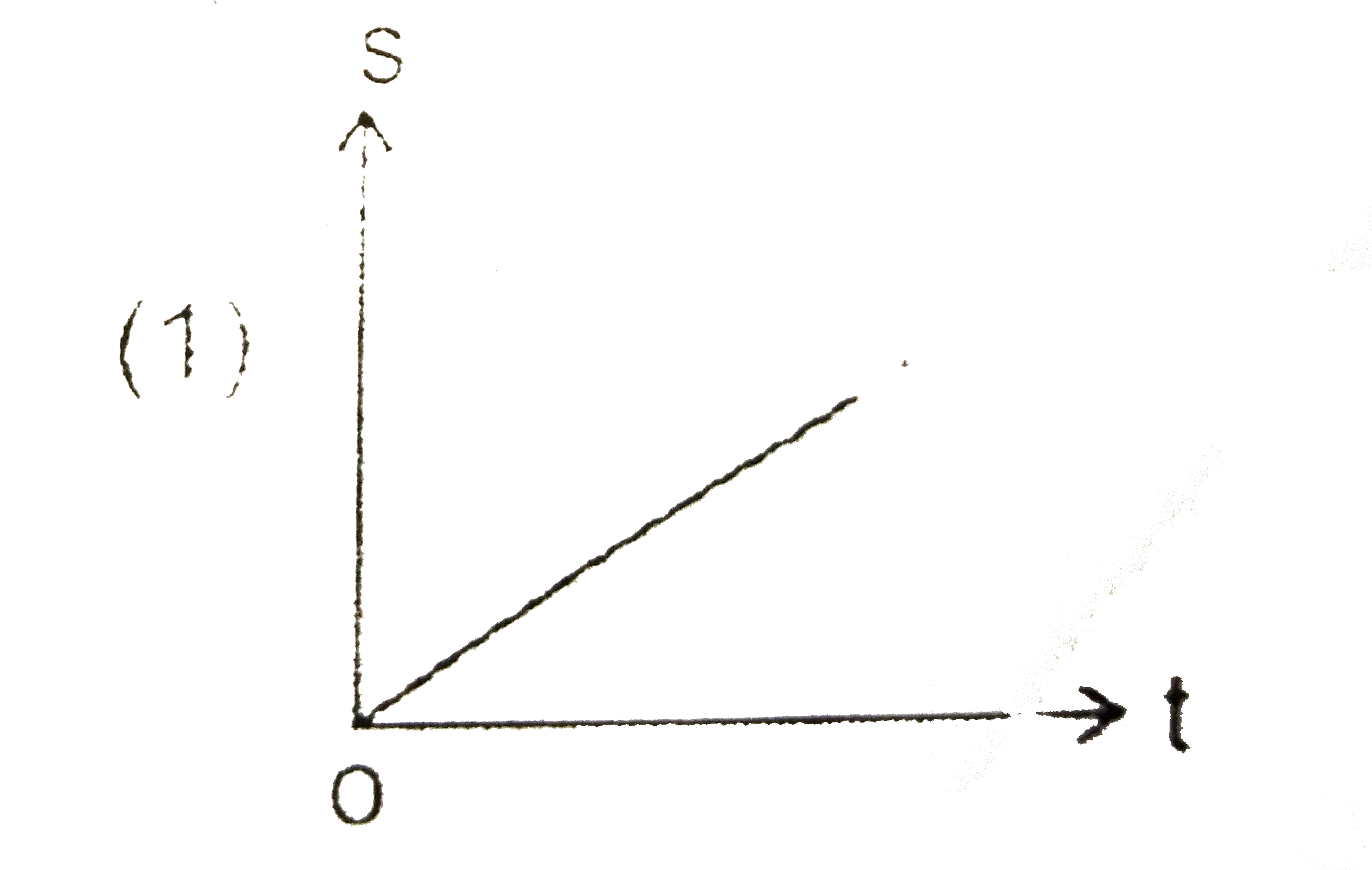
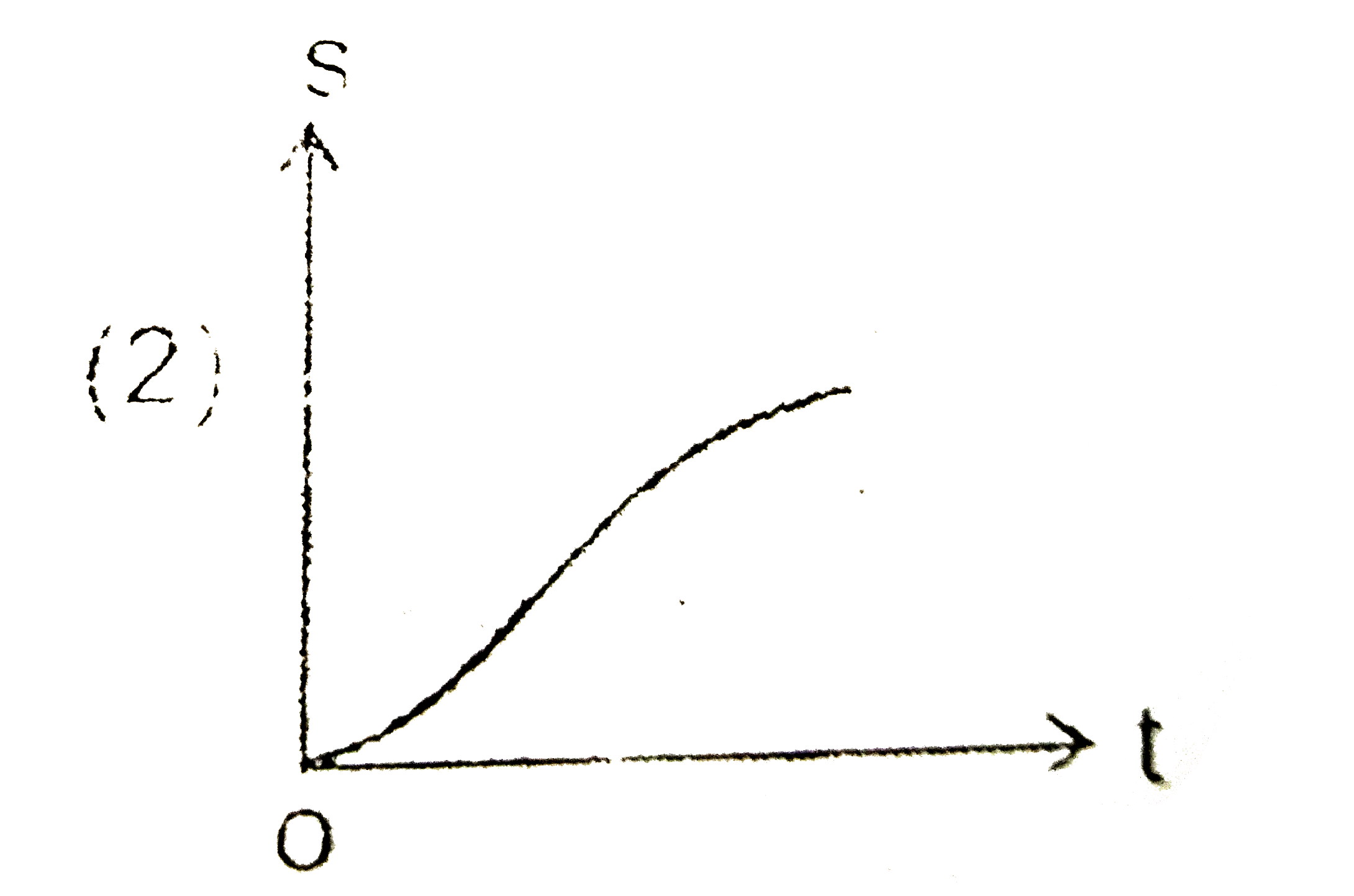
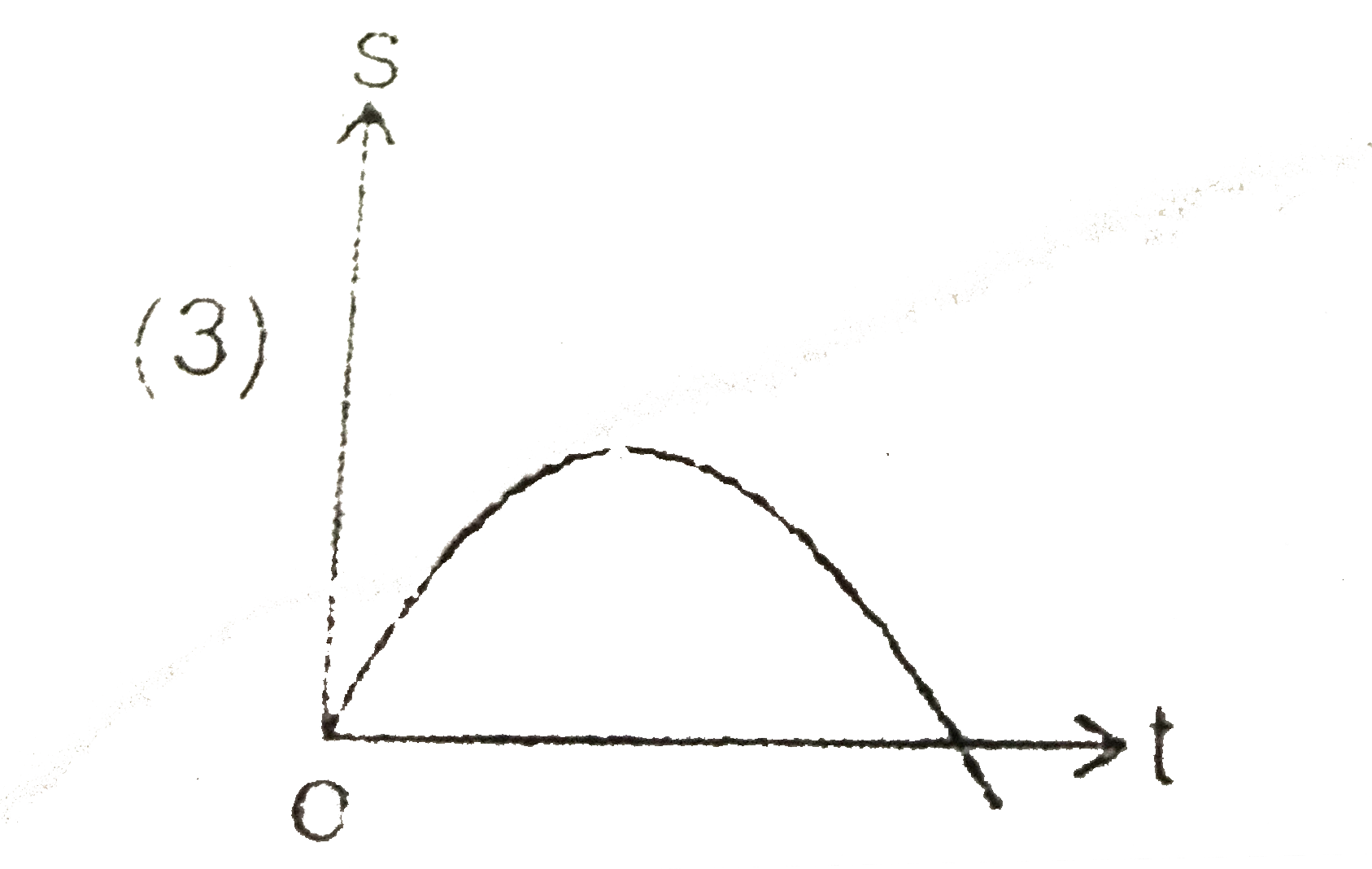
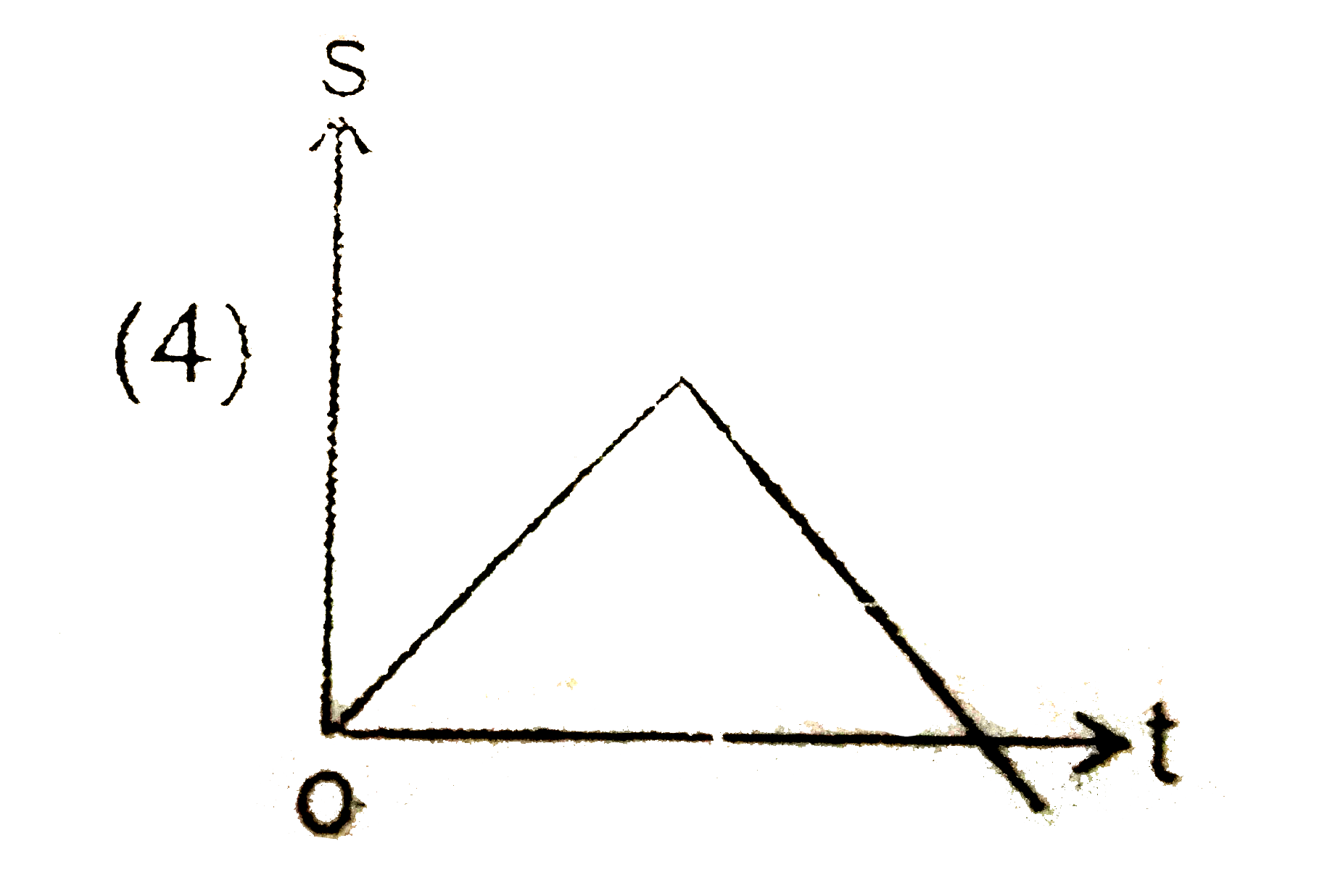
The correct Answer is:C
To solve the problem, we need to find the displacement versus time graph for a particle moving in the x-y plane with the given conditions. Let's break it down step by step.
Step 1: Understand the Motion in the x-y Plane
The particle's motion is described by the equation y=x2. This indicates that the y-coordinate is always half of the x-coordinate.
Step 2: Analyze the Velocity in the x-direction
We are given the velocity in the x-direction as:
Vx=4−2t
This represents how the x-component of the velocity changes with time.
Step 3: Relate Velocity to Displacement
The velocity in the x-direction can be expressed as:
Vx=dxdt
Thus, we can write:
dxdt=4−2t
Step 4: Integrate to Find Displacement in the x-direction
To find the displacement x(t), we integrate the equation:
dx=(4−2t)dt
Integrating both sides from t=0 to t and x=0 to x:
∫dx=∫(4−2t)dt
This gives:
x=4t−t2+C
Assuming the initial condition x(0)=0, we find C=0. Thus:
x(t)=4t−t2
Step 5: Find the Corresponding y-coordinate
Using the relationship y=x2:
y(t)=12(4t−t2)=2t−t22
Step 6: Find the Displacement
The total displacement D from the origin can be calculated using the Pythagorean theorem:
D=√x2+y2
Substituting x(t) and y(t):
D=√(4t−t2)2+(2t−t22)2
Step 7: Simplify the Expression
Calculating D:
1. Calculate (4t−t2)2=16t2−8t3+t4
2. Calculate (2t−t22)2=4t2−2t3+t44
Now combine:
D2=(16t2−8t3+t4)+(4t2−2t3+t44)
D2=20t2−10t3+5t44
Thus, the displacement D is:
D=√20t2−10t3+5t44
Step 8: Analyze the Displacement vs Time Graph
To understand the displacement versus time graph, we observe how D changes with t. The leading term is 20t2, which indicates that the displacement will initially increase quadratically with time, but the presence of the cubic and quartic terms will affect the curvature of the graph as t increases.
Summary of the Solution
The displacement versus time graph will start at the origin and initially rise, following a quadratic trend, but will eventually curve due to the influence of the cubic and quartic terms.
The particle's motion is described by the equation y=x2. This indicates that the y-coordinate is always half of the x-coordinate.
We are given the velocity in the x-direction as:
Vx=4−2t
This represents how the x-component of the velocity changes with time.
The velocity in the x-direction can be expressed as:
Vx=dxdt
Thus, we can write:
dxdt=4−2t
To find the displacement x(t), we integrate the equation:
dx=(4−2t)dt
Integrating both sides from t=0 to t and x=0 to x:
∫dx=∫(4−2t)dt
This gives:
x=4t−t2+C
Assuming the initial condition x(0)=0, we find C=0. Thus:
x(t)=4t−t2
Using the relationship y=x2:
y(t)=12(4t−t2)=2t−t22
The total displacement D from the origin can be calculated using the Pythagorean theorem:
D=√x2+y2
Substituting x(t) and y(t):
D=√(4t−t2)2+(2t−t22)2
Calculating D:
1. Calculate (4t−t2)2=16t2−8t3+t4
2. Calculate (2t−t22)2=4t2−2t3+t44
D2=(16t2−8t3+t4)+(4t2−2t3+t44)
D2=20t2−10t3+5t44
Thus, the displacement D is:
D=√20t2−10t3+5t44
To understand the displacement versus time graph, we observe how D changes with t. The leading term is 20t2, which indicates that the displacement will initially increase quadratically with time, but the presence of the cubic and quartic terms will affect the curvature of the graph as t increases.
The displacement versus time graph will start at the origin and initially rise, following a quadratic trend, but will eventually curve due to the influence of the cubic and quartic terms.
Similar Questions
Knowledge Check
A particle id moving in xy - plane with y=x/2andvx=4−2t. Choose the correct options.
AInitial velocities in x and y directions are negative.BInitial velocities in x and y directions are positive.CMotion is first retarded, then accelerated.DMotion is first accelerated, then retarded.Figure show the displacement - time graph of a particle moving on the x-axis
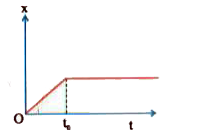 Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.The position of a particle moving in x-y plane changes with time t given by →x=3t2ˆi+9tˆj. The acceleration of particle would be
A2 m/s^2B3 m/s^2C4 m/s^2D6 m/s^2
A particle moves in y plane according to the law x=4sin6t and y=4(1-cot6t) .The distance traversed by the particle in 4 seconds (in meter) s (x and y are in
View SolutionA particle moves in x−y plane according to the law x=4sin6tandy=4(1−cos6t). The distance traversed by the particle in 4 second is (x&y are in meters)
View SolutionA particle moves in x-y plane according to equations x=4t2+5t and 6y=5t The acceleration of the particle must be
View SolutionThe acceleration versus time graph of a particle moving in a straight line is show in figure. The velocity-time graph of the particle would be
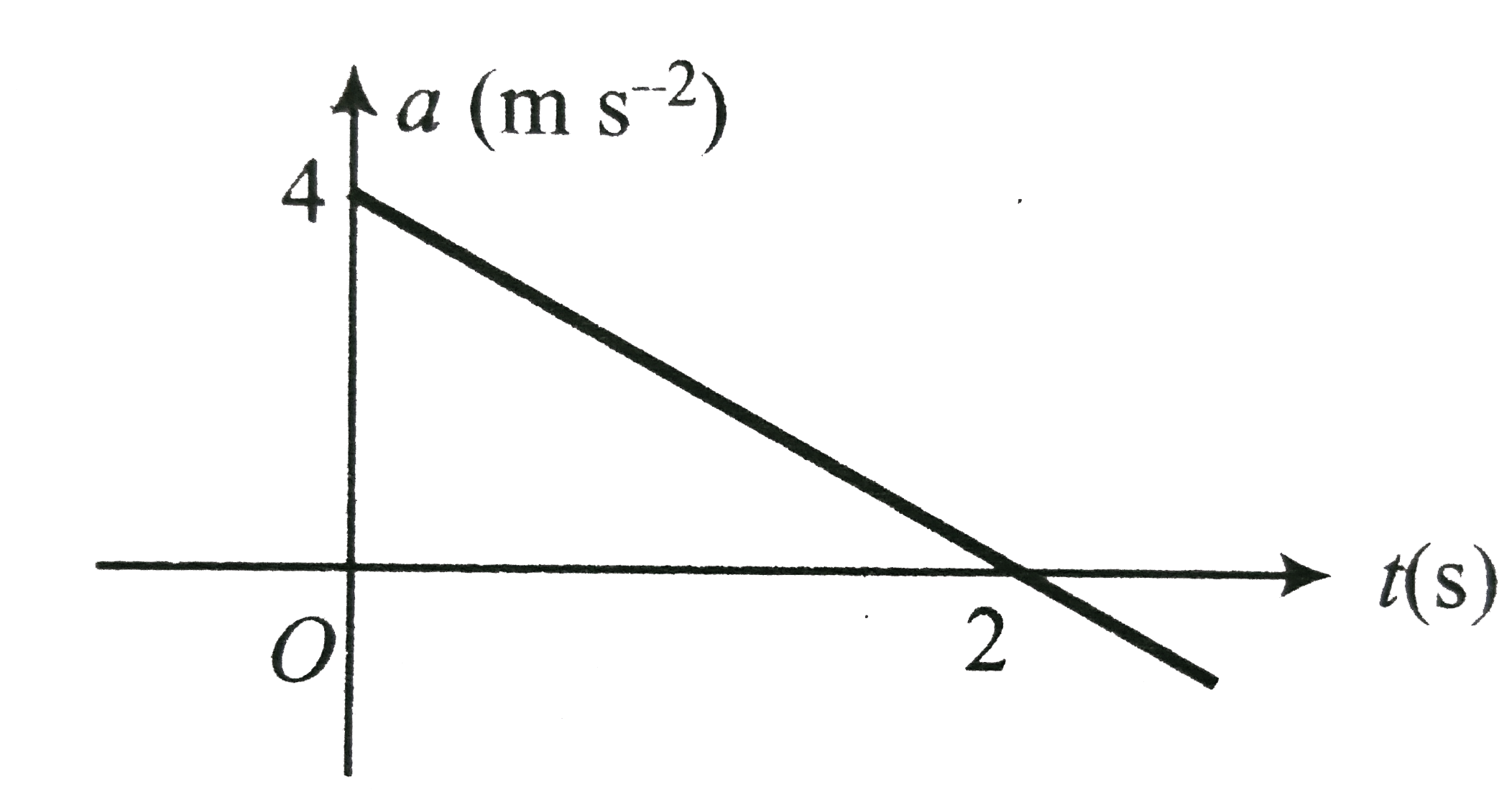 .
.
View SolutionThe co-ordinates of a particle moving in xy-plane vary with time as x=at2,y=bt. The locus of the particle is :
View Solution

