x and y displacements of a particle are given as x(t)=−asinωt and y(t)=asin2ωt. Its trajectory will look like.
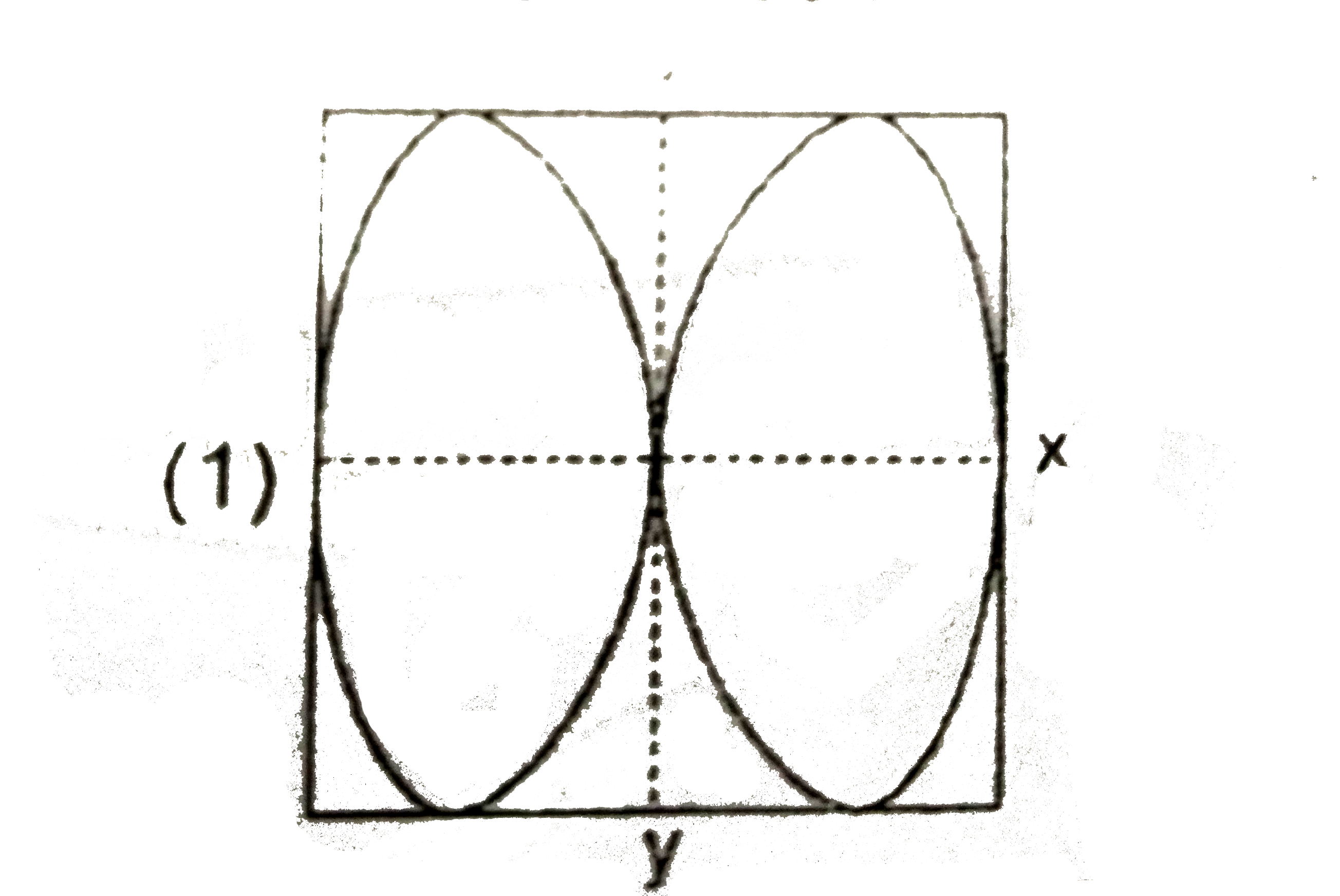
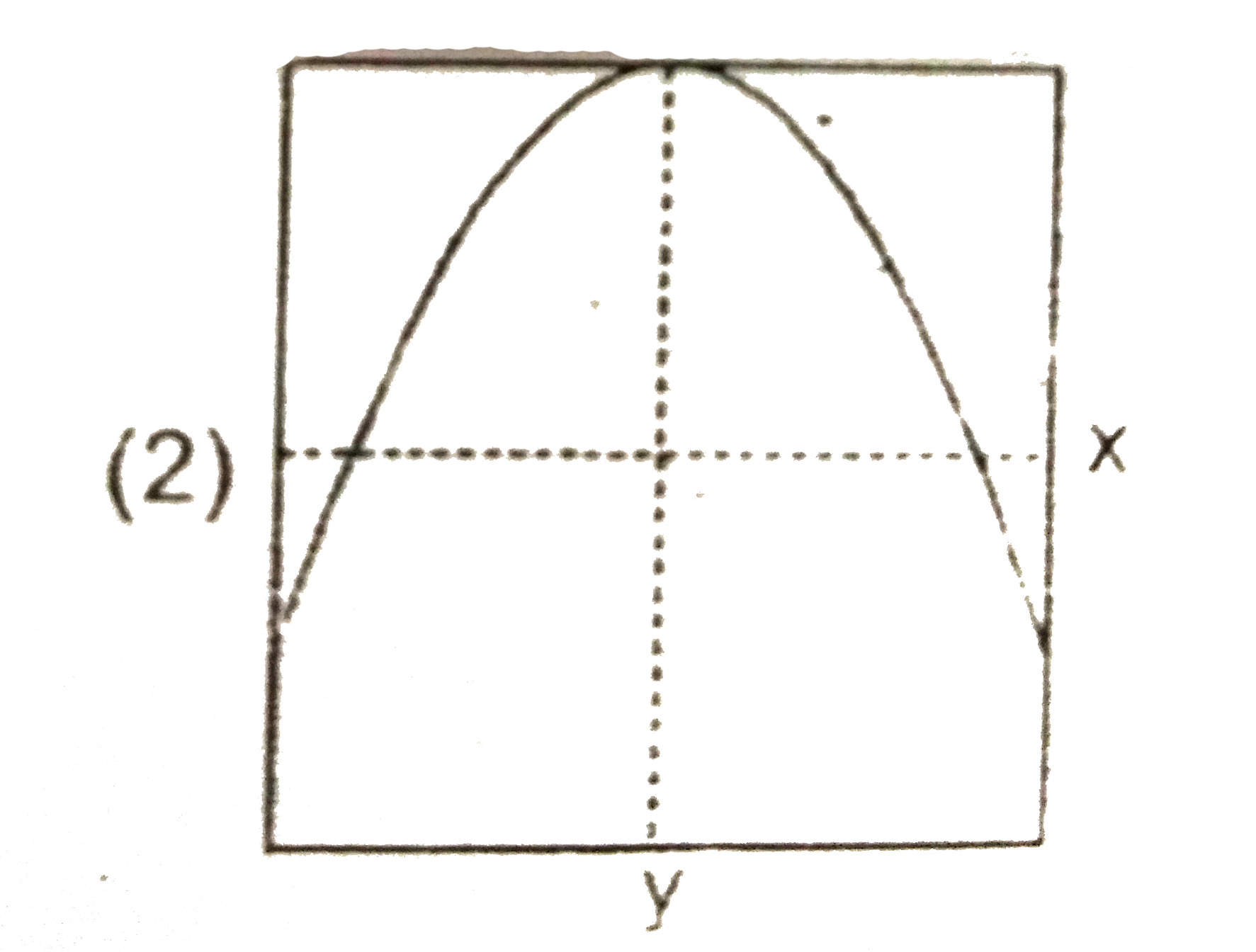
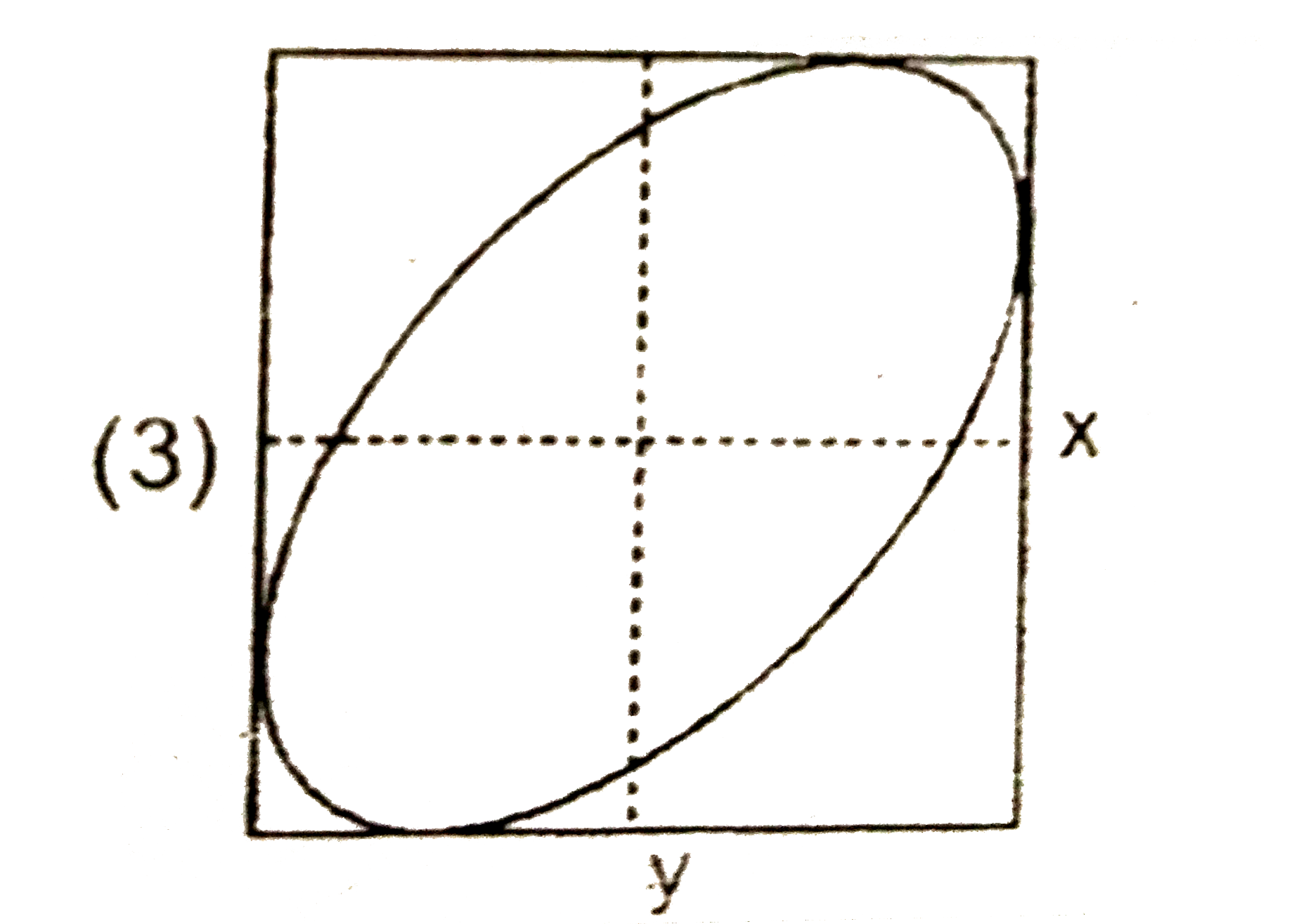
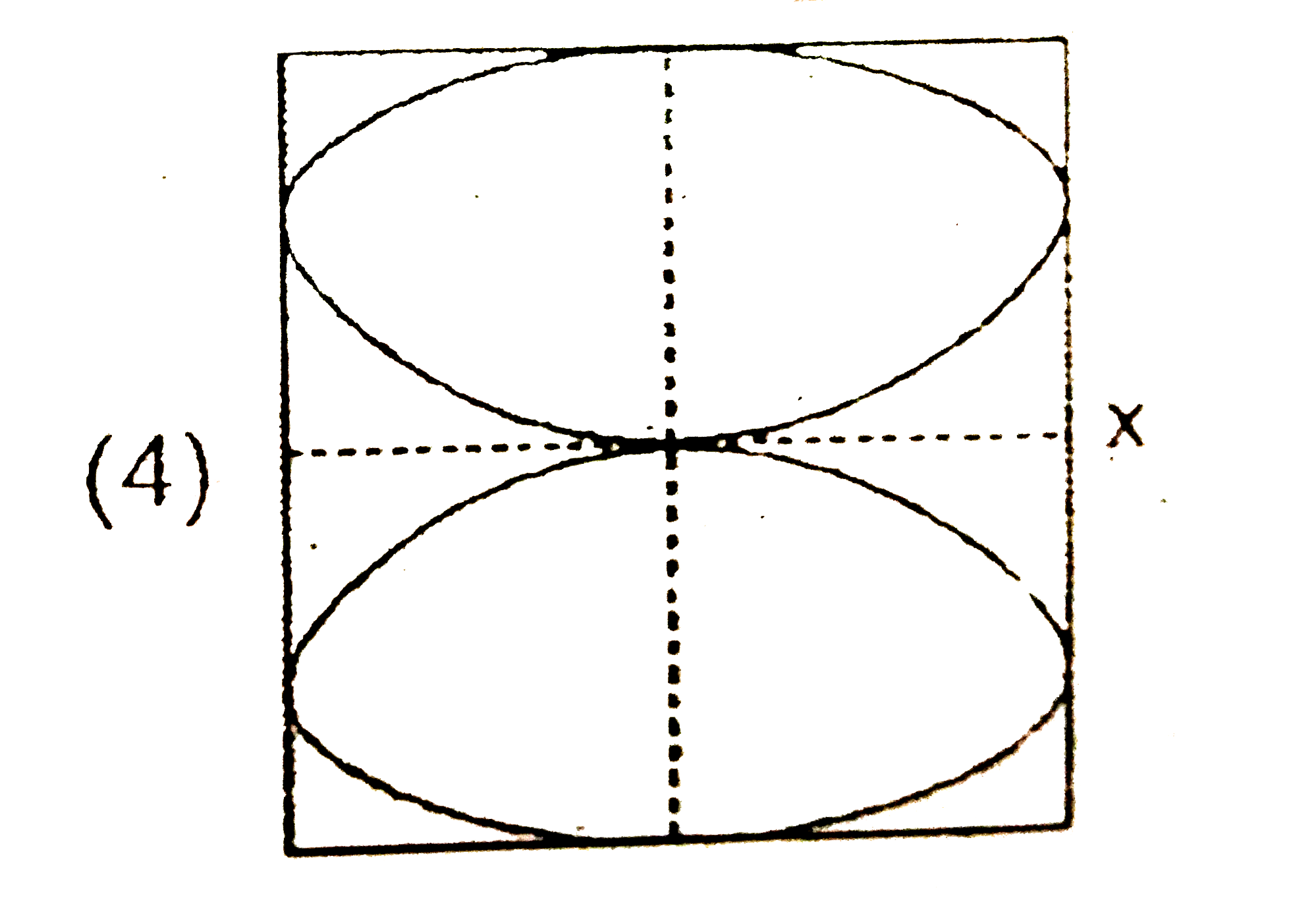
The correct Answer is:A
To determine the trajectory of the particle given the displacements x(t)=−asin(ωt) and y(t)=asin(2ωt), we can follow these steps:
Step 1: Analyze the equations
The equations for the displacements are:
- x(t)=−asin(ωt)
- y(t)=asin(2ωt)
Step 2: Find critical points
We will evaluate the displacements at specific time intervals to understand the trajectory.
At t=0:
- x(0)=−asin(0)=0
- y(0)=asin(0)=0
So, at t=0, the particle is at the origin (0,0).
Step 3: Evaluate at t=π2ω
At t=π2ω:
- x(π2ω)=−asin(ω⋅π2ω)=−asin(π2)=−a
- y(π2ω)=asin(2ω⋅π2ω)=asin(π)=0
At this point, the particle is at (-a, 0).
Step 4: Evaluate at t=π4ω
At t=π4ω:
- x(π4ω)=−asin(π4)=−a⋅√22=−a√22
- y(π4ω)=asin(π2)=a
At this point, the particle is at −a√22,a.
Step 5: Evaluate at t=π2ω
At t=π2ω:
- x(π2ω)=−asin(π)=0
- y(π2ω)=asin(2π)=0
The particle returns to the origin (0,0).
Step 6: Evaluate at t=3π4ω
At t=3π4ω:
- x(3π4ω)=−asin(3π4)=−a⋅√22=−a√22
- y(3π4ω)=asin(3π2)=−a
At this point, the particle is at −a√22,−a.
Step 7: Evaluate at t=2πω
At t=2πω:
- x(2πω)=−asin(2π)=0
- y(2πω)=asin(4π)=0
The particle returns to the origin (0,0).
Conclusion
By plotting these points, we can see that the trajectory of the particle forms a closed loop. The trajectory will look like a sinusoidal wave pattern in the x-y plane.
The equations for the displacements are:
- x(t)=−asin(ωt)
- y(t)=asin(2ωt)
We will evaluate the displacements at specific time intervals to understand the trajectory.
- x(0)=−asin(0)=0
- y(0)=asin(0)=0
At t=π2ω:
- x(π2ω)=−asin(ω⋅π2ω)=−asin(π2)=−a
- y(π2ω)=asin(2ω⋅π2ω)=asin(π)=0
At t=π4ω:
- x(π4ω)=−asin(π4)=−a⋅√22=−a√22
- y(π4ω)=asin(π2)=a
At t=π2ω:
- x(π2ω)=−asin(π)=0
- y(π2ω)=asin(2π)=0
At t=3π4ω:
- x(3π4ω)=−asin(3π4)=−a⋅√22=−a√22
- y(3π4ω)=asin(3π2)=−a
At t=2πω:
- x(2πω)=−asin(2π)=0
- y(2πω)=asin(4π)=0
By plotting these points, we can see that the trajectory of the particle forms a closed loop. The trajectory will look like a sinusoidal wave pattern in the x-y plane.
Similar Questions
Knowledge Check
The displacement of a particle is given by x=cos2ωt. The motion is
Asimple harmonicBperiodic but not simple harmonicCperiodic but not simple harmonicDNone of the aboveThe displacemeent of a particle is given at time t by x=Asin(−2ωt)+Bsin2ωt. Then,
Athe motion of the particle is SHM with an amplitude of √A2+B24Bthe motion of the particle is not SHM, but oscillatory with a time period of T=πω.Cthe motion of the particle is oscillatory with a time period of T=π2ω.Dthe motion of the particle is a not periodicThe displacement of a particle is given at time t, by:
x=Asin(−2ωt)+Bsin2ωt Then,Athe motion of the particle is SHM with an amplitude of √A2+B24Bthe motion of the particle is not SHM, but oscillatory with a time period of T=π/ωCthe motion of the particle is oscillatory with a time period of T=π/2ωDnone
A particle is acted simultaneously by mutually perpendicular simple hormonic motions x=acosωtandy=asinωt. The trajectory of motion of the particle will be
View SolutionA particle is acted simultaneously by mutually perpendicular simple harmonic motions x=a cosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is

View SolutionA particle is acted simultaneously by mutally perpendicular simple harmonic motion x=acosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionA particle moves in x-y plane according to rule x=asinωt and y=−acosωt. The particle follows
View Solution