Consider a solid sphere placed in surrounding with small temperature difference between sphere's surface and surrounding. If ΔT and r represent temperature difference (between sphere and surrounding) and radius of sphere respectively, rate of cooling of the sphere is directly proportional to:
(ΔT)4
ΔT
r2
1r
The correct Answer is:B, D
rate of cooling =4eσAΔTms if ΔT is small
=4eσ(4πr2)ΔTρ343πr3s
Similar Questions
Knowledge Check
A solid sphere and a hollow sphere of the same material and size are heated to the same temperature and allowed to cool in the same surroundings. If the temperature difference between the surroundings and each sphere is T, then :
AThe hollow sphere will cool at a faster rate for all values of TBThe solid sphere will cool at a faster rate for all values of TCBoth spheres will cool at the same rate for all values of TDBoth spheres will cool at the same rate only for small values of TFor a small temperature difference between the body and the surroundings the relation between the rate of loss heat R and the temperature of the body is depicted by
A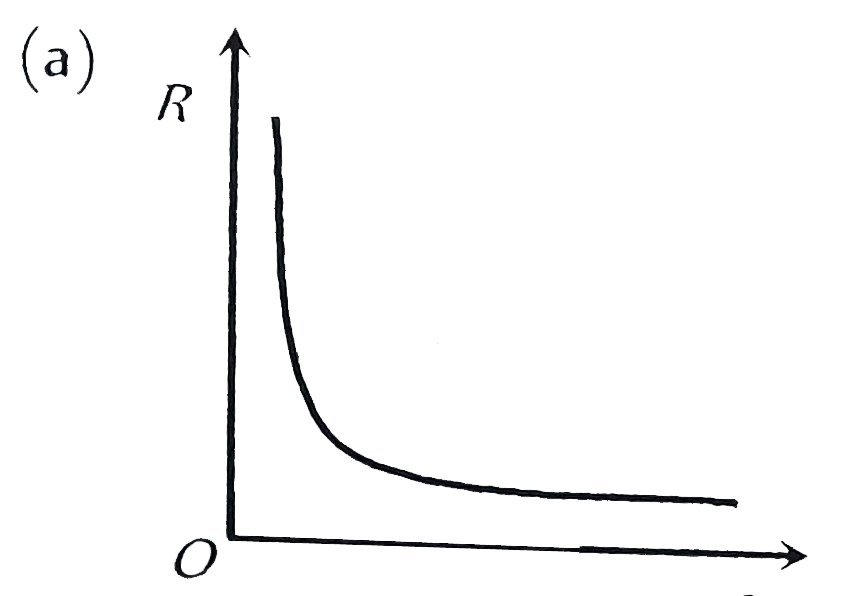 B
B C
C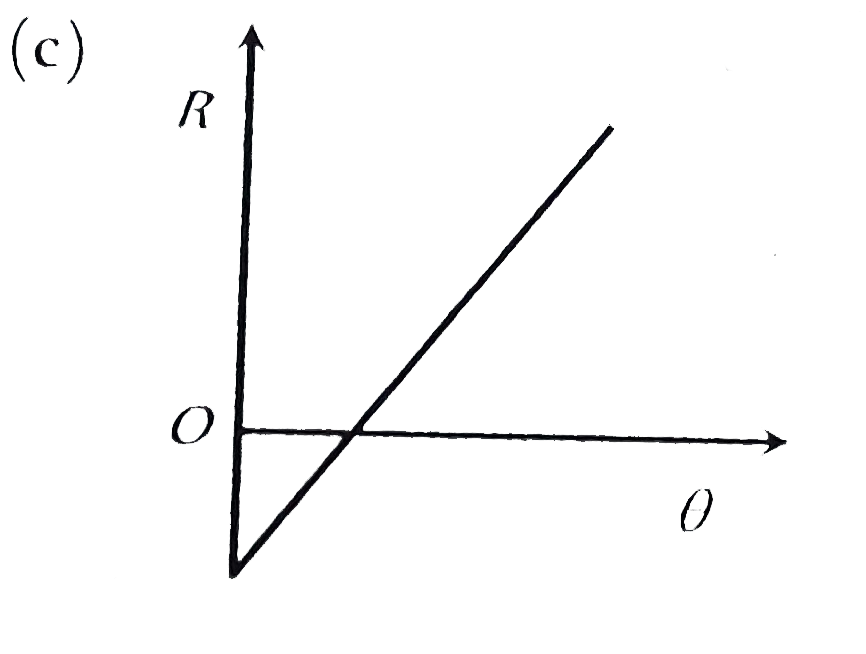 D
D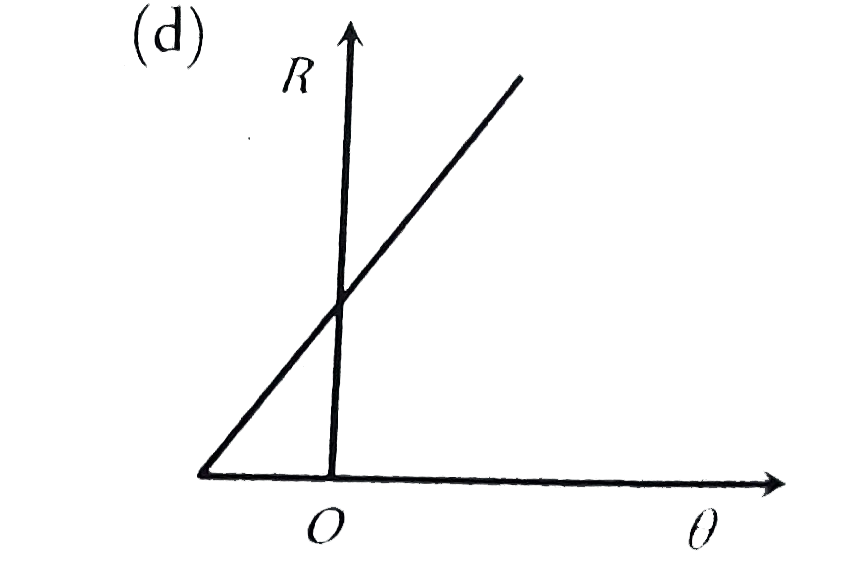
As difference of temperature of body and surroundings increases, rate of cooling
AincreasesBdecreasesCdoes not depend on itDincreases or decreases
For a small temperature difference between the body and the surroundings, the relation between the rate of heat loss R and the temperature of the body is depicted by
View SolutionA sphere of density d, specific heat s and radius r is hung by a thermally insulating thread in an enclosure which is kept at a lower temperature than the sphere. The temperature of the sphere starts to drop at a rate which depends upon the temperature difference between the sphere and the enclosure. If the temperature difference is ΔT and surrounding temperature is T0 then rate of fall in temperature will be
[Given that ΔT<<T0]
View SolutionA sphere of density d, specific heat s and radius r is hung by a thermally insulating thread in an enclosure which is kept at a lower temperature than the sphere. The temperature of the sphere starts to drop at a rate which depends upon the temperature difference between the sphere and the enclosure. If the temperature difference is ΔT and surrounding temperature is T0 then rate of fall in temperature will be
[Given that ΔT<<T0]
View SolutionThe rates of fall temperature of two identical solid spheres of different materials are equal at a certain temperature if:
View SolutionFor a sphere made out of a certain material, the moment of inertia of the sphere is proportional to [ radius of the sphere = R ]
View Solution