Find the total number of stereoisomers of [M(gly)3]
[Where M is any metal capable of forming such complexes.]
The correct Answer is:4
To find the total number of stereoisomers of the complex (M(gly)3) where M is a metal that can form such complexes, we can follow these steps:
Step 1: Identify the ligand and its properties
Glycine (gly) is a bidentate ligand, meaning it has two donor atoms that can coordinate to the metal center. In glycine, the donor atoms are the nitrogen (N) and the oxygen (O) atoms.
Hint: Remember that bidentate ligands can create different geometric arrangements around the metal center.
Step 2: Determine the possible geometric isomers
For octahedral complexes with three bidentate ligands, we can have two types of geometric isomers: facial (fac) and meridional (mer).
- Facial (fac): The three bidentate ligands occupy adjacent positions around the metal center.
- Meridional (mer): The three bidentate ligands occupy positions such that one ligand is opposite another.
Hint: Visualize the arrangement of ligands around the metal to differentiate between facial and meridional isomers.
Step 3: Count the geometric isomers
In this case, we can have:
- 2 geometric isomers: 1 facial and 1 meridional.
Hint: Draw the structures of both isomers to see how the ligands are arranged differently.
Step 4: Determine optical activity
Next, we need to check for optical isomers (enantiomers).
- The facial isomer can exist in two enantiomeric forms (optically active).
- The meridional isomer can also exist in two enantiomeric forms (optically active).
Hint: Look for a plane of symmetry in the structures; if none exists, the isomer is likely optically active.
Step 5: Calculate the total number of stereoisomers
Since both the facial and meridional isomers have two enantiomers each, we can calculate the total number of stereoisomers as follows:
- 2 (facial isomers) + 2 (meridional isomers) = 4 stereoisomers in total.
Hint: Remember to sum all the unique isomers to get the final count.
Final Answer
The total number of stereoisomers of (M(gly)3) is 4.
Glycine (gly) is a bidentate ligand, meaning it has two donor atoms that can coordinate to the metal center. In glycine, the donor atoms are the nitrogen (N) and the oxygen (O) atoms.
For octahedral complexes with three bidentate ligands, we can have two types of geometric isomers: facial (fac) and meridional (mer).
- Meridional (mer): The three bidentate ligands occupy positions such that one ligand is opposite another.
In this case, we can have:
- 2 geometric isomers: 1 facial and 1 meridional.
Next, we need to check for optical isomers (enantiomers).
- The facial isomer can exist in two enantiomeric forms (optically active).
- The meridional isomer can also exist in two enantiomeric forms (optically active).
Since both the facial and meridional isomers have two enantiomers each, we can calculate the total number of stereoisomers as follows:
- 2 (facial isomers) + 2 (meridional isomers) = 4 stereoisomers in total.
The total number of stereoisomers of (M(gly)3) is 4.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBook:GRB PUBLICATIONChapter:COORDINATION COMPOUNDSExercise:MATCH THE COLUMN TYPE
Explore 41 Videos
- CHEMICAL KINETICSBook:GRB PUBLICATIONChapter:CHEMICAL KINETICSExercise:Subjective Type
Explore 63 Videos
- D-BLOCK ELEMENTSBook:GRB PUBLICATIONChapter:D-BLOCK ELEMENTSExercise:Subjective Type
Explore 18 Videos
Similar Questions
Knowledge Check
The total number of stereoisomers of 2, 3-pentanediol are
AfourBtwoCsixDthree
The total number of stereoisomers that can exist for M is

View SolutionThe total number of stereoisomers that can exist for M is

View SolutionThe total number of stereoisomers that can exist for M is
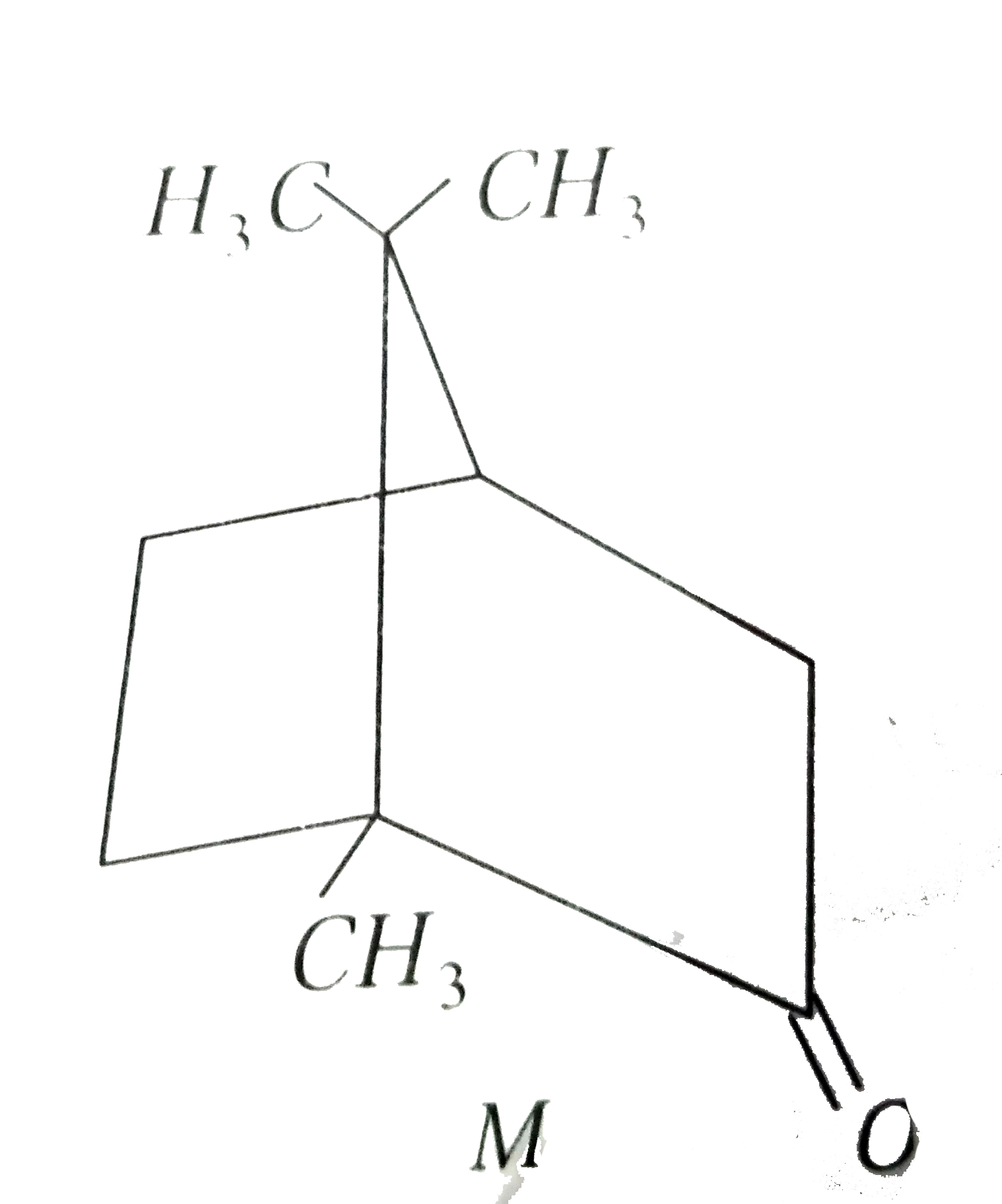
View SolutionThe total number of stereoisomers that can exist for M is
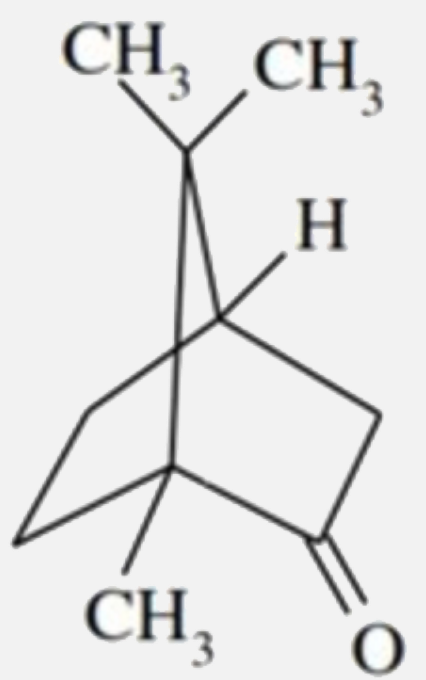
View Solution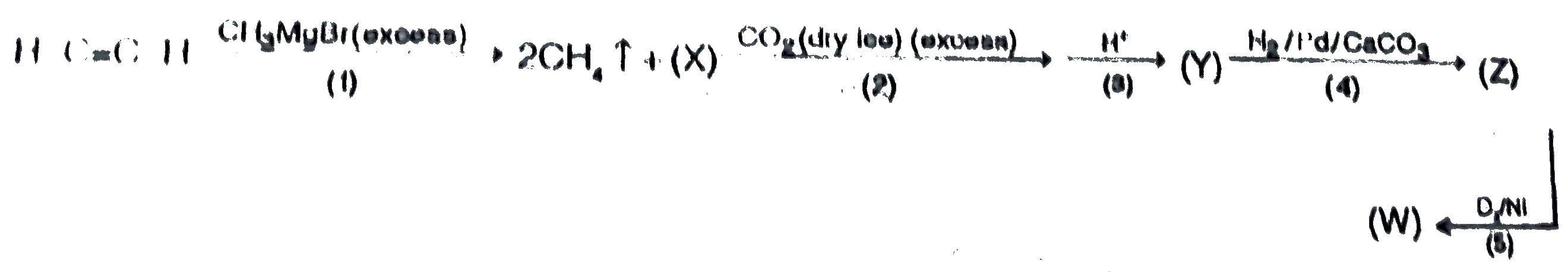
The total number of stereoisomers formed at the end product 'W' is :
View SolutionFind the total number of geometrical iosmers of [M(AB)(CD)(EF)]n+
View SolutionFind the total number of geometrical iosmers of [M(AB)(CD)(EF)]n+
View Solution


