Unlike a laboratory sonometer, a stringed instrument is seldom plucked in the middle. Supposing a sitar string is plucked at about 14th of its length from the end. The most prominent harmonic would be
Eighth
Fourth
Third
Second
The correct Answer is:D
To determine the most prominent harmonic when a sitar string is plucked at about 14th of its length from the end, we can follow these steps:
Step 1: Understand the setup
A sitar string is fixed at both ends, which means it can vibrate in certain modes or harmonics. When plucked, the string will form standing waves with nodes and antinodes.
Step 2: Identify the point of plucking
Plucking the string at 14th of its length from one end means that this point will be an antinode (the point of maximum displacement).
Step 3: Determine the positions of nodes and antinodes
Since the string is fixed at both ends, the nodes will be at the ends (0 and L) and at the midpoint (L/2). Given that we have an antinode at 14L, we can visualize the standing wave pattern:
- Antinode at 14L
- Node at 12L
- Antinode at 34L
- Node at L
Step 4: Count the number of loops
In this configuration, we can see that there are two antinodes and three nodes:
- The first antinode is at 14L
- The second antinode is at 34L
This configuration corresponds to the second harmonic, which has one complete loop (or segment) between the two nodes.
Step 5: Conclusion
Thus, the most prominent harmonic when the sitar string is plucked at 14th of its length from the end is the second harmonic.
Final Answer
The most prominent harmonic would be the second harmonic.
---
A sitar string is fixed at both ends, which means it can vibrate in certain modes or harmonics. When plucked, the string will form standing waves with nodes and antinodes.
Plucking the string at 14th of its length from one end means that this point will be an antinode (the point of maximum displacement).
Since the string is fixed at both ends, the nodes will be at the ends (0 and L) and at the midpoint (L/2). Given that we have an antinode at 14L, we can visualize the standing wave pattern:
- Antinode at 14L
- Node at 12L
- Antinode at 34L
- Node at L
In this configuration, we can see that there are two antinodes and three nodes:
- The first antinode is at 14L
- The second antinode is at 34L
Thus, the most prominent harmonic when the sitar string is plucked at 14th of its length from the end is the second harmonic.
The most prominent harmonic would be the second harmonic.
Topper's Solved these Questions
- WAVES AND SOUNDBOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - Assertion and Reason
16 Videos
- VECTORSBOOK - ERRORLESS CHAPTER - VECTORSEXERCISE - Exercise
223 Videos
- WORK , ENERGY , POWER AND COLLISIONBOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Self Evaluation Test
19 Videos
Similar Questions
We have a stringed musical instrument. The string is plucked in the middle first with a force of greater magnitude and then with a force of smaller magnitude. In which case would the instrument produce a louder sound?
View SolutionWe have a stringed musical instrument. The string is plucked in the middle first with a force of greater magnitude and then with a force of smaller magnitude. In which case would the instrument produce a louder sound?
View Solution
Knowledge Check
A sonometer is plucked at 1/4 of its length . The most prominent would be
AEightBFourthCThirdDSecondChoose the most appropriate option.
A stretched string of length 1 m fixed at both ends, when vibrated in one loop has a frequency 200 Hz. It is now plucked at a point situated at 25 cm from one end. The stretched string would vibrate with a frequency ofA100 HzB200 HzC400 HzD800 HzA stretched string of length 1m fixed at both ends , having a mass of 5×10−4kg is under a tension of 20N. It is plucked at a point situated at 25cm from one end . The stretched string would vibrate with a frequency of
A400HzB100HzC200HzD256Hz
A solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as 5th turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden.
(a) Find the angular speed of the sphere as the string leaves it.
(b) Find the change in acceleration of the small mass m after 5 turns get unwound from the sphere.
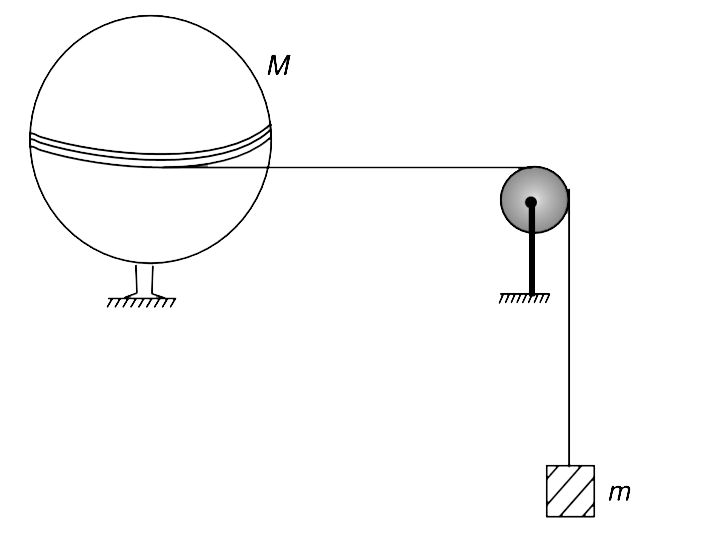
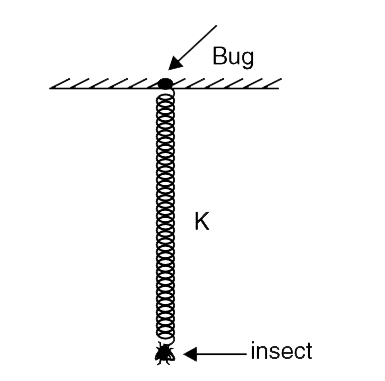
View SolutionA massless spring of force constant K and natural length l0 is hanging from a ceiling. An insect of mass m is sitting at the lower end of the spring and the system is in equilibrium . The insect starts slowing climbing up the spring so as to eat a bug sitting on the ceiling. Assume that insect climbs without slipping on the spring and K=mgl0 . find the length of the spring when the insect is at 14th of its original distance from the bug .
View SolutionA rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance 5a4 from the axes. If the coefficient of friction is 13 and the particle remains at rest relative to the plane, show that w≤√4g15a. The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance 5a4, show that the greatest possible angular velocity is √1315.ga and find the least possible velocity.
View SolutionThe first overtone of a pipe closed at one end resonates with the third harmonic of a string fixed at its ends. The ratio of the speed of sound to the speed of transverse wave travelling on the string is 2 : 1. Find the ratio of the length of pipe to the length of string.
View SolutionTension of a string is 6.4 N and load is applied to it at its lower end of a string is 0.1 kg .If the length of string is 6 m , then its angular velocity will be
View Solution
