Read the following passage carefully and answer the questions

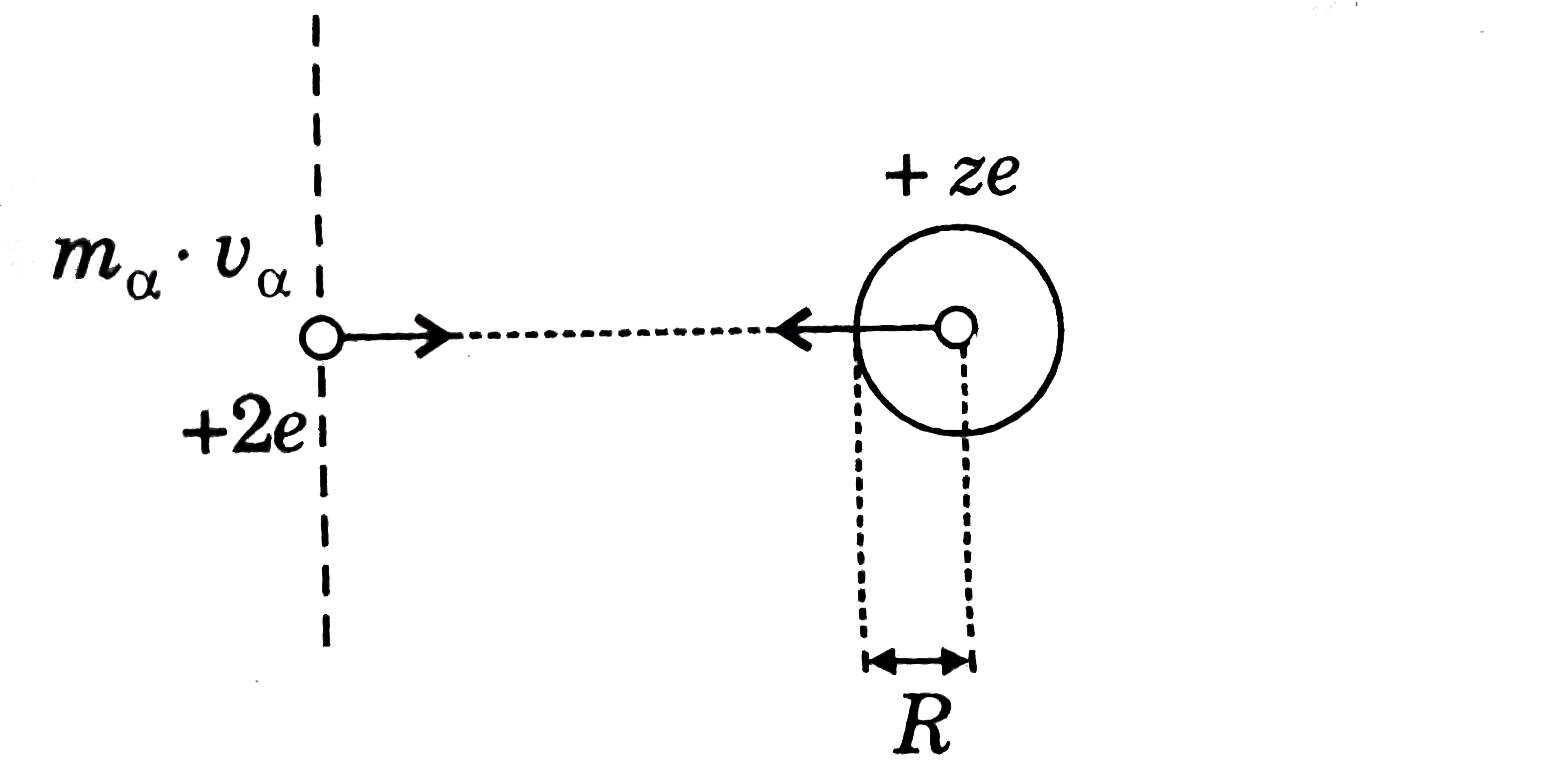
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's $α -$ scattering experiment. If an $α -$ perticle is projected from infinity with speed v, towards the nucleus having z protons then the $a p h a -$ perticle which is reflected back or which is deflected by $180^{\circ}$ must have approach closest to the nucleus. It can be approximated that $α -$ particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
${(Total Energy)}_{initial} = {(Total Enregy)}_{final}$
${(K E)}_{i} + {(P E)}_{i} = {(K E)}_{f} + {(P E)}_{f}$
${(P E)}_{i} = 0, since P E$ of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
$\frac{1}{2} m_{α} v_{α}^{2} + 0 = 0 + \frac{k q_{1} q_{2}}{R}$
$\Rightarrow \frac{1}{2} m_{α} v_{α}^{2} = k \frac{2 e \times z e}{R} \Rightarrow R = \frac{4 k z e^{2}}{m_{α} v_{α}^{2}}$
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
$R = R_{0} {(A)}^{1 / 3}$
where $R_{0} = 1.2 \times 10^{- 15} m$
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of $α -$ particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , $α -$ particle with half of the earlier speed then the percentage error involved in the radius calculation is :

0.75

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha-scattering experiment. If an alpha-perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha-perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha-particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus Radius of a particular nucleus is calculated by the projection of alpha-particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , alpha-particle with half of the earlier speed then the percentage error involved in the radius calculation is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 CHEMISTRY STRUCTURE OF ATOM

Topper's Solved these Questions

Knowledge Check

Read the following passage carefully and answer the questions

The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's $α -$ scattering experiment. If an $α -$ perticle is projected from infinity with speed v, towards the nucleus having z protons then the $a p h a -$ perticle which is reflected back or which is deflected by $180^{\circ}$ must have approach closest to the nucleus. It can be approximated that $α -$ particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
${(Total Energy)}_{initial} = {(Total Enregy)}_{final}$
${(K E)}_{i} + {(P E)}_{i} = {(K E)}_{f} + {(P E)}_{f}$
${(P E)}_{i} = 0, since P E$ of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
$\frac{1}{2} m_{α} v_{α}^{2} + 0 = 0 + \frac{k q_{1} q_{2}}{R}$
$\Rightarrow \frac{1}{2} m_{α} v_{α}^{2} = k \frac{2 e \times z e}{R} \Rightarrow R = \frac{4 k z e^{2}}{m_{α} v_{α}^{2}}$
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
$R = R_{0} {(A)}^{1 / 3}$
where $R_{0} = 1.2 \times 10^{- 15} m$
A= atomic mass number
R=radius of nucleus
If the diameter of two different nuclei are in the ratio 1:2 then their mass number are in the ratio:
A0.043055555555556
B0.33402777777778
C0.047222222222222
D0.044444444444444
Read the following passage carefully and answer the questions

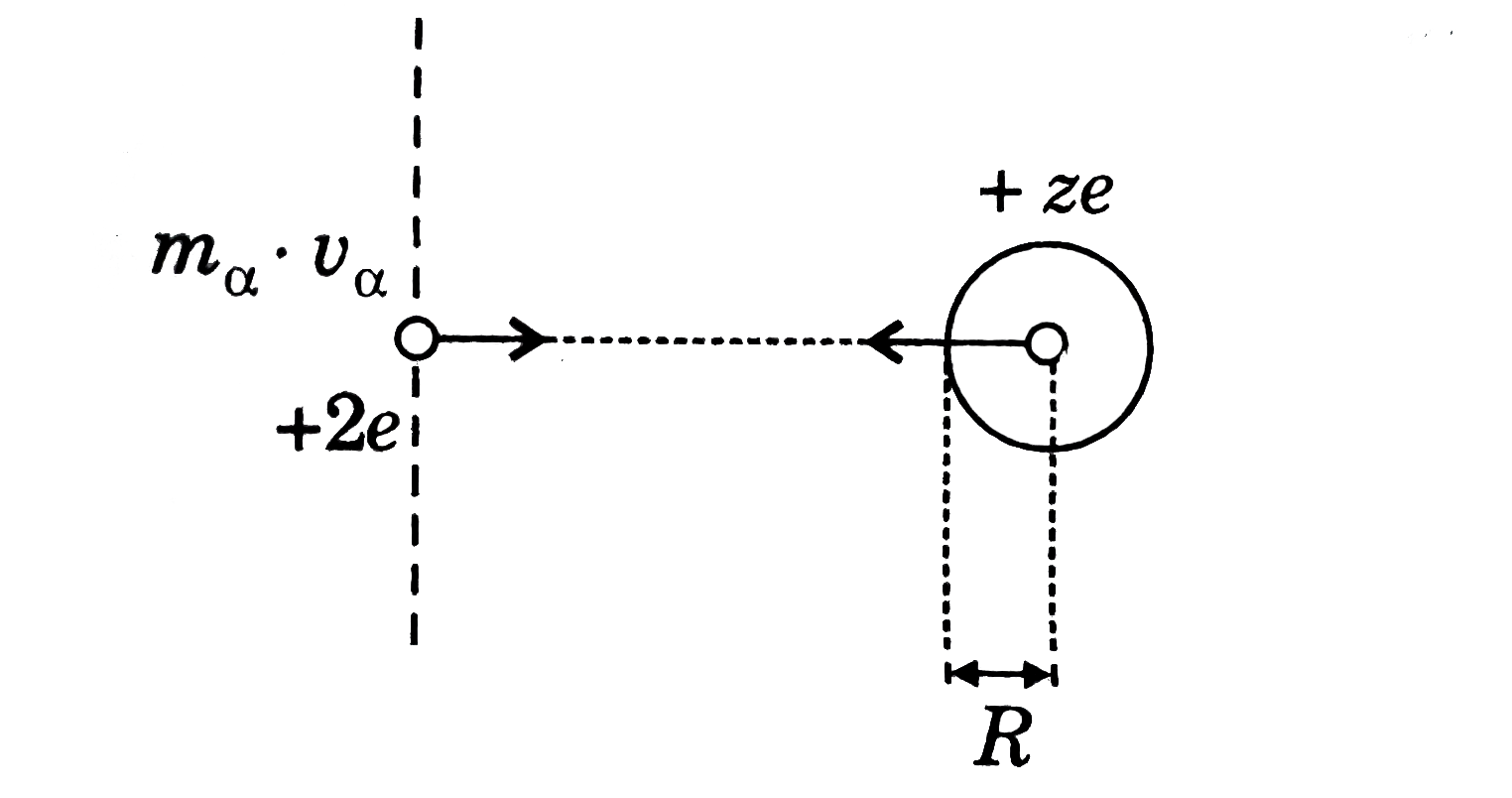
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's $α -$ scattering experiment. If an $α -$ perticle is projected from infinity with speed v, towards the nucleus having z protons then the $a p h a -$ perticle which is reflected back or which is deflected by $180^{\circ}$ must have approach closest to the nucleus. It can be approximated that $α -$ particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
${(Total Energy)}_{initial} = {(Total Enregy)}_{final}$
${(K E)}_{i} + {(P E)}_{i} = {(K E)}_{f} + {(P E)}_{f}$
${(P E)}_{i} = 0, since P E$ of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
$\frac{1}{2} m_{α} v_{α}^{2} + 0 = 0 + \frac{k q_{1} q_{2}}{R}$
$\Rightarrow \frac{1}{2} m_{α} v_{α}^{2} = k \frac{2 e \times z e}{R} \Rightarrow R = \frac{4 k z e^{2}}{m_{α} v_{α}^{2}}$
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
$R = R_{0} {(A)}^{1 / 3}$
where $R_{0} = 1.2 \times 10^{- 15} m$
A= atomic mass number
R=radius of nucleus
If $α -$ particle with speed $v_{0}$ is projected from infinity and it approaches upto $r_{0}$ distance from the nuclei. Then the speed of $α -$ particle which approaches $2 r_{0}$ distance from the nucleus is
A $\sqrt{2} v_{0}$
B $\frac{v_{0}}{\sqrt{2}}$
C $2 v_{0}$
D $\frac{v_{0}}{2}$
Rutherford's $α$ - scattering experiment related to the size of the-
Anucleus
Batom
Celectron
Dneutron

GRB PUBLICATION-ATOMIC STRUCTURE-Comprehesion Type

Home
Ask Doubt
Profile

The correct Answer is:c

Topper's Solved these Questions

Similar Questions

Knowledge Check

Rutherford's α- scattering experiment related to the size of the-

GRB PUBLICATION-ATOMIC STRUCTURE-Comprehesion Type

Rutherford's $α$ - scattering experiment related to the size of the-