Ψ(r)=ke−r/k1.r2(r2−k2r+k3) . If the orbital has no nodal plane , then , orbital can be :
5dxy
5d
4dz2
4px
The correct Answer is:A
Step by step video, text & image solution for Psi_((r)) = ke^(-r//k_(1)) dot" r^(2) (r^(2) - k_(2)r + k_(3)) . If the orbital has no nodal plane , then , orbital can be : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:Reasoning Type
Explore 11 Videos
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:Multiple Objective Type
Explore 49 Videos
- ATOMIC STRUCTUREBook:GRB PUBLICATIONChapter:ATOMIC STRUCTUREExercise:de Brogile and Heisenberg
Explore 43 Videos
- CHEMICAL EQUILIBRIUMBook:GRB PUBLICATIONChapter:CHEMICAL EQUILIBRIUMExercise:D.Le Chateliera principle
Explore 16 Videos
Similar Questions
Mr. Santa has to decode a number “ABCDEF” where each alphabet is represented by a single digit. Suppose an orbital whose radial wave functional is represented as :
ψ(r)=k1e−r/k2(r2−5k3r+6k23)
From the following information given about each alphabet then write down the answers in the form of “ABCDEF”, for above orbital.
Info A = Value of n where “n” is principal quantum number.
Info B = No. of angular nodes
Info C = Azimuthal quantum number of subshell to orbital belongs
Info D = No. of subshells having energy between (n+5) s to (n+5) p where n is principal quantum number.
Info E = Orbital angular momentum of given orbital.
Info F = Radial distance of the spherical node which is farthest from the nucleus.
(Assuming k3=1))
View SolutionΨr=k1e−r/k2(r2−5k3r+6K23)
For the above orbital match the column-I with column-II (assuming ,k3=1)

View Solution
Knowledge Check
A 4πr2Ψ2(r)vs r is ploted for H-orbital curve contains '3'maxima . If orbital contains 2 angular node then orbital is
A5dB4dC5pD4pThe orbital velocity of a satellite at point B with radius rB and n. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes .12rA find the orbital velocity at (1.2rA):
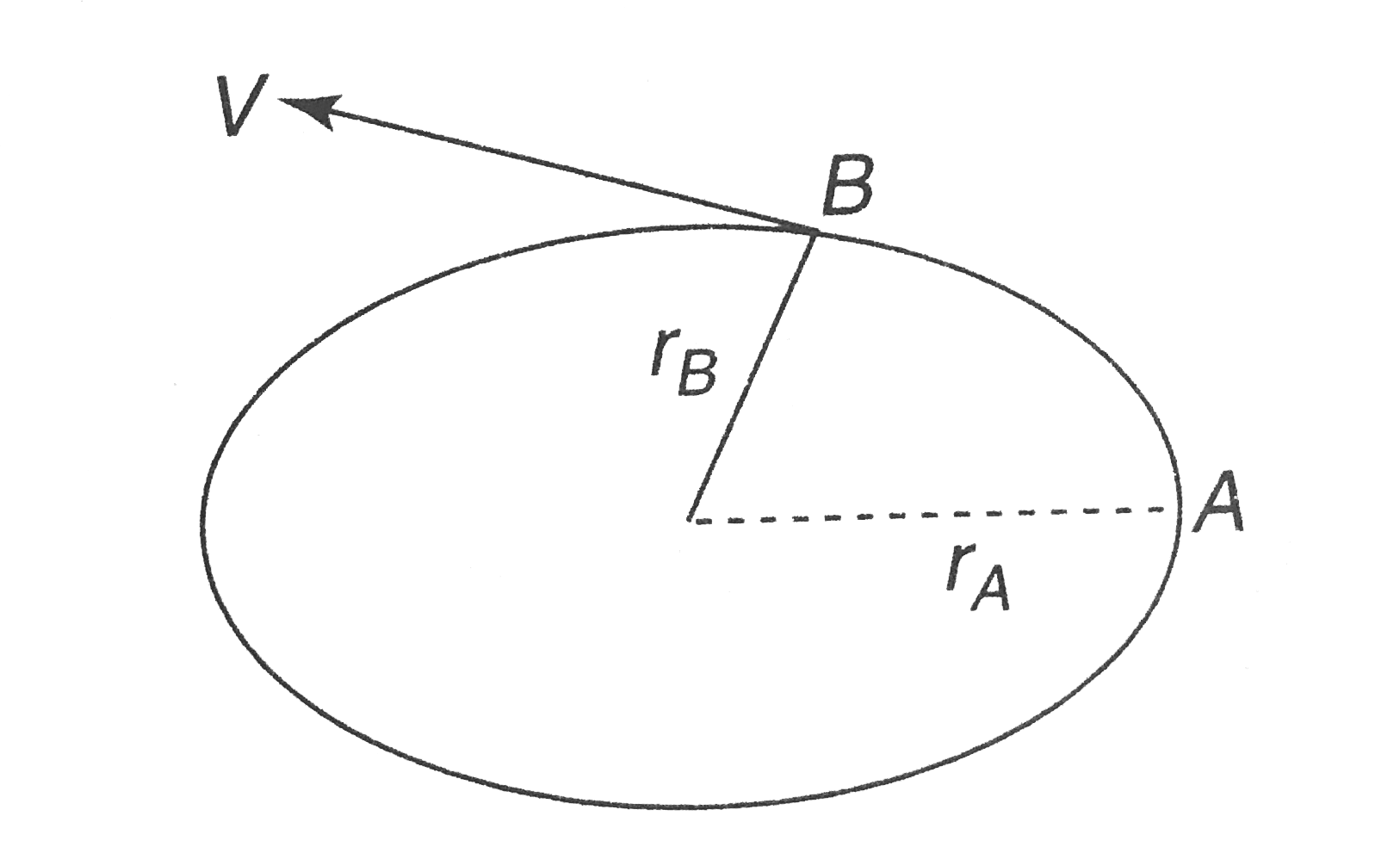 AvrBrA√1.2BvrA1.2rBCvrB1.2rADvrArB√2
AvrBrA√1.2BvrA1.2rBCvrB1.2rADvrArB√2If nCr−1=(k2−8)(n+1Cr), then k belongs to
A[−3,−2√2)B(−3,3)C[−3,−2√2)∪(2√2,3]D[−2√2,2√2]
Mr.Santa has to decode a number "ABCDEF" where each alphabet is respersented by a single digit .
Suppose an orbital whose radial wave functoin id respresented as
Ψr=K1.e_r/k2(r2−5k3r+k23)
From the following information given about each alphabet then write down the answer in the from of
"ABCDEF" , for above orbital .
Info A= Value of n where "n" is principle quantum number
Info B= No .of angular nodes
InfoC=Azimuthal quantum number of subshell to orbital belongs
Info D= No. of subshells having energy between (n+5)s to (n+5)p where n id principle quantum
number
Info E=Orbital angular momentum of given orbital.
Info F= Radial distance of the spherical node which is farthest from the nuclues
(Assuming K3 =1)
View SolutionThe wave function of 2s electron is given by
ψ2s=14√2π(1a0)3/2(2−ra0)e−ra0
It has a node at r=rp . Find the relation between rp and a.
View SolutionIn a triangle ABC, if (r1+r2)(r2+r3)(r3+r1)=4RK then k=
View SolutionLetSK=k∑r=1tan−1(6r22r+1+32r+1). Then limk→∞Sk is equal to :
View SolutionFor an orbital , having no planar angular nodes following the equation :
Ψ(r)=Ke−r/K'.r2(K''−r)
Identify the orbital :
View Solution

