Four particles given have same momentum which has maximum kinetic energy
Proton
Electron
Deutron
α-particle
The correct Answer is:B
Step by step video, text & image solution for Four particles given have same momentum which has maximum kinetic energy by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
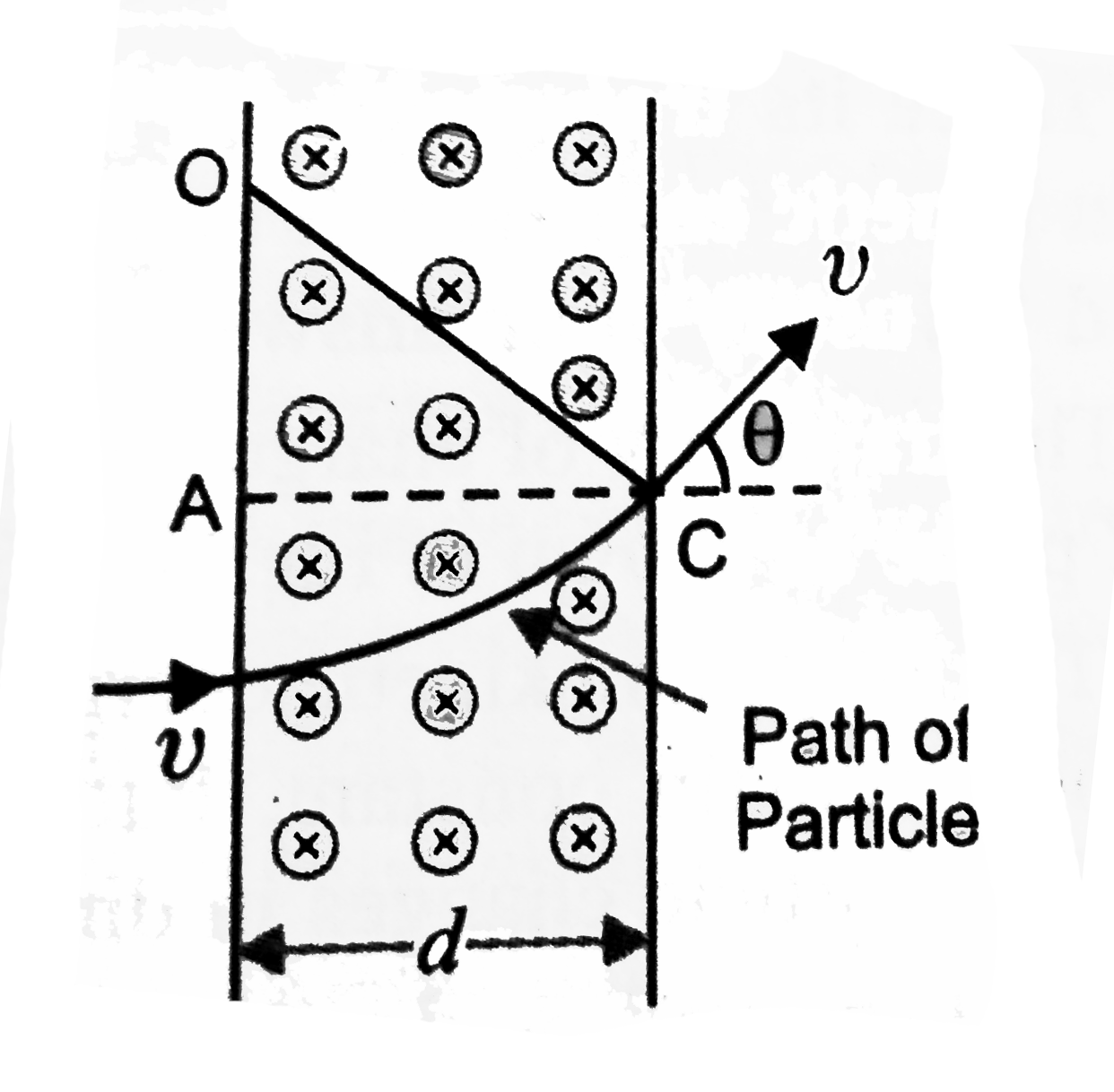
A proton and an alpha particle are projected in a perpendicular magnetic field B which exists in a region of width d, figure. Find the ratio of the sines of angles of deviation suffered by the proton and the alpha particle if before entering the magnetic field both the particles (i) have the same momentum (ii) have the same kinetic energy.
View SolutionA light and a heavy object have the same momentum. Find out the ratio of their kinetic energies. Which one has a larger kinetic energy ?
View Solution
Knowledge Check
A single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum kinetic energy of the particle and the value of x at which maximum kinetic energy occurs areA(a) 29J,0mB(b) 49J,0mC(c) 49J,2mD(d) 29J,2mA beta particle, gamma ray, and alpha particle all have the same momentum. Which has the longest wavelength?
ABeta particleBGamma rayCAlpha particleDAll the sameAssertion: A light body and a heavy body have same momentum. Then they also have same kinetic energy.
Reason: Kinetic energy does not depand on mass of the body.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion and reason are false.
Two bodies of masses m1 and m2 have the same linear momentum. What is the ratio of their kinetic energies?
View SolutionAssertion: A light body and a heavy body have same momentum. Then they also have same kinetic energy.
Reason: Kinetic energy does not depand on mass of the body.
View SolutionThe particle executing simple harmonic motion has a kinetic energy K0cos2ωt. The maximum values of the potential energy and the energy are respectively
View SolutionThe particle executing simple harmonic motion has a kinetic energy K0cos2ωt. The maximum values of the potential energy and the total energy are respectively:
View SolutionA particle of mass m has momentum p. Its kinetic energy will be
View Solution

