Three weights W , 2 W and 3 W are connected to identical springs suspended from a rigid horizontal rod. The assembly of the rod and the weights fall freely. The positions of the weights from the rod are such that
3 W will be farthest
W will be farthest
All will be at the same distance
2 W will be farthest
The correct Answer is:C
Step by step video, text & image solution for Three weights W , 2 W and 3 W are connected to identical springs suspended from a rigid horizontal rod. The assembly of the rod and the weights fall freely. The positions of the weights from the rod are such that by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Graphical Questions
Explore 11 Videos
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Assertion & Reason
Explore 25 Videos
- NEWTONS LAWS OF MOTIONBook:ERRORLESS Chapter:NEWTONS LAWS OF MOTIONExercise:Motion of Connected Bodies
Explore 23 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
- ROTATIONAL MOTIONBook:ERRORLESS Chapter:ROTATIONAL MOTIONExercise:Practice Problems (Problems based on motion of connected mass)
Explore 10 Videos
Similar Questions
Knowledge Check
Three weights w, 2w and 3w are connected to identical spring suspended from a rigid horizontal rod. The assembly of the rod and the weights fall freely. The positions of the weight from the rod are such that
A3w will be farthestBw will be farthestCall will be at the same distanceD2w will be farthestA body of weight w1 is suspended from the ceiling of a room through as chain of weight w2. The ceiling pulls the chain by a force
Aw1Bw2Cw1+w2Dw1+w22A spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
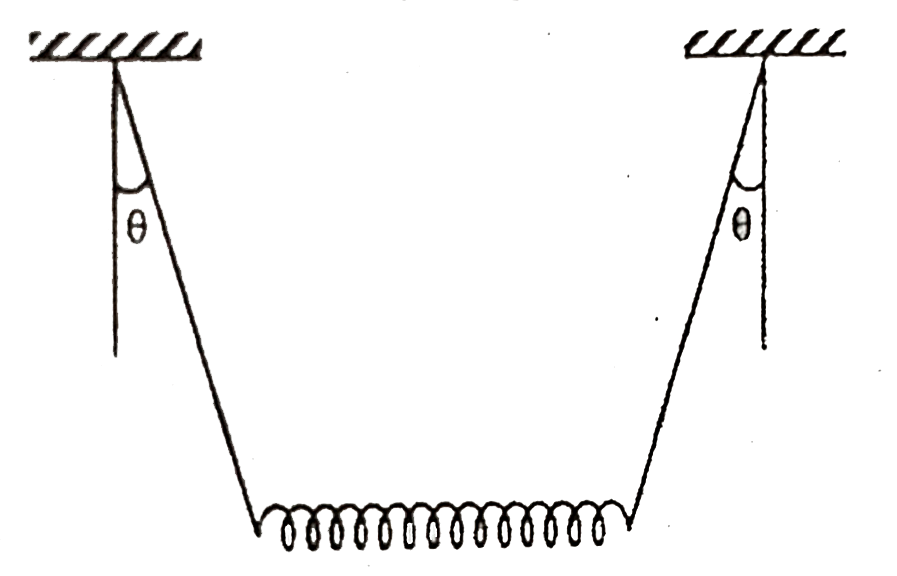 A(W/4k)tanθB(W/2k)tanθC(W/4k)sinθD0
A(W/4k)tanθB(W/2k)tanθC(W/4k)sinθD0
A weight of mass m is suspended from a hinged bracket (Fig.).
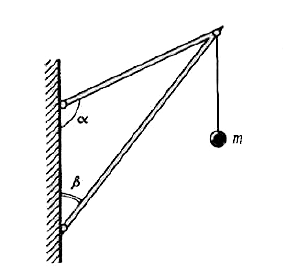
Find the forces in the rods making up the bracket.
View SolutionSolve the same problem for the case of a weight suspended from a thin rod of negligible mass.
View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
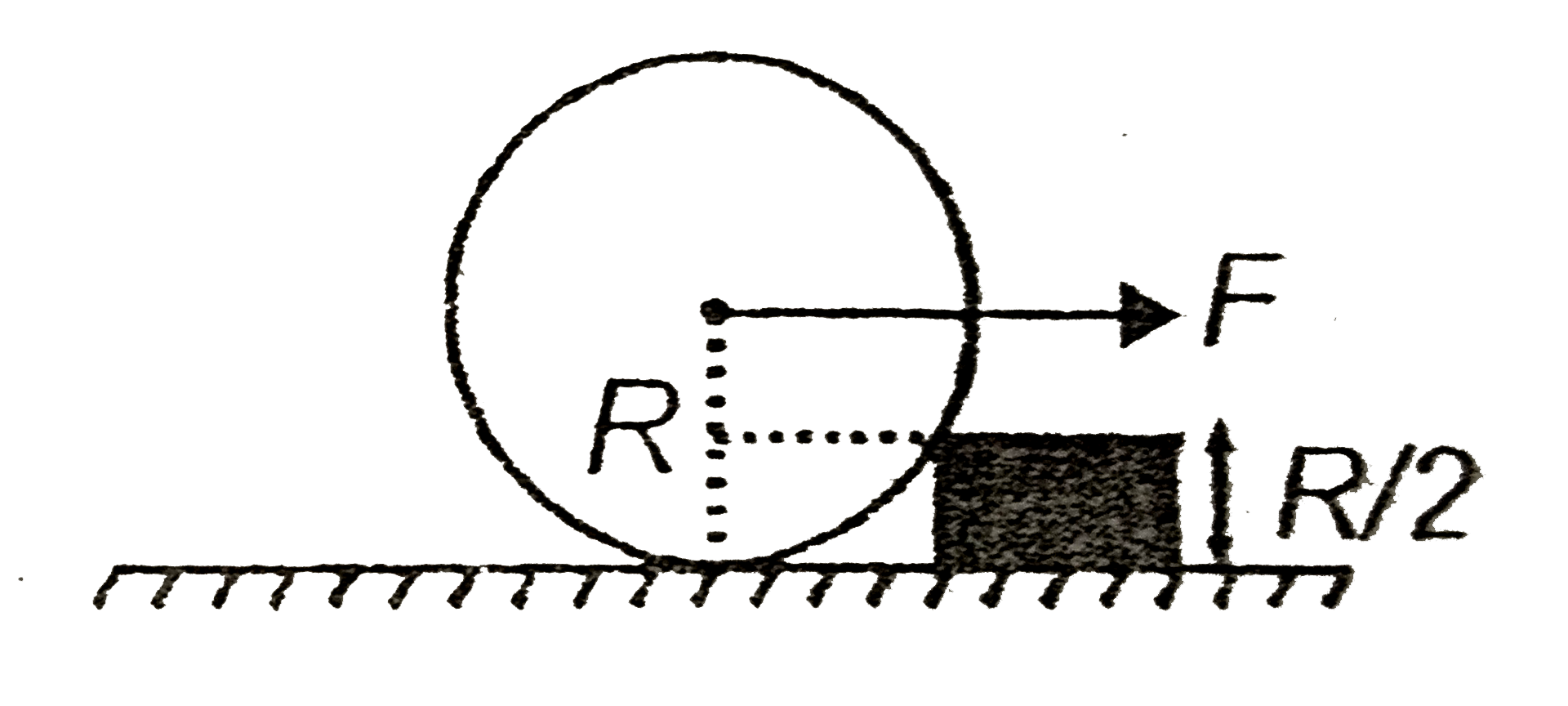
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionOne end of a uniform wire of length L and weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
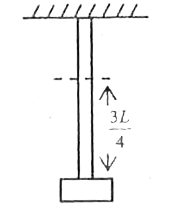
View Solution

