A mass 1 kg is suspended by a thread. It is
(i) lifted up with an acceleration 4.9m/s2
(ii) lowered with an acceleration 4.9m/s2.
The ratio of the tensions is
3:1
1:3
1:2
2:1
The correct Answer is:A
To solve the problem, we need to find the tension in the thread when a mass of 1 kg is lifted and lowered with an acceleration of 4.9 m/s². We will denote the tension when the mass is lifted as T1 and when it is lowered as T2.
1. Identify the forces acting on the mass when lifted:
- When the mass is lifted with an acceleration of 4.9 m/s², the tension (T1) in the thread must overcome both the weight of the mass and provide the additional force due to acceleration.
- The weight of the mass (W) is given by W=mg, where m=1kg and g=9.8m/s2.
- Thus, W=1×9.8=9.8N.
2. Apply Newton's second law for the upward motion:
- According to Newton's second law, the net force (F_net) acting on the mass is equal to the mass times its acceleration (F_net = ma).
- For upward motion, we have:
T1−W=ma
- Substituting the values:
T1−9.8=1×4.9
- Rearranging gives:
T1=9.8+4.9=14.7N
3. Identify the forces acting on the mass when lowered:
- When the mass is lowered with an acceleration of 4.9 m/s², the tension (T2) in the thread must be less than the weight of the mass since it is moving downward.
- The equation for the downward motion is:
W−T2=ma
- Substituting the values:
9.8−T2=1×4.9
- Rearranging gives:
T2=9.8−4.9=4.9N
4. Calculate the ratio of the tensions:
- Now we have T1 and T2:
T1=14.7N,T2=4.9N
- The ratio of the tensions is:
T1T2=14.74.9=3
Final Answer:
The ratio of the tensions T1:T2 is 3:1.
- When the mass is lifted with an acceleration of 4.9 m/s², the tension (T1) in the thread must overcome both the weight of the mass and provide the additional force due to acceleration.
- The weight of the mass (W) is given by W=mg, where m=1kg and g=9.8m/s2.
- Thus, W=1×9.8=9.8N.
- According to Newton's second law, the net force (F_net) acting on the mass is equal to the mass times its acceleration (F_net = ma).
- For upward motion, we have:
T1−W=ma
- Substituting the values:
T1−9.8=1×4.9
- Rearranging gives:
T1=9.8+4.9=14.7N
- When the mass is lowered with an acceleration of 4.9 m/s², the tension (T2) in the thread must be less than the weight of the mass since it is moving downward.
- The equation for the downward motion is:
W−T2=ma
- Substituting the values:
9.8−T2=1×4.9
- Rearranging gives:
T2=9.8−4.9=4.9N
- Now we have T1 and T2:
T1=14.7N,T2=4.9N
- The ratio of the tensions is:
T1T2=14.74.9=3
The ratio of the tensions T1:T2 is 3:1.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Third Law of Motion
24 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Conservation of Linear Momentum and Impulse
27 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
Similar Questions
A mass of 1kg attached to one end of a string is first lifted up with an acceleration 4.9m/s2 and then lowered with same acceleration What is the ratio of tension in string in two cases .
View SolutionA ladder is hanging from ceiling as shown in figure-2.220. Three men of masses 10kg,12kg and 8kg are climbing in such away that man A is going down with an acceleration of 1.6m/s2 and C is rising up with an acceleration of 0.9m/s2 and man B is going up with a constant speed of 0.6m/s.. Find the tension in the string supporting the ladder.
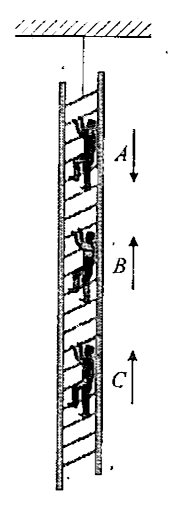
View Solution
Knowledge Check
A mass of 1kg is suspended by a thread. It is
1. lifted up with an accleration 4.9m/s2.
2. lowered with an acceleration 4.9 m/s2.
The ratio of the tensions isA3:1B1:3C1:2D2:1A mass of 1 kg is supended by a string. It is
(i) lifted up with an acceleration 4.9m/s2
(ii) lowered with an acceleration 4.9m/s2
Then the ration of the tension in the string in the two cases isA3:1B1:3C2:1D1:2A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms−2 (ii) lowered with an acceleration of 4.9ms−2. The ratio of tension in the first and second case is
A3:1B1:2C1:3D2:1
A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms−2 (ii) lowered with an acceleration of 4.9 ms−2. The ratio of tension in the first and second case is
View SolutionA mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms−2 (ii) lowered with an acceleration of 4.9ms−2. The ratio of tension in the first and second case is
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
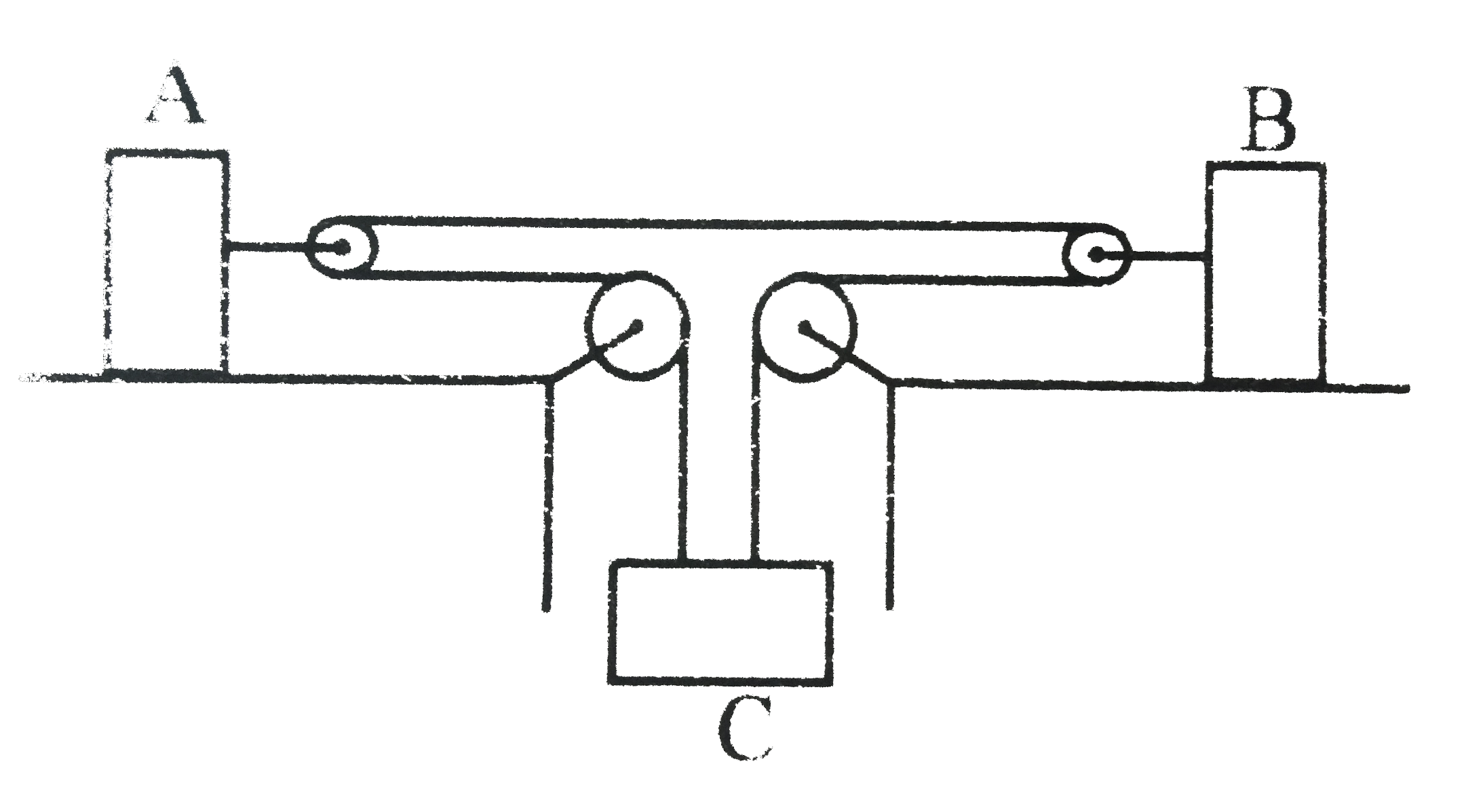
View SolutionA seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8m/s2, its time period is
View SolutionA bob of pendulum of mass 50 g is suspended by string with the roof of an elevator. If the lift is flying with a uniform acceleration of 5ms−2 the tension in the string is (g=10ms−2)
View Solution
